Содержание
- 2. «Высшее назначение математики состоит в том, чтобы находить скрытый порядок в хаосе, который нас окружает.» Н.Винер.
- 3. «... Геометрия владеет двумя сокровищами - теоремой Пифагора и золотым сечением, и если первое из них
- 4. Прямоугольный треугольник с соотношением сторон 3:4:5. Сумма указанных чисел (3+4+5=12) с древних времен использовалась как единица
- 5. Земледелие Отношение 3:4:5 было использовано при построении прямых углов с помощью веревки, размеченной узлами на 3/12
- 6. Моделирование Современный модельный бизнес также использует идеальные пропорции.
- 7. Леонардо Да Винчи ввел термин «золотое сечение», он говорил: «Пусть никто, не будучи математиком, не дерзнет
- 8. Леонардо да Винчи, Рафаэль, Микеланджело и Виньола размышляли о законах «науки пространства», искали тот самый закон
- 9. Золотым сечением и даже «божественной пропорцией» называют такое пропорциональное деление отрезка на неравные части, при котором
- 10. Золотой треугольник А В С Золотым называется такой равнобедренный треугольник, основание и боковая сторона которого находятся
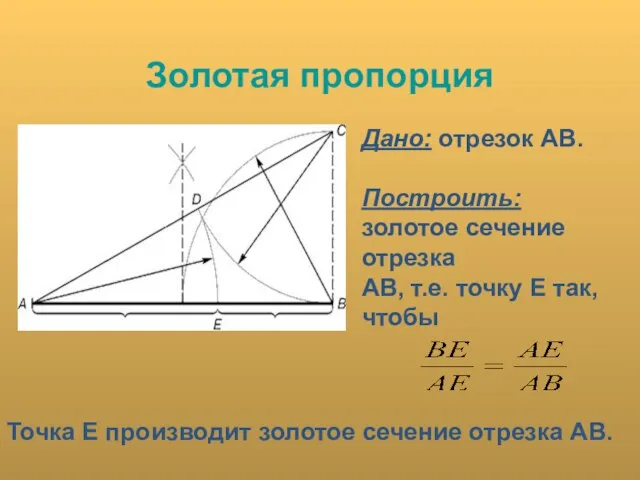
- 11. Золотая пропорция Дано: отрезок АВ. Построить: золотое сечение отрезка АВ, т.е. точку Е так, чтобы .
- 12. Построение. Построим прямоугольный треугольник, у которого один катет в два раза больше другого. Для этого восстановим
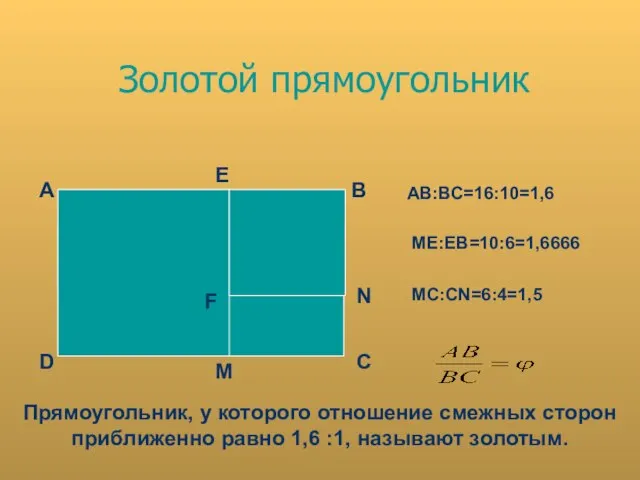
- 13. Золотой прямоугольник F А В С E D N M АВ:ВС=16:10=1,6 ME:EB=10:6=1,6666 MC:СN=6:4=1,5 Прямоугольник, у которого
- 14. Построение. Построить прямоугольник АВСD, стороны которого 16 и 10. Найти отношение сторон. На сторонах прямоугольника построить
- 15. Архитектура
- 16. Леонардо Фибоначчи разгадал тайну числа Ряд чисел выглядит так: 0, 1, 1, 2, 3, 5, 8,
- 17. Построение спирали: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144… Ряд
- 18. Раковина в форме спирали заинтересовала и Архимеда: он выяснил, что увеличение длины завитков раковины – постоянная
- 19. С помощью числового ряда Фибоначчи описывается устройство Галактик, волн
- 20. Млечный путь - так называется наша галактика В самом центре есть большая чёрная дыра, но это
- 21. Последовательность Фибоначчи, проиллюстрированная природой.
- 22. Семена в подсолнухе, в шишке располагаются так же в виде спирали. Пауки плетут свою сеть и
- 23. Все живое подчиняется божественному закону
- 24. И нерукотворные творения
- 26. Скачать презентацию





















 Смежные и вертикальные углы
Смежные и вертикальные углы Теорема Пифагора задачи
Теорема Пифагора задачи Изображение пространственных фигур Мячина Екатерина Колдаева Есения 11 Г класс
Изображение пространственных фигур Мячина Екатерина Колдаева Есения 11 Г класс ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ Петрова Людмила Анатольевна, учитель математики, г.Санкт-Петербург, лицей № 1
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ Петрова Людмила Анатольевна, учитель математики, г.Санкт-Петербург, лицей № 1 Определение и признак перпендикулярности плоскостей
Определение и признак перпендикулярности плоскостей Прямоугольный параллелепипед
Прямоугольный параллелепипед Медиана. Биссектриса. Высота. «Элементы треугольника» Выполнил работу ученик 10 класса
Медиана. Биссектриса. Высота. «Элементы треугольника» Выполнил работу ученик 10 класса 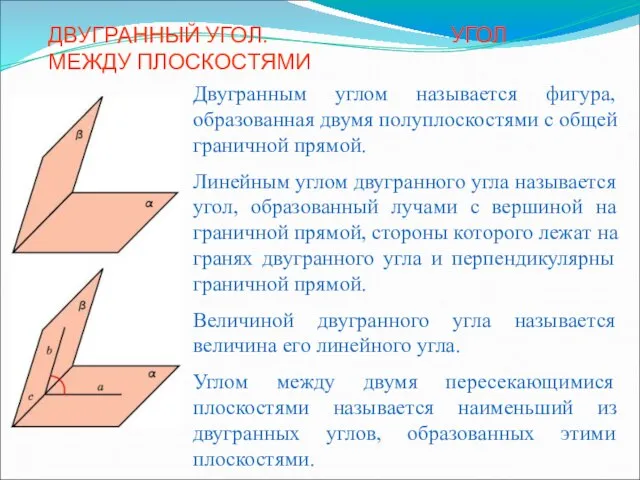 Двугранный угол. Угол между плоскостями
Двугранный угол. Угол между плоскостями Вычисление площадей геометрических фигур
Вычисление площадей геометрических фигур Развёртка куба
Развёртка куба Бумажные складные модели и их использование на уроках геометрии в 10 классе
Бумажные складные модели и их использование на уроках геометрии в 10 классе Применение параллелограмма
Применение параллелограмма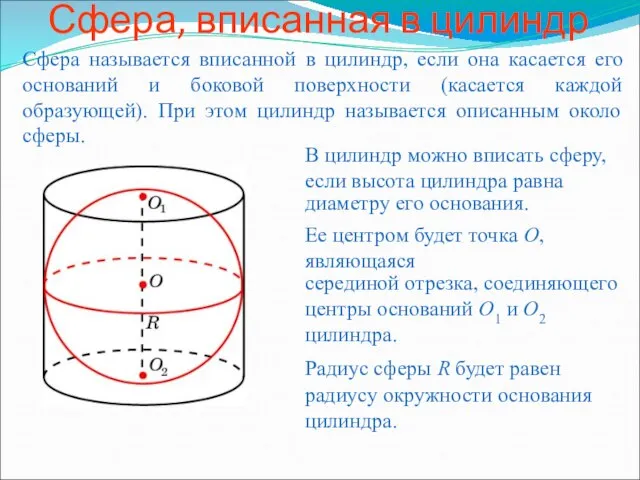 Сфера, вписанная в цилиндр
Сфера, вписанная в цилиндр Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________
Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________ Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год.
Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год. Медиана, биссектриса и высота треугольника
Медиана, биссектриса и высота треугольника Музей истории четырёхугольников
Музей истории четырёхугольников Гипотеза пуанкаре и терстона
Гипотеза пуанкаре и терстона Пирамиды
Пирамиды Лабораторный практикум по геометрии 7 класс
Лабораторный практикум по геометрии 7 класс Прямоугольный параллелепипед (5 класс)
Прямоугольный параллелепипед (5 класс) Путешествие в страну Геометрия
Путешествие в страну Геометрия Решение задач на нахождение периметра и площади
Решение задач на нахождение периметра и площади Цилиндр. Конус. Шар
Цилиндр. Конус. Шар Объём пирамиды
Объём пирамиды Решение задач на применение аксиом стереометрии и их следствий
Решение задач на применение аксиом стереометрии и их следствий Классическое определение вероятности. Комбинаторные методы решения задач
Классическое определение вероятности. Комбинаторные методы решения задач Луч и угол (7 класс)
Луч и угол (7 класс)