Содержание
- 2. Цели: познакомиться с историей развития решения задачи деления угла на три равные части; поиск решения задачи
- 3. Краткое содержание: Вступление; Постановка проблемы; Исторические сведения; Методы доказательства; Решение задачи о трисекции угла циркулем и
- 4. Вступление. Задачи на геометрические построения – одни из самых популярных в школьной математике. История геометрических построений
- 5. Постановка проблемы. С глубокой древности известна одна из знаменитых задач древности – задача о трисекции угла.
- 6. Исторические сведения. Платон, живший в 428 – 328 годах до нашей эры, считается одним из величайших
- 7. Архимед. Архимед (?287-212 гг. до нашей эры) родился в городе Сиракузы на острове Сицилия. Он автор
- 8. Методы доказательства. Существуют различные способы построения трисектрисы угла: При помощи циркуля и линейки без засечек (трисекция
- 9. Решение задачи о трисекции угла циркулем и линейкой.
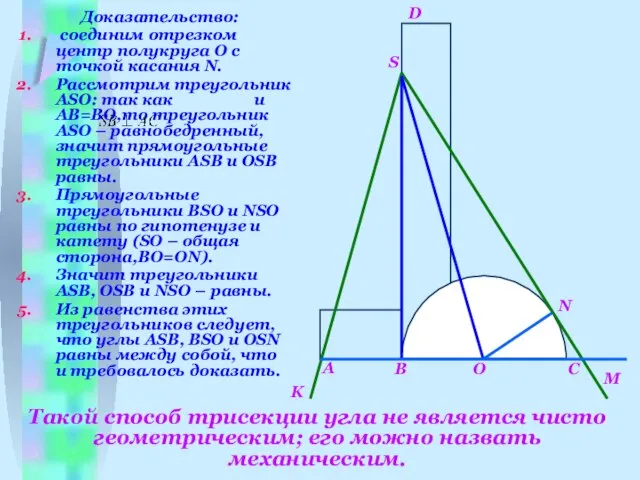
- 10. Простейший трисектор. На сегодняшний день придумано много механических способов для построения трисектрисы угла. Такие приборы называются
- 11. Такой способ трисекции угла не является чисто геометрическим; его можно назвать механическим.
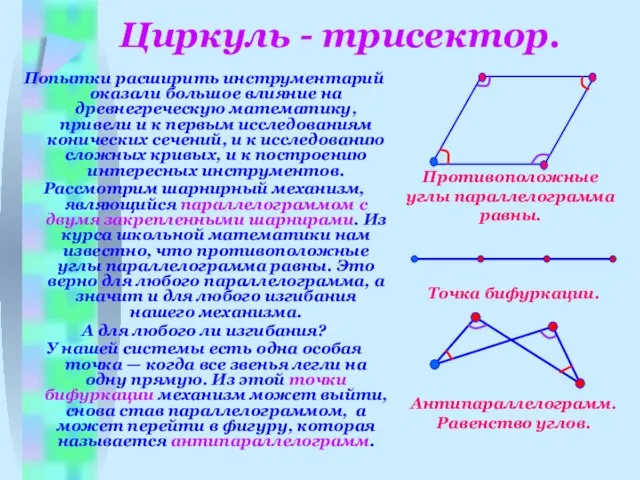
- 12. Циркуль - трисектор. Попытки расширить инструментарий оказали большое влияние на древнегреческую математику, привели и к первым
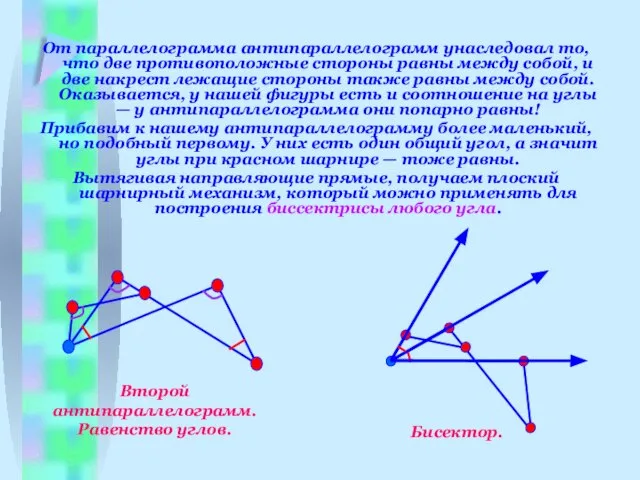
- 13. От параллелограмма антипараллелограмм унаследовал то, что две противоположные стороны равны между собой, и две накрест лежащие
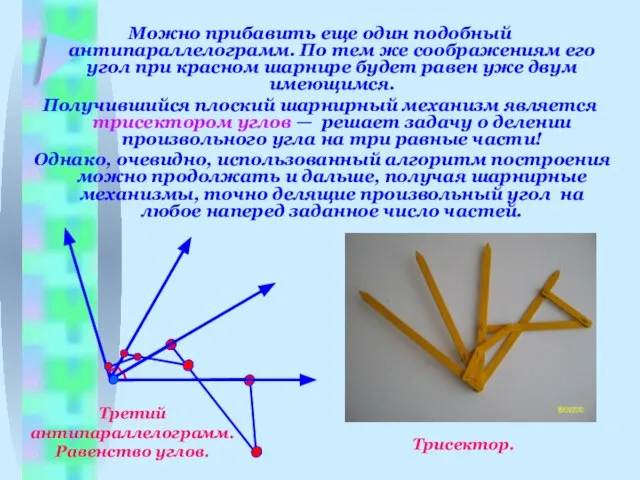
- 14. Можно прибавить еще один подобный антипараллелограмм. По тем же соображениям его угол при красном шарнире будет
- 15. Практическое применение циркуля- трисектора.
- 16. Вывод При выяснении возможности планиметрической задачи на построение пользуются следующим критерием: построение отрезка циркулем и линейкой
- 18. Скачать презентацию











 Фракталы – геометрия природы
Фракталы – геометрия природы Простейшие задачи в координатах
Простейшие задачи в координатах Длина окружности
Длина окружности Чудеса симметрии
Чудеса симметрии Взаимное положение прямых Начертательная геометрия 11 класс
Взаимное положение прямых Начертательная геометрия 11 класс Гладунец Ирина Владимировна Учитель математики МБОУ гимназии №1 г.Лебедянь Липецкой области
Гладунец Ирина Владимировна Учитель математики МБОУ гимназии №1 г.Лебедянь Липецкой области ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ Петрова Людмила Анатольевна, учитель математики, г.Санкт-Петербург, лицей № 1
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ Петрова Людмила Анатольевна, учитель математики, г.Санкт-Петербург, лицей № 1 Геометрия крестово-купольного храма
Геометрия крестово-купольного храма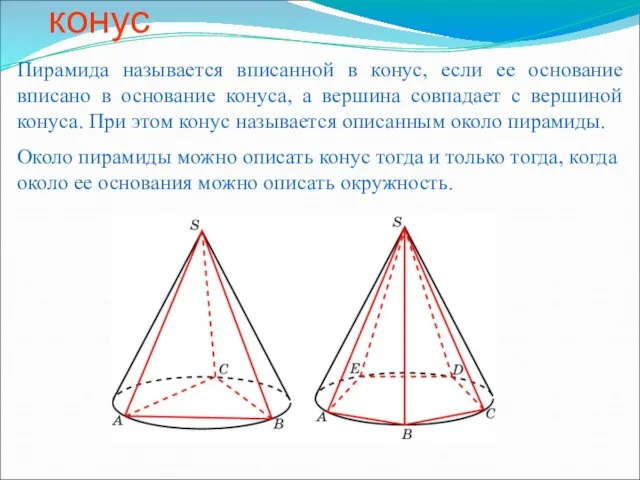 Пирамида, вписанная в конус
Пирамида, вписанная в конус Многообразие многоугольников
Многообразие многоугольников Площади плоских геометрических фигур
Площади плоских геометрических фигур От сферы к плоскости
От сферы к плоскости Многогранник
Многогранник Флексагоны флексоры
Флексагоны флексоры Теорема Пифагора. Приминение
Теорема Пифагора. Приминение Логические законы и правила
Логические законы и правила Свойство точек биссектрисы угла.
Свойство точек биссектрисы угла. Красота, гармония, симметрия
Красота, гармония, симметрия Геометрические задачи на экстремум
Геометрические задачи на экстремум Симметрия
Симметрия Объемные тела. Пирамиды
Объемные тела. Пирамиды Моделирование и формализация
Моделирование и формализация Развёртка куба
Развёртка куба Осевая и центральная симметрии
Осевая и центральная симметрии Сумма углов в треугольнике
Сумма углов в треугольнике Измерение длин отрезков
Измерение длин отрезков Смежные и вертикальные углы
Смежные и вертикальные углы Решение задач на нахождение периметра и площади
Решение задач на нахождение периметра и площади