Слайд 3Правильные фигуры и тела.
Геометрия - раздел математики, изучающий пространственные отношения и формы.

Пусть дан в окружность равнобедренный треугольник ACD, у которого угол C равен углу D и равный двум углам A. Проведем биссектрисы CE и CB углов Си D соответственно. Тогда угол А будет равен всем четырем полученным углам, а, следовательно, будут равны соответствующие им дуги и стягивающие их хорды, то есть AB=BC=CD=DE=EA. Итак, вписанный в окружность пятиугольник ABCDE будет равносторонним. Поскольку угол шесть равен углу два и угол семь равен углу пять как углы, опирающиеся на одинаковые дуги AE и AB соответственно, то все углы 1-7 будут равными и, следовательно, каждый угол пятиугольника ABCDE будет составлен из трех равных углов, то есть угол A равен углу B и равен углу C углу D и углу E. Также все эти углы равны трем углам CAD. Таким образом, построенный пятиугольник является равносторонним и равноугольным, то есть правильным.
Слайд 4Правильные многогранники и научные факты.
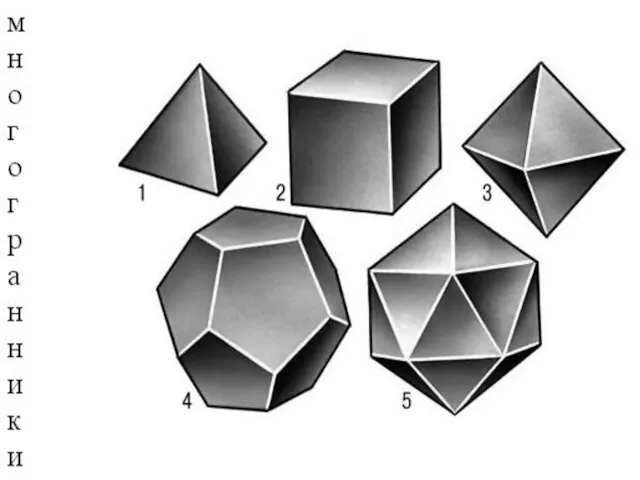
Правильных многогранников всего ПЯТЬ! Сама природа подсказала пифагорейцам

форму правильных тел: кристаллы поваренной соли имеют форму куба, кристаллы квасцов октаэдра, а кристаллы пирита – додекаэдра.
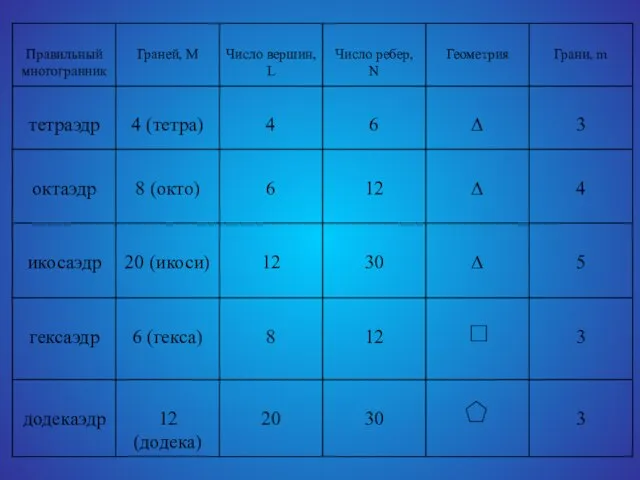
Однако важнейшее свойство выпуклых многогранников было установлено лишь в середине 18 века теоремой Эйлера: во всяком выпуклом многограннике число вершин (L) плюс число граней (M) минус число ребер (N) есть величина постоянная равная двум:
L+M-N=2
Слайд 6Научные фантазии и правильные многогранники.
МНОГОГРАННИК - геометрическое тело, ограниченное со всех сторон

плоскими многоугольниками, называемыми гранями. Стороны граней называются ребрами многогранника, а концы ребер - вершинами многогранника. Ни одни геометрические тела не обладают таким совершенством и красотой, как правильные многогранники. "Правильных многогранников вызывающе мало, - написал когда-то Л. Кэрролл, - но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук".
Слайд 7Тетраэдр.
Тетраэдр-четырехгранник, все грани которого треугольники, т.е. треугольная пирамида; правильный тетраэдр ограничен четырьмя

равносторонними треугольниками; один из пяти правильных многоугольников.
Слайд 8Куб.
Куб или правильный гексаэдр - правильная четырехугольная призма с равными ребрами, ограниченная

шестью квадратами.
Слайд 9Октаэдр.
Октаэдр-восьмигранник; тело, ограниченное восемью треугольниками; правильный октаэдр ограничен восемью равносторонними треугольниками; один

из пяти правильных многогранников.
Слайд 10Додекаэдр.
Додекаэдр-двенадцатигранник, тело, ограниченное двенадцатью многоугольниками; правильный пятиугольник; один из пяти правильных многогранников.

Слайд 11Икосаэдр.
Икосаэдр-двадцатигранник, тело, ограниченное двадцатью многоугольниками; правильный икосаэдр ограничен двадцатью равносторонними треугольниками; один

из пяти правильных многогранников.
Слайд 13Мистика ПЯТИ правильных многогранников.
Платон считал, что мир строится из четырех "стихий" -

огня, земли, воздуха и воды, а атомы этих «стихий" имеют форму четырех правильных многогранников. Итак, тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у разгоревшегося пламени; икосаэдр – как самый обтекаемый – воду; куб – самая устойчивая из фигур – землю, а октаэдр – воздух. В наше время эту систему можно сравнить с четырьмя состояниями вещества – твердым, жидким, газообразным и плазменным. Пятый многогранник - додекаэдр - воплощал в себе «все сущее", символизировал весь мир и почитался главнейшим.
Слайд 14Теории о кристаллах.
Кристаллы правильной геометрической формы встречаются в природе редко. Совместное действие

таких неблагоприятных факторов, как колебания температуры, тесное окружение соседними твердыми телами, не позволяют растущему кристаллу приобрести характерную для него форму. Кроме того, значительная часть кристаллов, имевших в далеком прошлом совершенную огранку, успела утратить ее под действием воды, ветра, трения о другие твердые тела. Так, многие округлые прозрачные зерна, которые можно найти в прибрежном песке, являются кристаллами кварца, лишившимися граней в результате длительного трения друг о друга.
Слайд 15Гипотеза о ядре Земли.
Идеи Пифагора, Платона, Кеплера о связи правильных многогранников с

гармоничным устройством мира и в наше время нашли свое продолжение в интересной научной гипотезе, которую вначале 80-х гг. высказали московские инженеры В. Марков и В.Морозов. Они считают, что ядро Земли имеют форму и свойства растущего кристалла. Оказывающего воздействие на развитие всех природных процессов, идущих на планете. Лучи этого кристалла, а точнее, его силовое поле, обусловливают икосаэдро-додекаэдровую структуру Земли. Она появляется в том, что в земной коре как бы поступают проекции вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра.
Многие залежи полезных ископаемых тянутся вдоль икосаэдро-додекаэдровой сетки; 62 вершины и середины ребер многогранников, называемых авторами узлами, обладают рядом специфических свойств, позволяющих объяснить некоторые непонятные явления. Здесь располагаются очаги древнейших культур и цивилизаций: Перу, Северная Монголия, Гаити и другие. В этих точках наблюдаются максимумы и минимумы атмосферного давления, гигантские завихрения Мирового океана. В этих узлах находятся озеро Лох-Несс, Бермудский треугольник. Дальнейшие исследования Земли, возможно, определяет отношение к этой научной гипотезе, в которой, как видно, правильные многогранники занимают важное место.
Слайд 16Правильные многогранники в природе.
Правильные многогранники встречаются и в живой природе. Например, скелет

одноклеточного организма феодарии по форме напоминает икосаэдр.
Интересно, что икосаэдр оказался в центре внимания биологов в их спорах относительно формы некоторых вирусов. Вирус не может быть совершенно круглым, как считалось раньше. Для того чтобы определить его форму, брали разные многогранники, направляли на них свет под теми же углами, что и поток атома на вирус. Оказалось, что только один многогранник дает точно такую же тень - икосаэдр.
Правильные многогранники - самые выгодные фигуры. И природа этим широко пользуется. Подтверждением того служит форма некоторых кристаллов. Взять хоть бы поваренную соль, без которой мы не можем обойтись. Известно, что она хорошо растворима в воде, служит проводником электрического тока. А кристаллы поваренной соли (NaCl) имеют форму куба.
При производстве алюминия пользуются алюминиево-кальциевыми квасцами (К[АI(SО4)2] . 12Н20), монокристалл который имеет форму правильного октаэдра.
Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана (FeS). Кристаллы этого химического вещества имеют форму додекаэдра.
Итак, благодаря правильным многогранникам открываются не только удивительные свойства геометрических фигур, но и пути познания природной гармонии.
Слайд 17Практикум.
Геометрические способности пчел проявляются при построении сот. Если разрезать пчелиные соты плоскостью,

перпендикулярной их ребрам, то станет видна сеть равных друг другу правильных шестиугольников, уложенных в виде паркета. Возникает вопрос: "Почему пчелы строят соты именно так: они предпочли сеть правильных шестиугольников, а не правильных треугольников или квадратов, ведь их, кажется, проще сконструировать?"
Чтобы ответить на этот вопрос, необходимо предварительно выяснить, какими правильными многоугольниками можно заполнить плоскость так, чтобы не было пропусков, т.е. уложить их в виде паркета.
Такими многоугольниками могут быть только правильные треугольники, квадраты и правильные шестиугольники.
Слайд 18Для того, чтобы выяснить, почему пчела строит соты, перпендикулярное сечение которых есть

правильный шестиугольник, а не правильный треугольник или квадрат, решим для этого приведенную нижу задачу.
Задача. Даны три равновеликие друг другу фигуры - правильный треугольник, квадрат и правильный шестиугольник. Какая из данных фигур имеет наименьший периметр?
Мы видим, что из трех правильных многоугольников с одинаковой площадью наименьший периметр имеет правильный шестиугольник, мудрые пчелы экономят воск и время для построения сот.
Слайд 19Заключение.
Правильные многогранники на протяжении всей истории человечества не переставали восхищать пытливые умы

симметрией, мудростью и совершенством своих форм. Леонардо да Винчи любил мастерить каркасы правильных тел и преподносить их в дар знатным особам, возможно, пытаясь таким образом приобщить сильных мира сего к философским размышлениям о красоте вечных истин.
Но на пяти правильных телах история многогранников не остановилась. Вслед за правильными телами Платона были открыты полуправильные тела Архимеда, грани которых составлены из правильных равных многоугольников несколько видов, причем в каждой вершине сходится одно и то же число одинаковых граней в одинаковом порядке и многогранные углы при вершинах равны. Заметим, что тела Архимеда могут быть получены из соответствующих тел Платона снятием равных фасок. Тел Архимеда всего 13. Любопытно, что во второй половине ХХ в. было обнаружено еще одно тело Архимеда псевдоромбокубооктаэдр, которое не может быть получено путем однотипных усечением тела Платона и поэтому в течение 2000 лет оставалось незамеченным.
И все-таки знакомство с многогранниками я советую начать с «Начал» Евклида, ибо, как сказал Альберт Эйнштейн, «Тот не рожден для теоретических исследований. Кто в молодости не восхищался этим творением».















 Медиана, биссектриса и высота треугольника
Медиана, биссектриса и высота треугольника Бумажные складные модели и их использование на уроках геометрии в 10 классе
Бумажные складные модели и их использование на уроках геометрии в 10 классе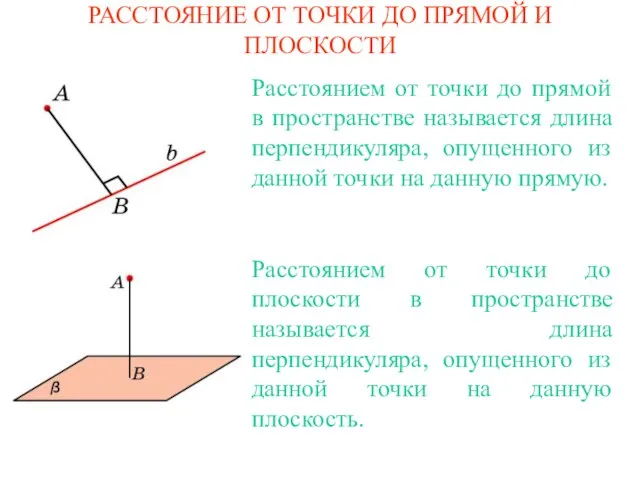 Расстояние от точки до прямой и плоскости
Расстояние от точки до прямой и плоскости Цилиндр. Конус. Шар
Цилиндр. Конус. Шар Признаки равенства треугольников
Признаки равенства треугольников Медианы, биссектрисы и высоты треугольника
Медианы, биссектрисы и высоты треугольника Фракталы и их применение в наши дни
Фракталы и их применение в наши дни Определение синуса, косинуса, тангенса и котангенса
Определение синуса, косинуса, тангенса и котангенса ВПИСАННЫЕ И ОПИСАННЫЕ ТРЕУГОЛЬНИКИ
ВПИСАННЫЕ И ОПИСАННЫЕ ТРЕУГОЛЬНИКИ Сумма углов треугольника 5 класс - презентация_
Сумма углов треугольника 5 класс - презентация_ Начертательная геометрия
Начертательная геометрия Графическое решение квадратных уравнений
Графическое решение квадратных уравнений Площадь прямоугольника
Площадь прямоугольника Вычисление угла между прямыми и плоскостями
Вычисление угла между прямыми и плоскостями Взаимное расположение прямых и плоскостей в пространстве
Взаимное расположение прямых и плоскостей в пространстве Свойство точек биссектрисы угла.
Свойство точек биссектрисы угла. Площадь трапеции
Площадь трапеции Доклад о «Сфере и шаре»
Доклад о «Сфере и шаре» Угол между плоскостями
Угол между плоскостями Геометрия крестово-купольного храма
Геометрия крестово-купольного храма ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности Площади плоских геометрических фигур
Площади плоских геометрических фигур Многогранники
Многогранники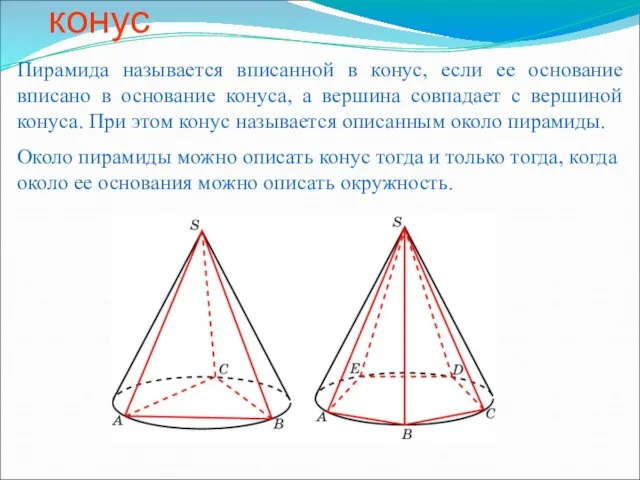 Пирамида, вписанная в конус
Пирамида, вписанная в конус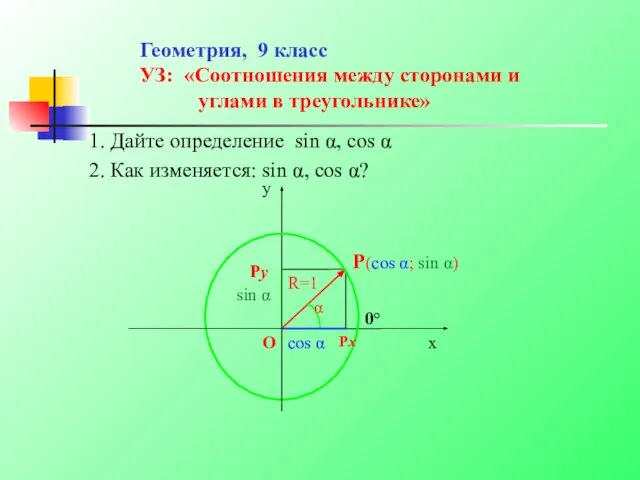 Соотношения между сторонами и углами в треугольнике
Соотношения между сторонами и углами в треугольнике Анализ геометрической формы предмета
Анализ геометрической формы предмета Золотое сечение в геометрии - презентация по Геометрии_
Золотое сечение в геометрии - презентация по Геометрии_ Теорема косинусов
Теорема косинусов