Содержание
Слайд 2Прямая, проходящая через точку М0 (х0; f(х0)), с отрезком которой почти сливается
Прямая, проходящая через точку М0 (х0; f(х0)), с отрезком которой почти сливается
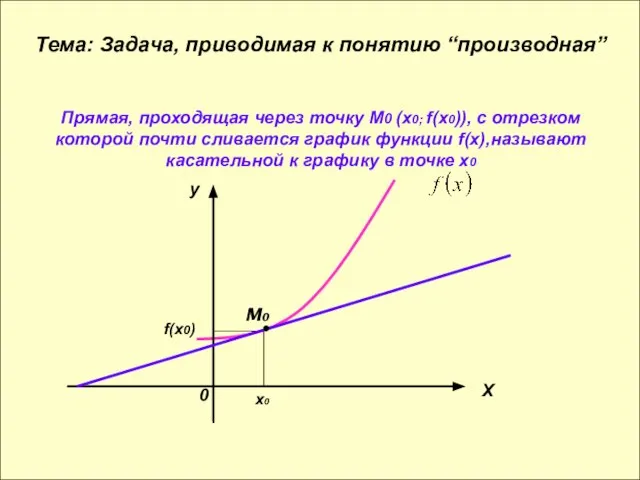
график функции f(х),называют касательной к графику в точке х0
x0
f(x0)
M0
X
y
Тема: Задача, приводимая к понятию “производная”
0
- Предыдущая
Перпендикулярные прямые в пространствеСледующая -
Длина окружности Упражнения со спичками (занятие 9)
Упражнения со спичками (занятие 9) Трехгранный угол
Трехгранный угол Описанная окружность
Описанная окружность ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности Решение задач на применение аксиом стереометрии и их следствий
Решение задач на применение аксиом стереометрии и их следствий Симметрия. Осевая и центральная симметрии
Симметрия. Осевая и центральная симметрии Резьба. Крепёжные изделия
Резьба. Крепёжные изделия Сопряжение. Геометрические построения - презентация по Геометрии_
Сопряжение. Геометрические построения - презентация по Геометрии_ Презентация на тему: Сечение
Презентация на тему: Сечение ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ
ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ Основные свойства простейших геометрических фигур
Основные свойства простейших геометрических фигур Решение задач по курсу геометрии
Решение задач по курсу геометрии Путешествие в страну Геометрия
Путешествие в страну Геометрия Скалярное произведение в координатах
Скалярное произведение в координатах Треугольники. Сумма углов треугольника - презентация по Геометрии_
Треугольники. Сумма углов треугольника - презентация по Геометрии_ Орнамент - математическое воплощение красоты
Орнамент - математическое воплощение красоты Развёртка куба
Развёртка куба Замечательные кривые
Замечательные кривые Свойство скрещивающихся рёбер правильной треугольной пирамиды
Свойство скрещивающихся рёбер правильной треугольной пирамиды Сумма углов в треугольнике
Сумма углов в треугольнике Окружности
Окружности Задачи на построение сечений
Задачи на построение сечений Геометрия крестово-купольного храма
Геометрия крестово-купольного храма Шар
Шар Решение задач на применение первого признака равенства треугольников МОУ ООШ Д. Старое Мелково Учитель: Костик Инна Станиславовн
Решение задач на применение первого признака равенства треугольников МОУ ООШ Д. Старое Мелково Учитель: Костик Инна Станиславовн Равнобедренная трапеция
Равнобедренная трапеция Многогранник
Многогранник