Содержание
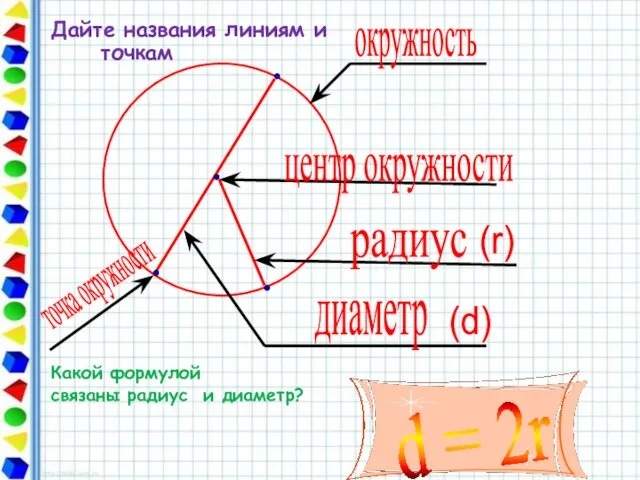
- 2. Дайте названия линиям и точкам Какой формулой связаны радиус и диаметр? ??? окружность ??? центр окружности
- 3. Длину отрезка можно измерить с помощью линейки, длину ломаной можно найти, измерив её звенья и сложив
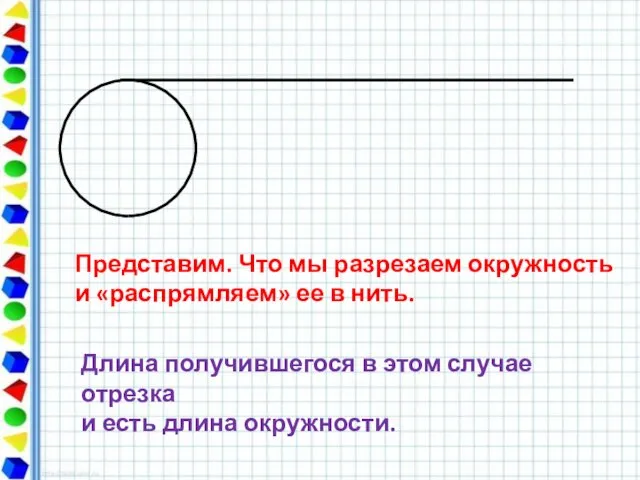
- 4. Представим. Что мы разрезаем окружность и «распрямляем» ее в нить. Длина получившегося в этом случае отрезка
- 5. Длина окружности обозначается буквой C.
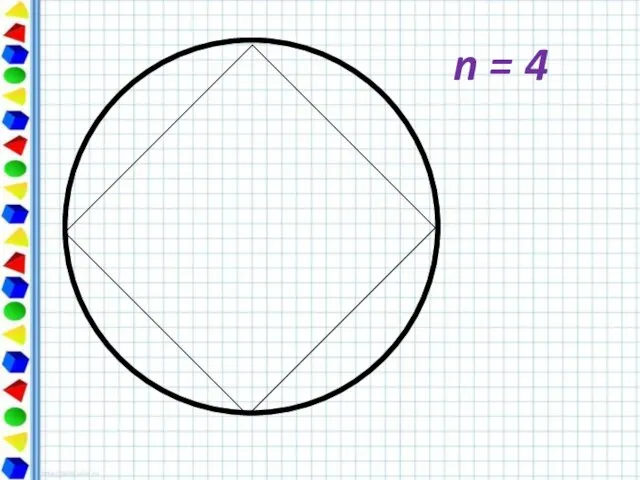
- 6. n = 4
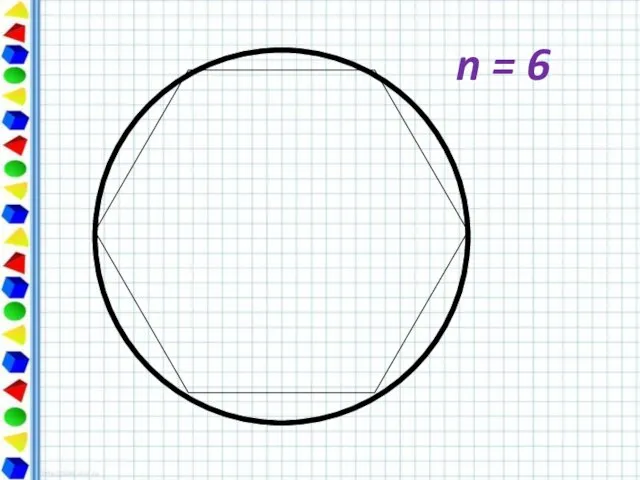
- 7. n = 6
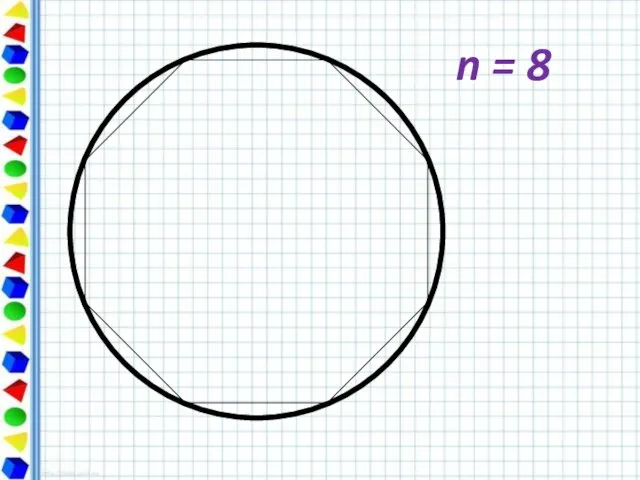
- 8. n = 8
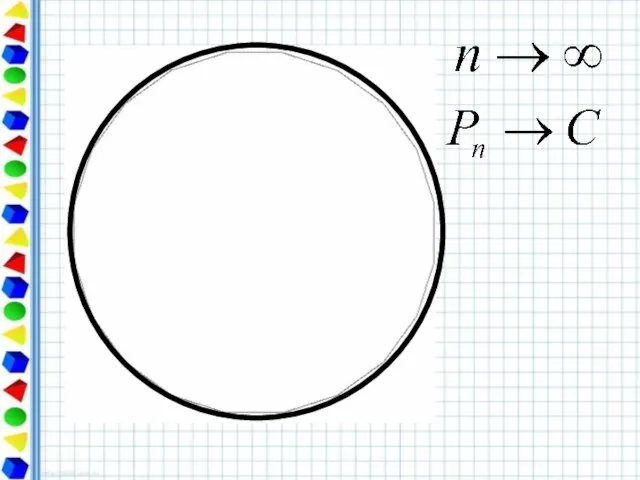
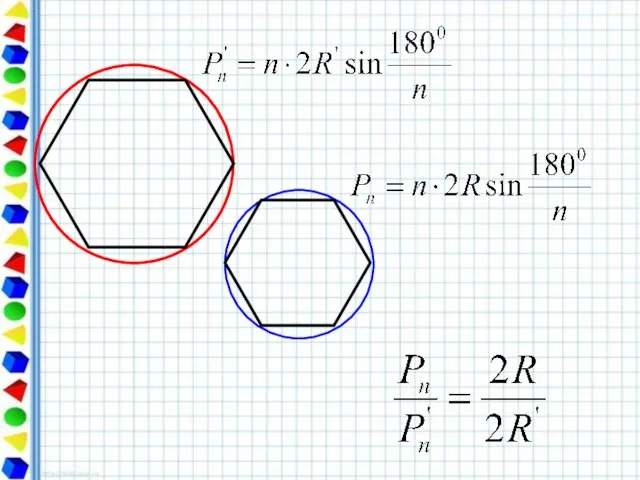
- 10. Периметр любого вписанного в окружность многоугольника является приближённым значением длины окружности. При увеличении числа сторон правильный
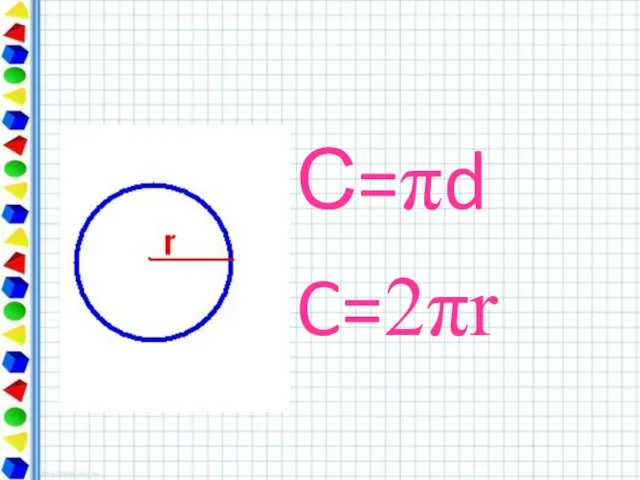
- 13. С=πd C=2πr
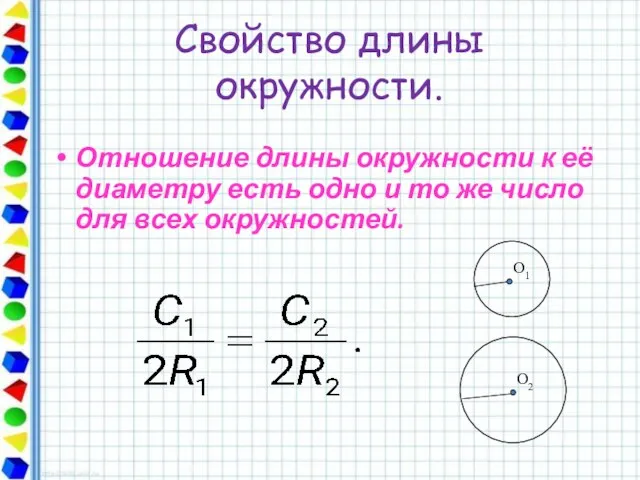
- 14. O1 Свойство длины окружности. Отношение длины окружности к её диаметру есть одно и то же число
- 15. Число Π
- 16. ≈3,14159265358 9793238462643… π≈3,14 = 22 7
- 17. Обозначение числа происходит от первой буквы греческого слова периферия, что означает "окружность". Чаще всего используется его
- 18. А есть и стихотворения, например: Чтобы нам не ошибаться, надо правильно прочесть: три, четырнадцать, пятнадцать, девяносто
- 19. Из древнеегипетских и вавилонских источников известно, что потребности того времени вполне удовлетворяло число, равное трем. Позже
- 20. Вычислением числа занимались в более поздние века многие знаменитые математики. Французский математик Франсуа Виет вычислил
- 21. Мировой рекорд по запоминанию знаков числа П принадлежит японцу Акира Харагути (Akira Haraguchi). Он запомнил число
- 22. 510 знаков после запятой: π ≈ 3,141 592 653 589 793 238 462 643 383 279
- 23. Сто миллионов знаков после запятой 3,1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811745028410270193852110555964462294895493038196442881097566593344612847564823378678316527120190914564856692346034861045432648213393607260249141273724587006606315588174881520920962829254091715364367892590360011330530548820466521384146951941511609433057270365759591953092186117381932611793105118548074462379962749567351885752724891227938183011949129833673362440656643086021394946395224731907021798609437027705392171762931767523846748184676694051320005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235420199561121290219608640344181598136297747713099605187072113499999983729780499510597317328160963185950244594553469083026425223082533446850352619311881710100031378387528865875332083814206171776691473035982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164201989380952572010654858632788659361533818279682303019520353018529689957736225994138912497217752834791315155748572424541506959508295331168617278558890750983817546374649393192550604009277016711390098488240128583616035637076601047101819429555961989467678374494482553797747268471040475346462080466842590694912933136770289891521047521620569660240580381501935112533824300355876402474964732639141992726042699227967823547816360093417216412199245863150302861829745557067498385054945885869269956909272107975093029553211653449872027559602364806654991198818347977535663698074265425278625518184175746728909777727938000816470600161452491921732172147723501414419735685481613611573525521334757418494684385233239073941433345477624168625189835694855620992192221842725502542568876717904946016534668049886272327917860857843838279679766814541009538837863609506800642251252051173929848960841284886269456042419652850222106611863067442786220391949450471237137869609563643719172874677646575739624138908658326459958133904780275900994657640789512694683983525957098258226205224894077267194782684826014769909026401363944374553050682034962524517493996514314298091906592509372216964615157098583874105978859597729754989301617539284681382686838689427741559918559252459539594310499725246808459872736446958486538367362226260991246080512438843904512441365497627807977156914359977001296160894416948685558484063534220722258284886481584560285060168427394522674676788952521385225499546667278239864565961163548862305774564980355936345681743241125150760694794510965960940252288797108931456691368672287489405601015033086179286809208747609178249385890097149096759852613655497818931297848216829989487226588048575640142704775551323796414515237462343645428584447952658678210511413547357395231134271661021359695362314429524849371871101457654035902799344037420073105785390621983874478084784896833214457138687519435064302184531910484810053706146806749192781911979399520614196634287544406437451237181921799983910159195618146751426912397489409071864942319615679452080951465502252316038819301420937621378559566389377870830390697920773467221825625996615014215030680384477345492026054146659252014974428507325186660021324340881907104863317346496514539057962685610055081066587969981635747363840525714591028970641401109712062804390397595156771577004203378699360072305587631763594218731251471205329281918261861258673215791984148488291644706095752706957220917567116722910981690915280173506712748583222871835209353965725121083579151369882091444210067510334671103141267111369908658516398315019701651511685171437657618351556508849099898599823873455283316355076479185358932261854896321329330898570642046752590709154814165498594616371802709819943099244889575712828905923233260972997120844335732654893823911932597463667305836041428138830320382490375898524374417029132765618093773444030707469211201913020330380197621101100449293215160842444859637669838952286847831235526582131449576857262433441893039686426243410773226978028073189154411010446823252716201052652272111660396
- 24. Теперь известно, что число иррациональное, может быть представлено в виде бесконечной непериодической десятичной дроби. С
- 25. Существует даже праздник числа П! Неофициальный праздник «День числа Пи» отмечается 14 марта, которое в американском
- 26. В Сиэтле (США) существует памятник числу П, который находится на ступенях перед зданием Музея искусств
- 27. Задачи по теме «Длина окружности» Порешаем!!!
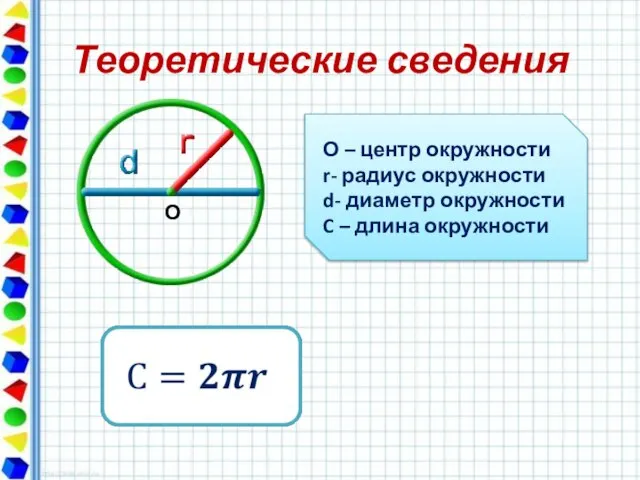
- 28. Теоретические сведения О О – центр окружности r- радиус окружности d- диаметр окружности C – длина
- 29. Задача: 1) вычислить длину окружности, если ее диаметр равен 6 см 2) вычислить длину окружности, если
- 30. Решение: 1) D=6 см С= 3,14• 6 =18,84 (см) Ответ: длина окружности 18,84 см С =
- 31. Задача: Длина окружности цирковой арены равна 41 м. Найдите диаметр арены цирка С = П D
- 32. Решение: С = П D С=41 м 41 = 3,14•D D = 41 : 3,14 D
- 33. Диаметр d= 5м О ? Длина окружности – С Цветочная клумба имеет форму круга, диаметр которого
- 34. С = 3,14•5=15,7 (м) Ответ: длина полосы дерна равна 15,7 м С = П D Решение:
- 35. Ныне самым старым деревом является гигантский кипарис, который растет в одном из сел Южной Мексики. Диаметр
- 36. Решите задачу У лукоморья дуб зелёный; Златая цепь на дубе том: И днём и ночью кот
- 37. Решение 0,35 * 6 = 2,1 (км) прошел кот за 6 часов 2,1 : 70 =
- 38. Отлитый в 1735 г. Царь колокол, хранящийся в Московском Кремле, имеет диаметр основания 6,6 м. Вычислите
- 39. Решите задачу Пришкольная площадка имеет форму квадрата периметром 96 м. посередине ее стоит Вовочка и крутит
- 40. Решите задачу Наконец и в путь обратный Со своею силой ратной И с девицей молодой Царь
- 41. Решите задачу На побережье Средиземного моря растет интересное растение- так называемый стреляющий огурец. Чтобы обеспечить себе
- 42. Задача (О Тунгусском метеорите, 1908 г.) Диаметр опалённой площади тайги от взрыва Тунгусского метеорита равен примерно
- 43. Древнегреческий математик Архимед установил, что длина окружности относится к длине диаметра приближенно как 22:7. Найдите длину
- 44. Верхушка головы - где 1,7м рост человека. Ноги прошли путь , где R радиус земного шара.
- 45. Обычно отвечают, что промежуток будет тоньше волоса. Если обтянуть земной шар по экватору проволокой и затем
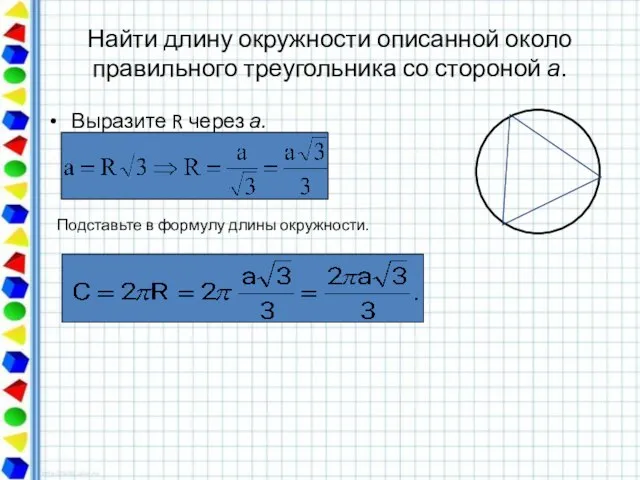
- 46. Найти длину окружности описанной около правильного треугольника со стороной а. Выразите R через а. Подставьте в
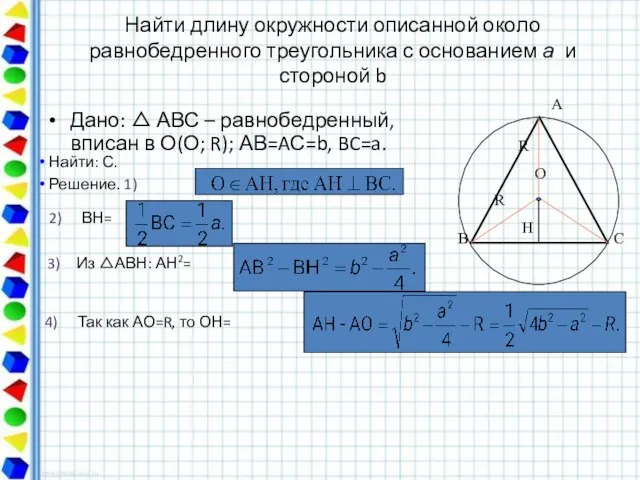
- 47. R O R H Дано: АВС – равнобедренный, вписан в О(О; R); АВ=AС=b, BC=a. Найти
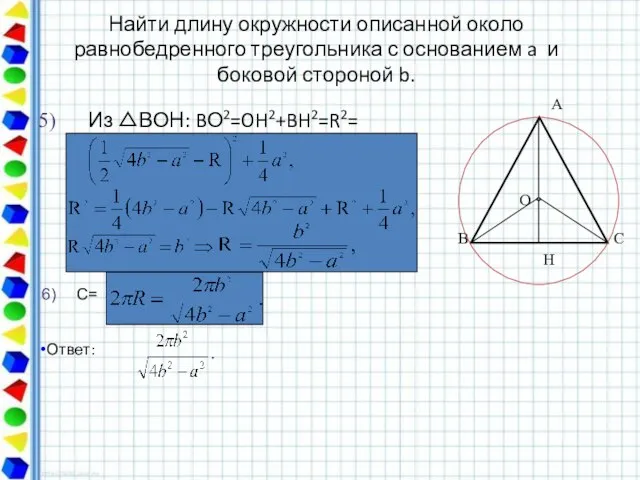
- 48. Найти длину окружности описанной около равнобедренного треугольника с основанием a и боковой стороной b. Из ВОН:
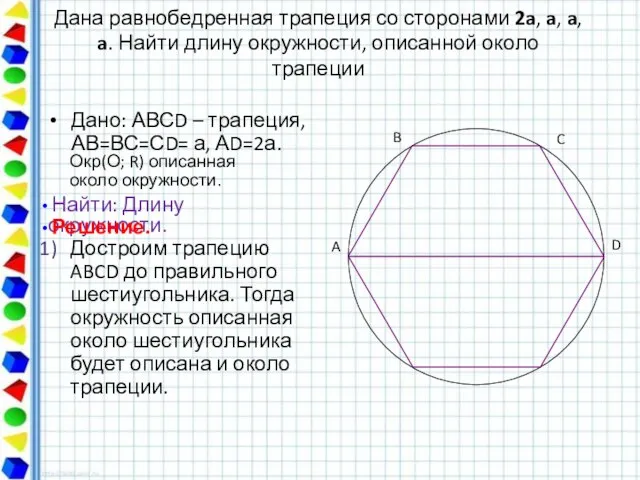
- 49. Дана равнобедренная трапеция со сторонами 2a, a, a, a. Найти длину окружности, описанной около трапеции Дано:
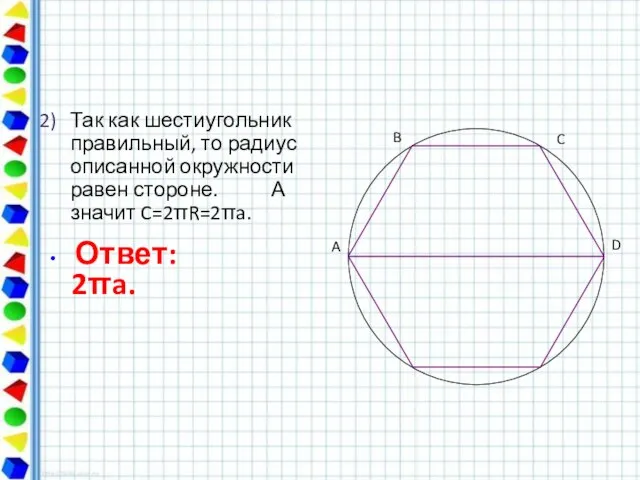
- 50. Так как шестиугольник правильный, то радиус описанной окружности равен стороне. А значит C=2R=2a. Ответ: 2a. A
- 51. Архимед в III в. до н.э. обосновал в своей небольшой работе "Измерение круга" три положения: всякий
- 52. В первой половине XV в. обсерватории Улугбека, возле Самарканда, астроном и математик ал-Каши вычислил "пи" с
- 53. Интересные факты Отношение длины основания Великой Пирамиды к ее высоте, разделенное пополам, дает знаменитое число "пи"
- 54. Интересные факты Лидером по тупым законам по праву может считаться Американский штат Индиана. Там на ряду
- 56. Скачать презентацию





































 Сферическая поверхность. Шар Геометрия 11 класс
Сферическая поверхность. Шар Геометрия 11 класс Площадь многоугольника 8 класс
Площадь многоугольника 8 класс Рисунок «Бегемотик» на координатной плоскости
Рисунок «Бегемотик» на координатной плоскости Введение в стереометрию
Введение в стереометрию Средняя линия треугольника 8 класс
Средняя линия треугольника 8 класс Круги Эйлера и их практическое применение
Круги Эйлера и их практическое применение Приготовьтесь к построению
Приготовьтесь к построению Гладунец Ирина Владимировна Учитель математики МБОУ гимназии №1 г.Лебедянь Липецкой области
Гладунец Ирина Владимировна Учитель математики МБОУ гимназии №1 г.Лебедянь Липецкой области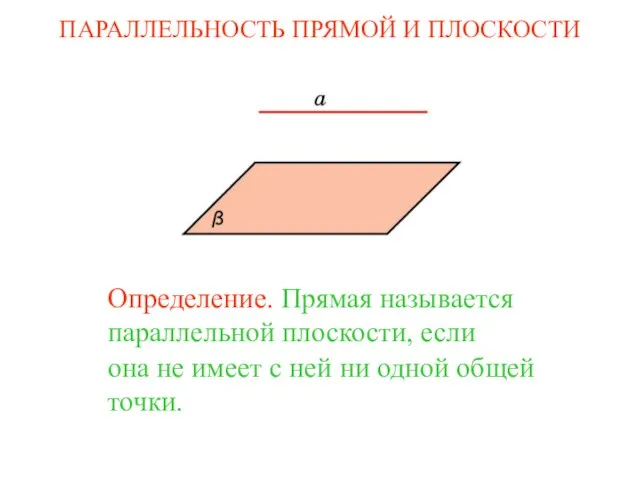 Параллельность прямой и плоскости
Параллельность прямой и плоскости Свойство точек биссектрисы угла.
Свойство точек биссектрисы угла. Вокруг храма с линейкой и циркулем
Вокруг храма с линейкой и циркулем Теорема о трех перпендикулярах в задачах 10 заочное обучение
Теорема о трех перпендикулярах в задачах 10 заочное обучение Виды углов. Измерение углов
Виды углов. Измерение углов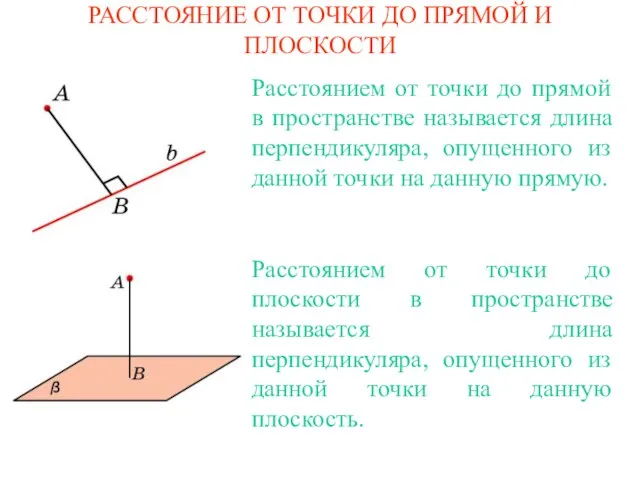 Расстояние от точки до прямой и плоскости
Расстояние от точки до прямой и плоскости Прямоугольник и его свойства
Прямоугольник и его свойства Пирамиды
Пирамиды Пифагоровы штаны во все стороны равны
Пифагоровы штаны во все стороны равны Координатный метод
Координатный метод Приращение функции и приращение аргумента
Приращение функции и приращение аргумента Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________
Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________ Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Решение прямоугольных треугольников
Решение прямоугольных треугольников Разные способы нахождения площади многоугольников
Разные способы нахождения площади многоугольников Первый признак равенства треугольников
Первый признак равенства треугольников Первый урок геометрии в 7 классе
Первый урок геометрии в 7 классе Смежные и вертикальные углы
Смежные и вертикальные углы вид разреза сечения
вид разреза сечения Секреты квадрата и кубика
Секреты квадрата и кубика