Содержание
- 2. Геометрические фигуры Геометрия – это наука о свойствах геометрических фигур. Слово «геометрия» греческое, в переводе на
- 3. Всякую геометрическую фигуру мы представляем себе составленной из точек
- 4. В школе изучается геометрия, называемая евклидовой, по имени Евклида, создавшего руководство по математике под названием «Начала».
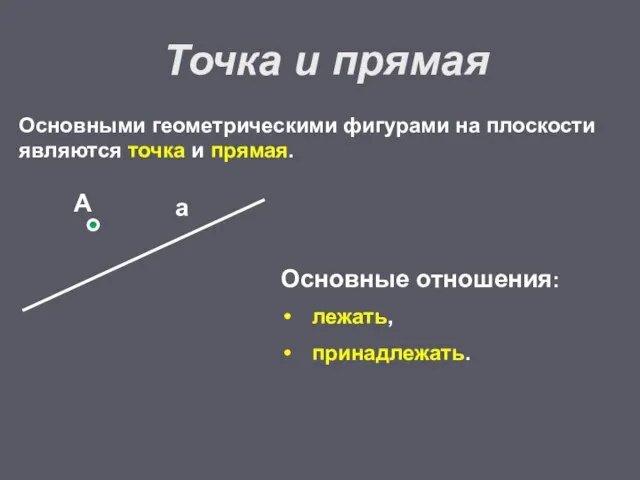
- 5. Основными геометрическими фигурами на плоскости являются точка и прямая. Точка и прямая Основные отношения: лежать, принадлежать.
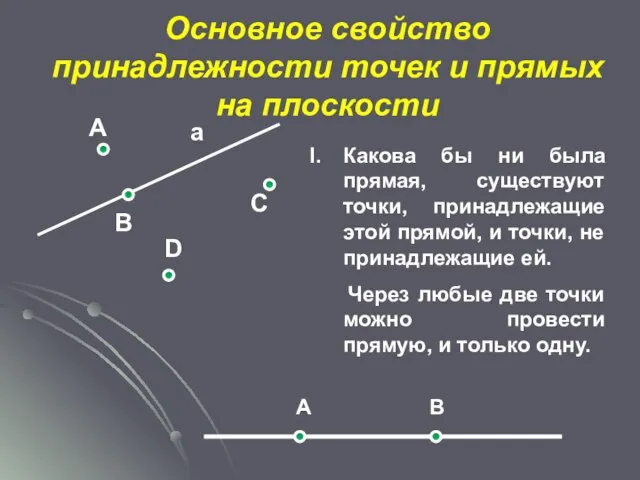
- 6. А а В С D Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и
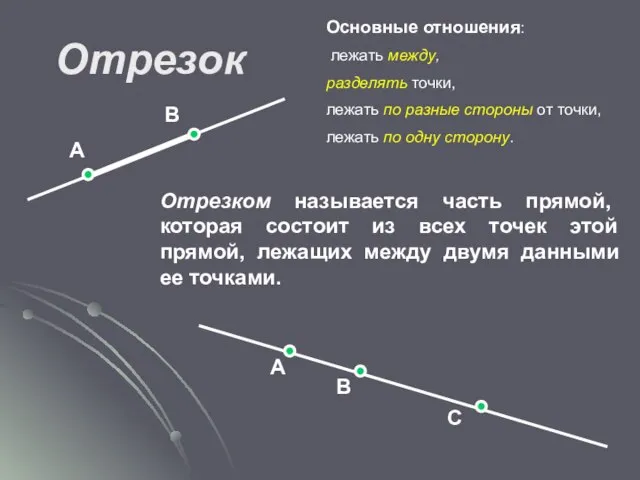
- 7. Отрезок Основные отношения: лежать между, разделять точки, лежать по разные стороны от точки, лежать по одну
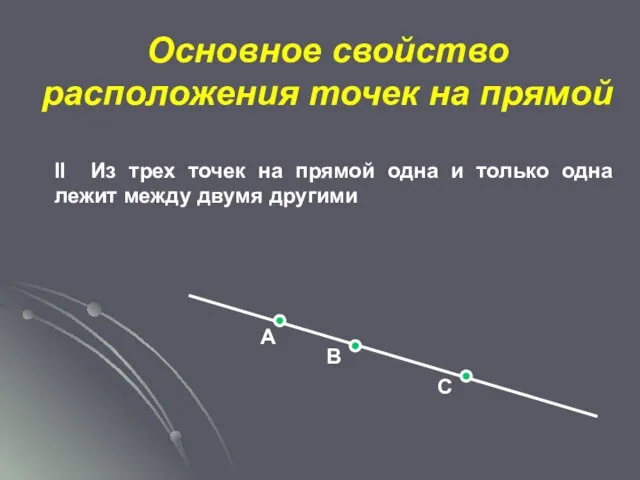
- 8. Основное свойство расположения точек на прямой А В С II Из трех точек на прямой одна
- 9. Основное свойство измерения отрезков Для измерения отрезков применяют различные измерительные инструменты III Каждый отрезок имеет определенную
- 10. Полуплоскости А В С D Основное свойство расположения точек относительно прямой на плоскости IV Прямая разбивает
- 11. Полупрямая А Х У Z Полупрямой или лучом называется часть прямой, которая состоит из всех точек
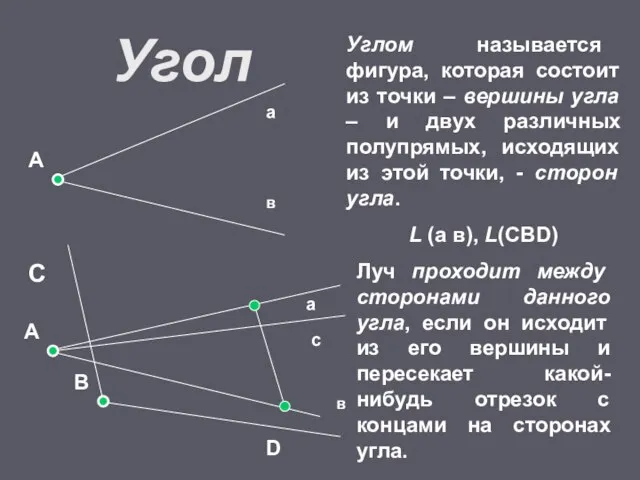
- 12. Угол В А а в С D Углом называется фигура, которая состоит из точки – вершины
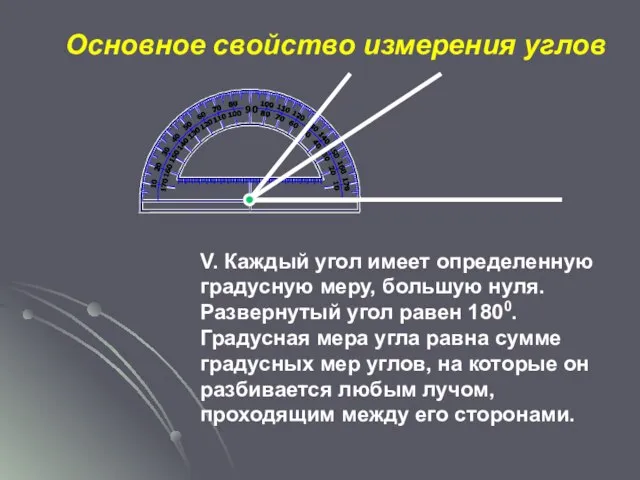
- 13. Основное свойство измерения углов V. Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен
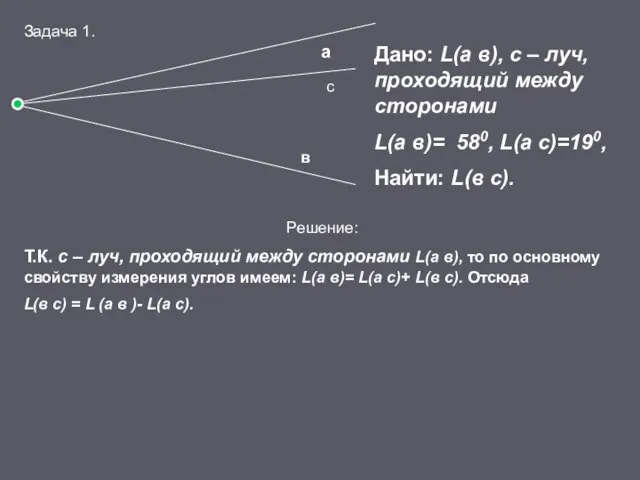
- 14. а в с Дано: L(а в), с – луч, проходящий между сторонами L(а в)= 580, L(а
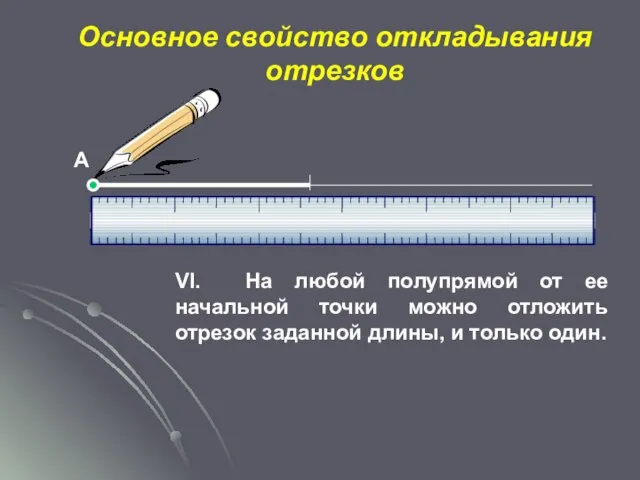
- 15. Основное свойство откладывания отрезков VI. На любой полупрямой от ее начальной точки можно отложить отрезок заданной
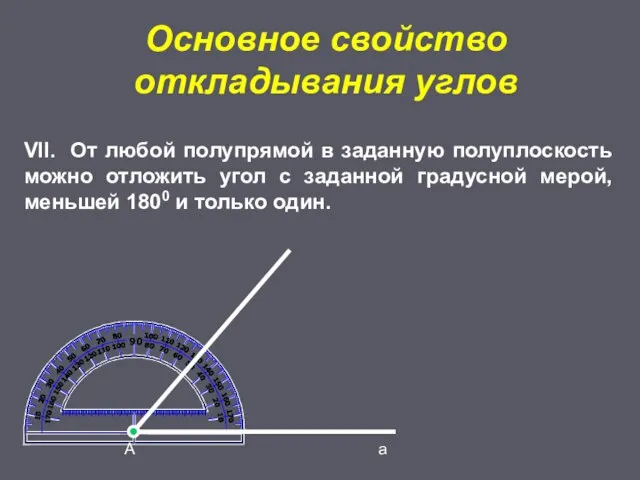
- 16. Основное свойство откладывания углов А а VII. От любой полупрямой в заданную полуплоскость можно отложить угол
- 17. Измерение углов на местности Измерение углов на местности проводится с помощью специальных приборов. Простейшим из них
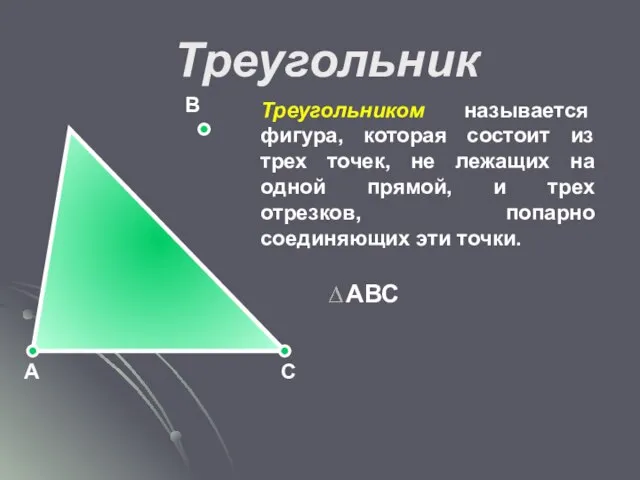
- 19. Треугольник Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех
- 20. А M В С N K
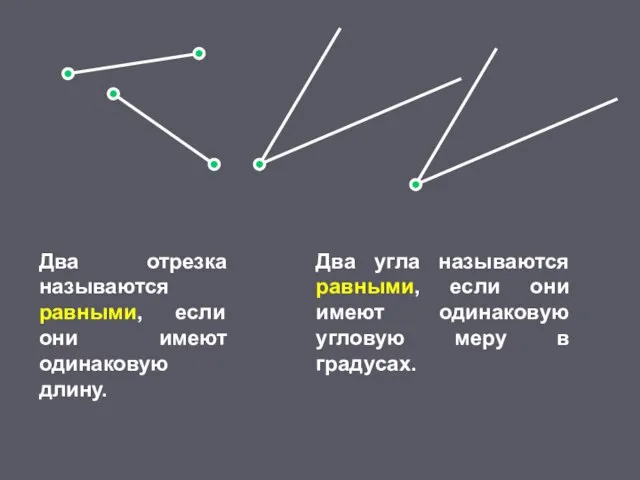
- 21. Два отрезка называются равными, если они имеют одинаковую длину. Два угла называются равными, если они имеют
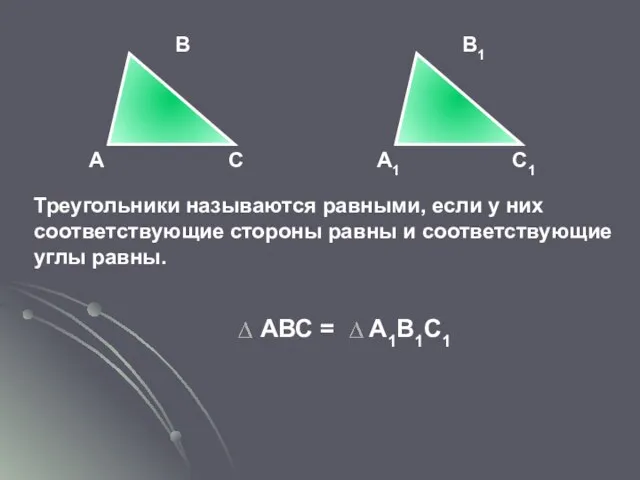
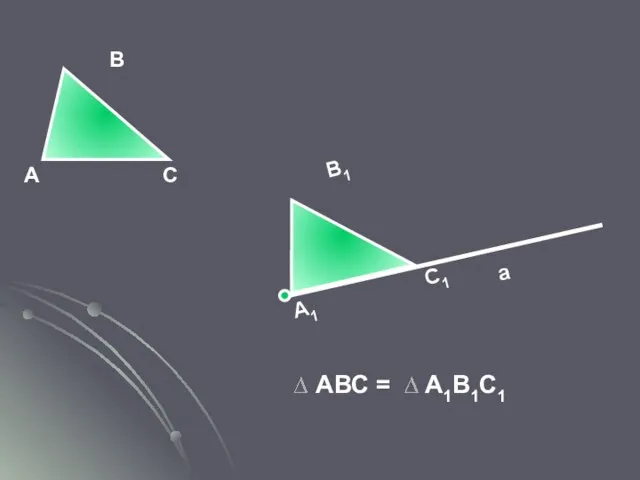
- 22. А С В А1 С1 В1 Треугольники называются равными, если у них соответствующие стороны равны и
- 23. Основное свойство существования треугольника равного данному VIII. Каков бы ни был треугольник, существует равный ему треугольник
- 24. А С В А1 С1 В1 АВС = А1В1С1 а
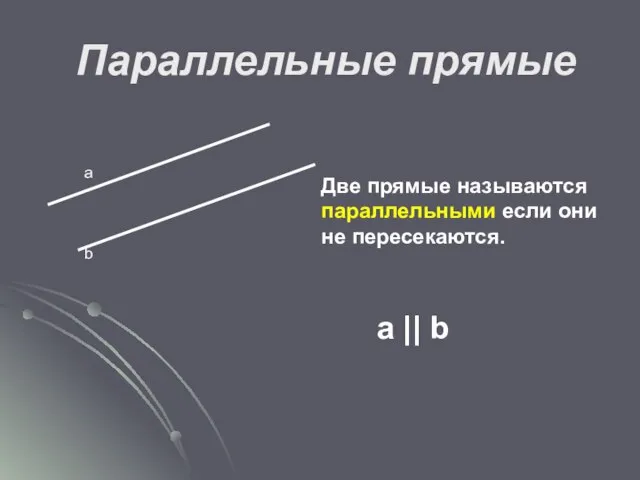
- 25. Параллельные прямые а b Две прямые называются параллельными если они не пересекаются. а || b
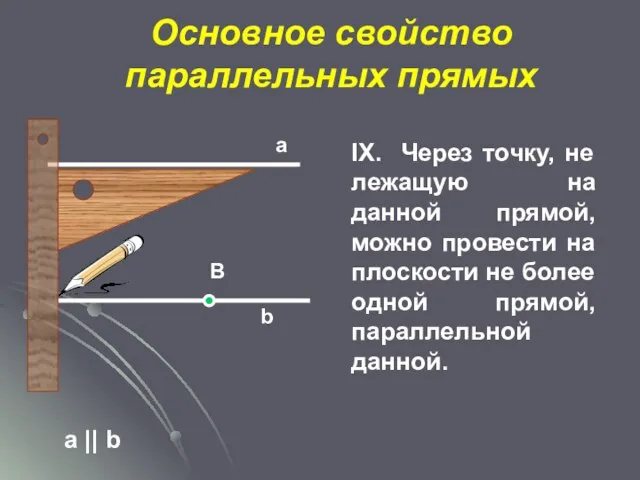
- 26. Основное свойство параллельных прямых а || b а В b IX. Через точку, не лежащую на
- 27. В развитии геометрии важную роль сыграла аксиома, которая в «Началах…» Евклида называлась пятым постулатом (аксиома параллельности
- 28. Лобачевский не получил противоречивых выводов. На основании этого им был сделан замечательный вывод: можно построить другую
- 29. Аксиомы. Теоремы и доказательства Утверждения, принимаемые без доказательств, называются аксиомами. Утверждение, истинность которого необходимо доказать, называется
- 31. Скачать презентацию













 Сумма углов треугольника 7 класс
Сумма углов треугольника 7 класс Тест по теме: «Площади многоугольников»
Тест по теме: «Площади многоугольников» Теорема Пифагора 7-9 класс
Теорема Пифагора 7-9 класс Трапеция
Трапеция Геометрические фигуры (Взаимное расположение на плоскости)
Геометрические фигуры (Взаимное расположение на плоскости) Трисекция угла
Трисекция угла Двугранные углы - презентация по Геометрии_
Двугранные углы - презентация по Геометрии_ Мир многогранников
Мир многогранников Применение параллелограмма
Применение параллелограмма Красота, гармония, симметрия
Красота, гармония, симметрия Площади плоских геометрических фигур
Площади плоских геометрических фигур Цилиндр и конус
Цилиндр и конус Решение прямоугольных треугольников
Решение прямоугольных треугольников Классификация геометрических объектов
Классификация геометрических объектов Почему квадрат?
Почему квадрат? Сечения многогранников плоскостью
Сечения многогранников плоскостью «Чтение графиков. ЕГЭ» ЮВАО
«Чтение графиков. ЕГЭ» ЮВАО Теоремы синусов и косинусов
Теоремы синусов и косинусов ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ Петрова Людмила Анатольевна, учитель математики, г.Санкт-Петербург, лицей № 1
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ Петрова Людмила Анатольевна, учитель математики, г.Санкт-Петербург, лицей № 1 Сложение, вычитание, умножение, деление натуральных чисел. Угол, треугольник, прямоугольник
Сложение, вычитание, умножение, деление натуральных чисел. Угол, треугольник, прямоугольник Что такое окружность? - презентация по Геометрии_
Что такое окружность? - презентация по Геометрии_ Длина окружности. Площадь круга
Длина окружности. Площадь круга Шар. Сфера
Шар. Сфера Параллельные прямые
Параллельные прямые Сфера
Сфера Параллельные прямые 6 класс
Параллельные прямые 6 класс Графы и их применение
Графы и их применение Взаимное положение прямых Начертательная геометрия 11 класс
Взаимное положение прямых Начертательная геометрия 11 класс