Содержание
- 2. Рассмотрим задачу линейного программирования в виде Назовем эту задачу исходной. Постановка двойственной задачи линейного программирования Тогда
- 3. Двойственная задача линейного программирования ставится следующим образом. 1. В исходной задаче в двойственной 2. Коэффициенты при
- 4. 4. Свободный коэффициент функции F равен свободному коэффициенту функции L. 5. Матрица коэффициентов ограничений двойственной задачи
- 5. Лемма (основное неравенство) Пусть и – допустимые наборы (то есть опорные планы) исходной и двойственной задач
- 6. Рассмотрим поскольку для любого Отсюда Теперь рассмотрим поскольку для любого Отсюда Сравниваем полученные неравенства и замечаем,
- 7. Теорема (о двойственных задачах) Пусть и – допустимые наборы исходной и двойственной задач соответственно. Равенство имеет
- 8. Доказательство. Если для допустимых наборов, то для любого допустимого набора из основного неравенства Следовательно, является решением
- 9. Замечание. Обратное ко второму утверждению неверно. Если область допустимых решений двойственной задачи пуста, то из этого
- 10. Установим соответствие между переменными. Соответствие между исходной и двойственной задачами линейного программирования
- 11. Лемма (о дополняющей нежесткости) Пусть и – решения исходной и двойственной задачи соответственно. Выполнены следующие соотношения.
- 12. Доказательство. Рассмотрим С другой стороны, Заметим, что так и – решения, то а, следовательно, Отсюда, Тогда
- 13. Но поскольку получаем Так как то для любого и для любого Отсюда и следует утверждение леммы.
- 14. Замечание. Из второй теоремы двойственности для рассматриваемых симплекс-таблиц следует, что переменные, соответствующие базисным переменным исходной задачи,
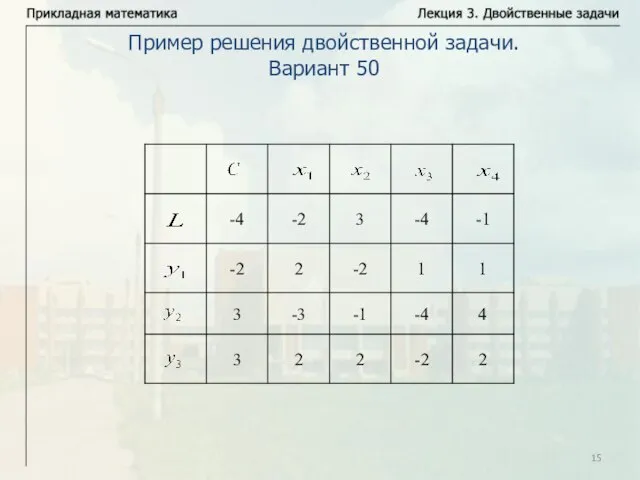
- 15. Пример решения двойственной задачи. Вариант 50
- 16. Задача, соответствующая этой симплекс-таблице имеет вид Ограничения можно записать в виде Пример решения двойственной задачи
- 17. Двойственная задача ставится следующим образом Пример решения двойственной задачи Дополнительные переменные двойственной задачи удовлетворяют неравенствам
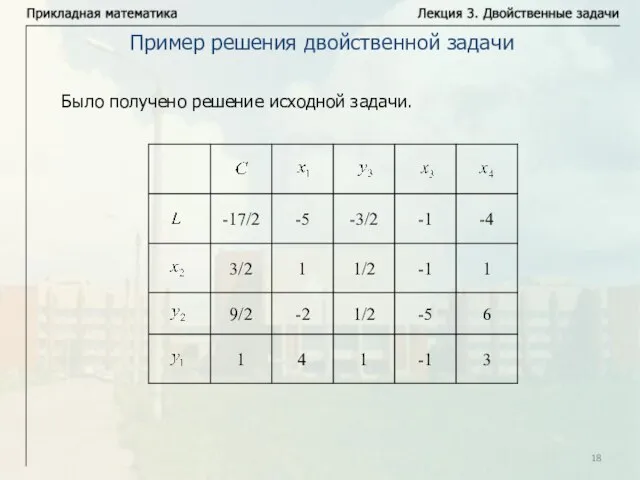
- 18. Было получено решение исходной задачи. Пример решения двойственной задачи
- 19. Из второй теоремы двойственности По лемме о дополняющей нежесткости следовательно, Это совпадает с полученными результатами. Пример
- 20. В двойственной задаче линейного программирования целевая функция … исследуется на минимум; исследуется на максимум; неотрицательна; равна
- 21. Задания для самоконтроля 2. Ограничения в двойственной задаче задаются при помощи знаков…
- 22. 3. Свободные коэффициенты целевых функций в прямой и двойственной задаче линейного программирования… положительны; равны; взаимно обратны;
- 23. Задания для самоконтроля 4. Матрица коэффициентов ограничений двойственной задачи по отношению к соответствующей матрице исходной задачи
- 25. Скачать презентацию




















 Теорема Пифагора
Теорема Пифагора Классы интегрируемых функций
Классы интегрируемых функций Интеллектуальная игра по математике для 8 класса
Интеллектуальная игра по математике для 8 класса Движение в геометрии
Движение в геометрии Математическая модель
Математическая модель Примеры. Карточки, счет +-10, 11, 12
Примеры. Карточки, счет +-10, 11, 12 Анализ уравнения на соответствие графику
Анализ уравнения на соответствие графику Масса предметов
Масса предметов Теория игр
Теория игр Методика изучения площади
Методика изучения площади Элементы комбинаторики. Перестановки
Элементы комбинаторики. Перестановки Линейная зависимость и линейная независимость системы векторов. Семинар 4
Линейная зависимость и линейная независимость системы векторов. Семинар 4 Осевая семетрия
Осевая семетрия Координатная плоскость. Ордината. Абсцисса
Координатная плоскость. Ордината. Абсцисса Алгоритм и письменное деление на двузначное число
Алгоритм и письменное деление на двузначное число Темір жолдың жылжымалы құрамын пайдалану, жөндеу және техникалық қызмет көрсету (түрлері бойынша)
Темір жолдың жылжымалы құрамын пайдалану, жөндеу және техникалық қызмет көрсету (түрлері бойынша)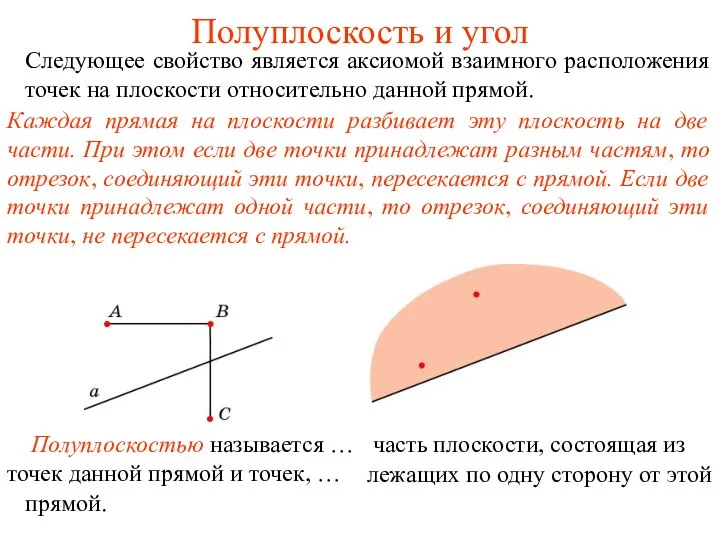 Полуплоскость и угол
Полуплоскость и угол Компланарны ли тройки векторов
Компланарны ли тройки векторов Четырехугольники
Четырехугольники Общее уравнение прямой и плоскости. Лекция1 (1)
Общее уравнение прямой и плоскости. Лекция1 (1) Математика интелектуальная разминка
Математика интелектуальная разминка Усеченый конус
Усеченый конус Кратчайшие расстояния
Кратчайшие расстояния Параллельные прямые 7 класс
Параллельные прямые 7 класс Таблица истинности
Таблица истинности Готфрид Лейбниц (1646 – 1716) – немецкий математик, физик, философ, юрист, языковед
Готфрид Лейбниц (1646 – 1716) – немецкий математик, физик, философ, юрист, языковед Таблицы данных с двумя переменными
Таблицы данных с двумя переменными Показательные уравнения и неравенства
Показательные уравнения и неравенства