Содержание
- 2. Понятие "фрактал". Понятия фрактал и фрактальная геометрия, появившиеся в конце 70-х, с середины 80-х прочно вошли
- 3. Понятие фрактала Фрактал — это бесконечно самоподобная геометрическая фигура, каждый фрагмент которой повторяется при уменьшении масштаба.
- 4. Проект "Фракталы - это наука или красота"
- 6. Проект "Фракталы - это наука или красота"
- 7. Разветвления трубочек трахей, листья на деревьях, вены в руке, река, бурлящая и изгибающаяся, рынок ценных бумаг
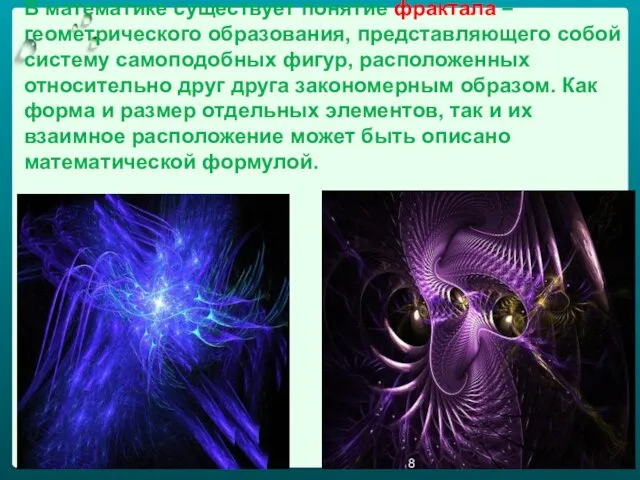
- 8. В математике существует понятие фрактала – геометрического образования, представляющего собой систему самоподобных фигур, расположенных относительно друг
- 9. Роль фракталов Роль фракталов в компьютерной графике сегодня достаточно велика. Они приходят на помощь, например, когда
- 10. Фрактал - геометрическая фигура, состоящая из частей, которые могут быть поделены на части, каждая из которых
- 11. Свойства фракталов Одним из основных свойств фракталов является самоподобие. В самом простом случае небольшая часть фрактала
- 12. ФРАКТАЛЫ – ЭТО ЯЗЫК ГЕОМЕТРИИ Фрактальная графика - это модель структуры и принципа любого сущего. ФРАКТАЛ
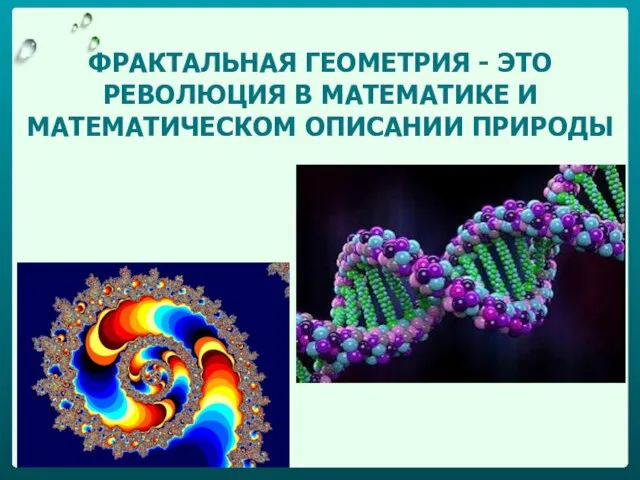
- 13. ФРАКТАЛЬНАЯ ГЕОМЕТРИЯ - ЭТО РЕВОЛЮЦИЯ В МАТЕМАТИКЕ И МАТЕМАТИЧЕСКОМ ОПИСАНИИ ПРИРОДЫ
- 14. ФРАКТАЛЫ В ПРИРОДЕ
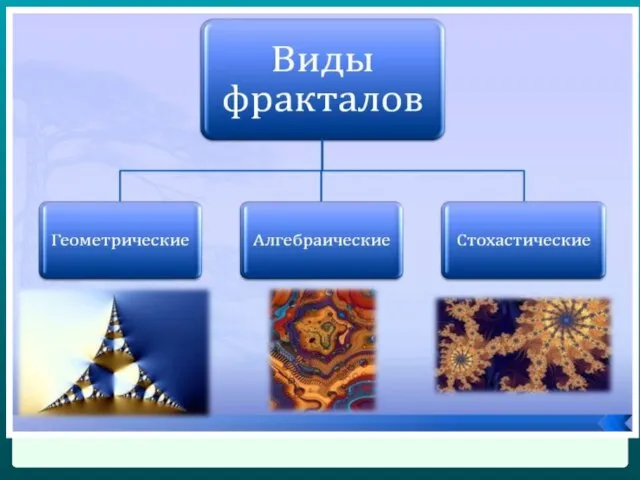
- 18. Это «функции - монстры», которых так называли за недифференцируемость в каждой точке. Геометрические фракталы являются также
- 19. Геометрические фракталы Именно с них и начиналась история фракталов. Этот тип фракталов получается путем простых геометрических
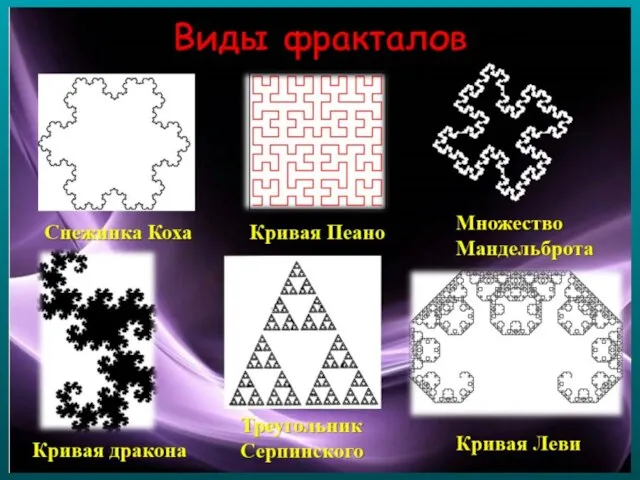
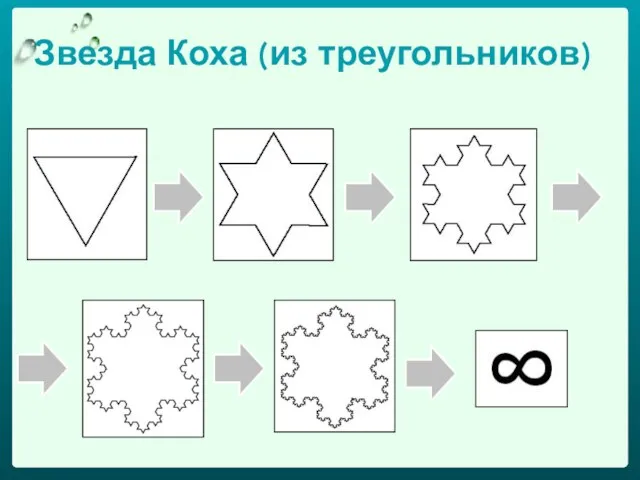
- 21. Из геометрических фракталов очень интересным и знаменитым является снежинка Коха. Строится она на основе равностороннего треугольника.
- 22. Звезда Коха (из треугольников)
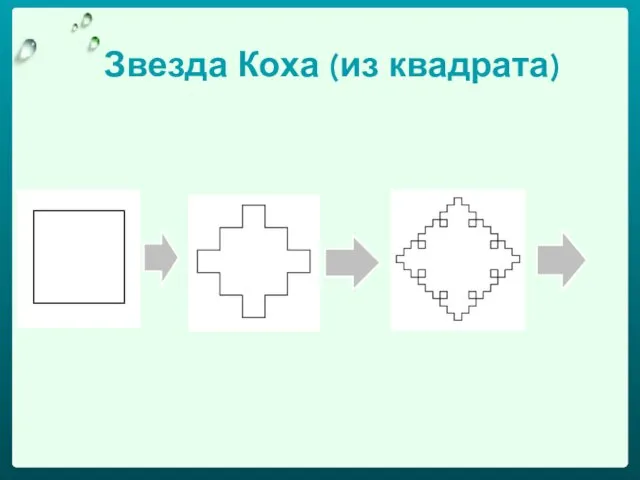
- 23. Звезда Коха (из квадрата)
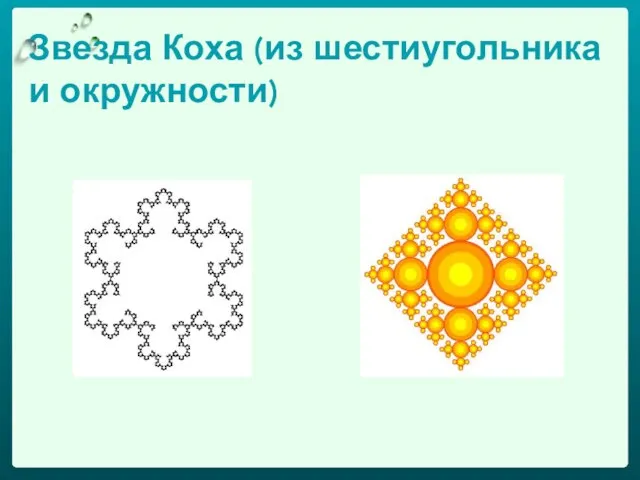
- 24. Звезда Коха (из шестиугольника и окружности)
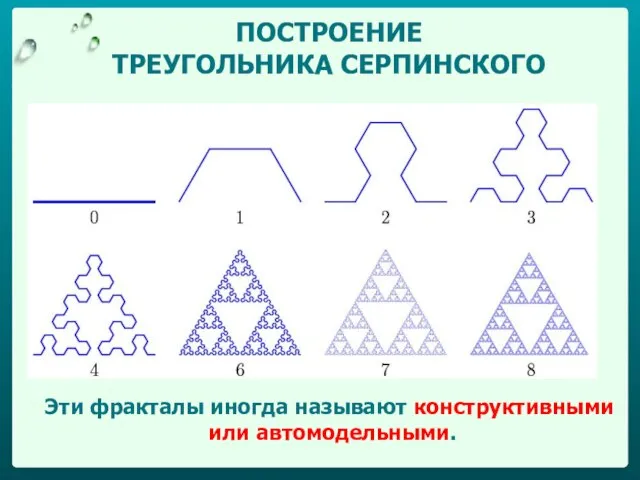
- 25. Треугольник Серпинского Для построения из центра равностороннего треугольника вырежем треугольник. Повторим эту же процедуру для трех
- 26. ПОСТРОЕНИЕ ТРЕУГОЛЬНИКА СЕРПИНСКОГО Эти фракталы иногда называют конструктивными или автомодельными.
- 27. Треугольник Серпинского
- 28. Проект "Фракталы - это наука или красота" Тетрикс (tetrix) – трехмерный аналог треугольника Серпинского
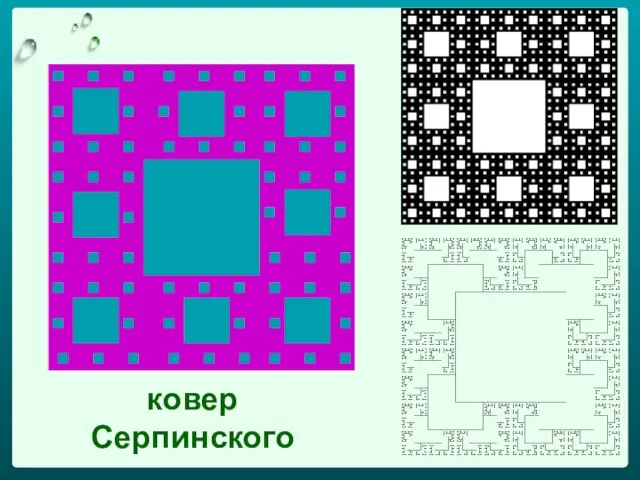
- 29. ковер Серпинского
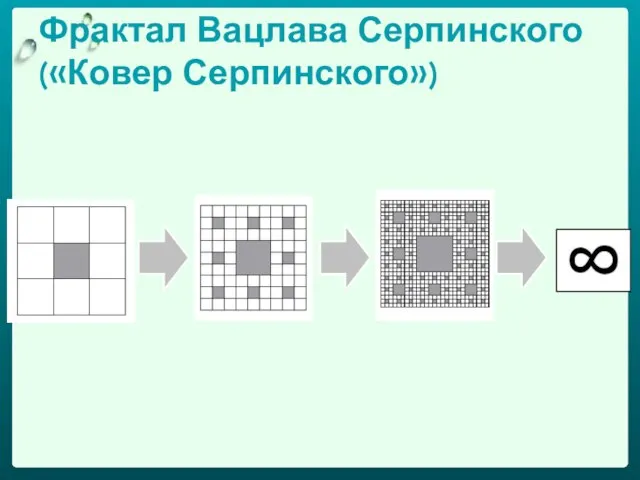
- 30. Фрактал Вацлава Серпинского («Ковер Серпинского»)
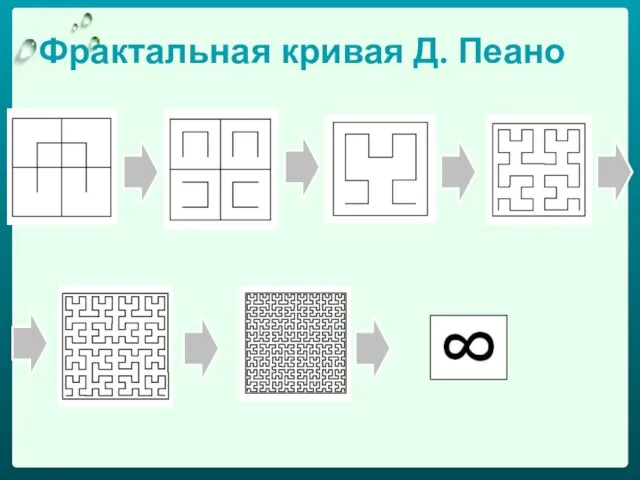
- 31. Фрактальная кривая Д. Пеано
- 32. “Кривая дракона” Э. Хейуэея
- 36. Еще примеры конструктивных фракталов
- 37. Алгебраические фракталы Вторая большая группа фракталов - алгебраические. Свое название они получили за то, что их
- 38. Это фракталы, которые можно построить, используя простые алгебраические формулы. Получают их с помощью нелинейных процессов в
- 39. Чтобы проиллюстрировать алгебраические фракталы обратимся к классике - множеству Мандельброта. Все множество Мандельброта в полной красе
- 40. Проект "Фракталы - это наука или красота"
- 41. Множество Жюлиа. Проект "Фракталы - это наука или красота"
- 42. Проект "Фракталы - это наука или красота"
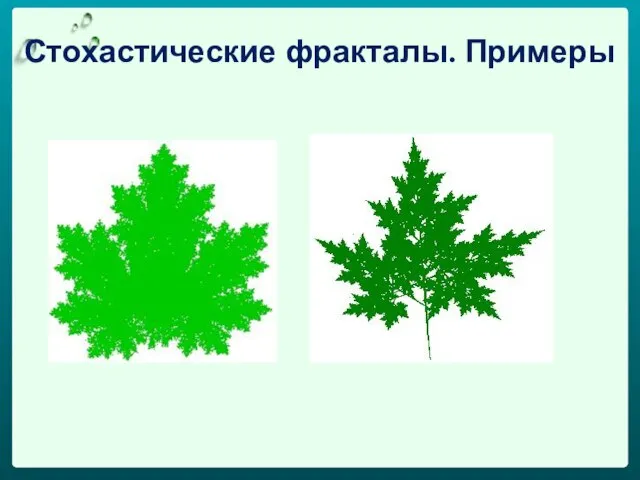
- 43. Это фракталы, при построении которых в итеративной системе случайным образом изменяются какие-либо параметры. Эти фракталы используются
- 45. Стохастические фракталы. Примеры
- 46. Стохастические фракталы. Примеры
- 47. Стохастические фракталы. Примеры
- 49. Свойства фракталов Самоподобие. Фракталы выражаются в виде математических уравнений. Характер большинства фрактальных алгоритмов рекурсивный. Теоретически глубина
- 51. ПРИМЕНЕНИЕ ФРАКТАЛОВ Физика и другие естественные науки Биология Литература Экономика. Анализ рынков Медицина Информатика Радиотехника Компьютерная
- 52. ПРИМЕНЕНИЕ ФРАКТАЛОВ В IT-ПРОФЕССИИ Радиотехника Создание фрактальных антенн Новый класс электрически малых антенн (ЭМА)
- 53. Применение фракталов Фракталы находят все большее и большее применение в науке. Основная причина этого заключается в
- 54. Компьютерные системы Наиболее полезным использованием фракталов в компьютерной науке является фрактальное сжатие данных. В основе этого
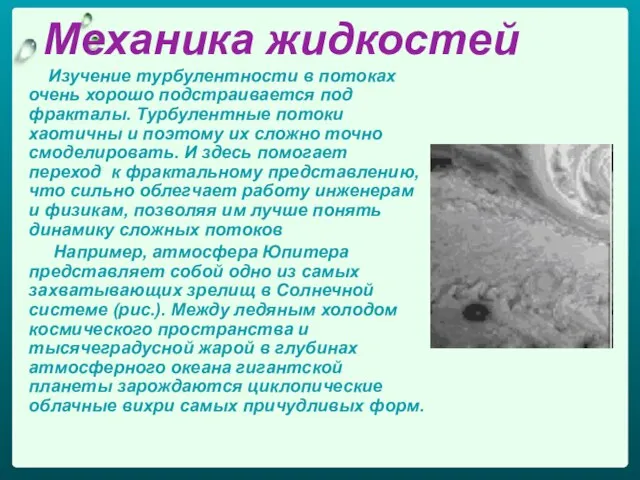
- 55. Механика жидкостей Изучение турбулентности в потоках очень хорошо подстраивается под фракталы. Турбулентные потоки хаотичны и поэтому
- 56. Телекоммуникации Для передачи данных на расстояния используются антенны, имеющие фрактальные формы, что сильно уменьшает их размеры
- 57. Физика поверхностей Фракталы используются для описания кривизны поверхностей. Неровная поверхность характеризуется комбинацией из двух разных фракталов.
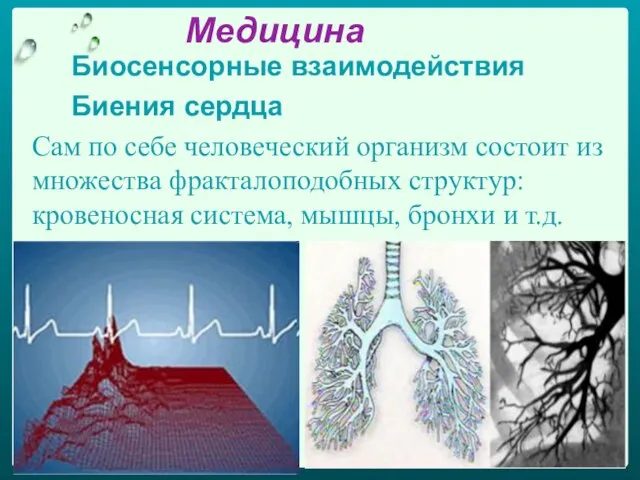
- 58. Медицина Биосенсорные взаимодействия Биения сердца Сам по себе человеческий организм состоит из множества фракталоподобных структур: кровеносная
- 59. Биология Моделирование хаотических процессов, в частности при описании моделей популяций В природе фрактальными свойствами обладают многие
- 60. Фрактальное искусство Еще одной захватывающей областью применения фракталов служит компьютерное искусство. Фракталы не только служат ученым,
- 61. В компьютерной графике фракталы применяются для построения изображений природных объектов, таких, как поверхности морей, деревья, кусты,
- 63. Скачать презентацию














































 Возведение в степень. Диктант
Возведение в степень. Диктант Вероятность в карточных играх
Вероятность в карточных играх Считаем со смешариками. Тренажер Сложенеие и вычитание в пределах 10.Технологический прием Анимированная сорбонка
Считаем со смешариками. Тренажер Сложенеие и вычитание в пределах 10.Технологический прием Анимированная сорбонка Целые числа. Обзор и контроль
Целые числа. Обзор и контроль Площадь многоугольника. Свойства площадей
Площадь многоугольника. Свойства площадей Дифференциальные уравнения. Лекция 3
Дифференциальные уравнения. Лекция 3 Практическая работа на целочисленное деление
Практическая работа на целочисленное деление Синус и тангенс
Синус и тангенс Методы решения логарифмических уравнений
Методы решения логарифмических уравнений Ортогональное проектирование. Перпендикуляр и наклонная. Угол между прямой и плоскостью. (Практическая работа)
Ортогональное проектирование. Перпендикуляр и наклонная. Угол между прямой и плоскостью. (Практическая работа) Курс по математике ОГЭ 2021
Курс по математике ОГЭ 2021 Пропорция – верное равенство двух отношений
Пропорция – верное равенство двух отношений Презентация на тему Действия с целыми числами
Презентация на тему Действия с целыми числами  Функции. Устная работа
Функции. Устная работа Показательные неравенства
Показательные неравенства Тетраэдр
Тетраэдр Решение задач на построение методом подобных треугольников
Решение задач на построение методом подобных треугольников розвязування трикутників
розвязування трикутників Призмы и антипризмы
Призмы и антипризмы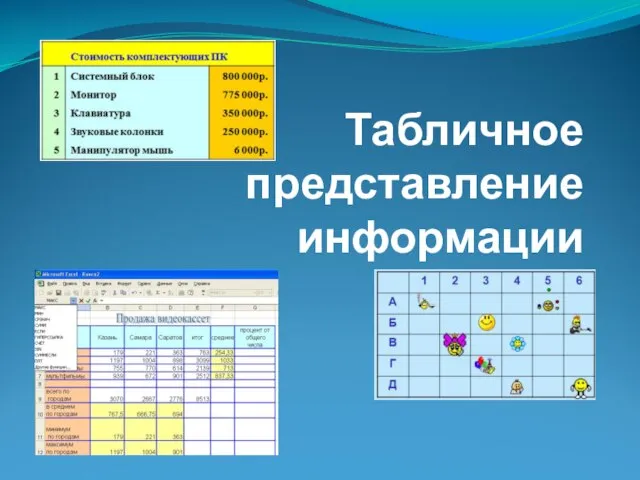 Табличное представление информации
Табличное представление информации Линейная алгебра. (Матрицы, определители)
Линейная алгебра. (Матрицы, определители) Дифференциальные уравнения и их применение в медицине
Дифференциальные уравнения и их применение в медицине Простейшие тригонометрические уравнения
Простейшие тригонометрические уравнения Как можно сравнивать размеры больших и малых тел
Как можно сравнивать размеры больших и малых тел Справочный материал. 9 класс
Справочный материал. 9 класс Арифметические действия в двоичной системе счисления
Арифметические действия в двоичной системе счисления Избранные вопросы и задачи планиметрии. Пособие для факультативных занятий
Избранные вопросы и задачи планиметрии. Пособие для факультативных занятий Геометричний метод розв’язування задач лінійного програмування. Методи оптимізації. Лекція №2
Геометричний метод розв’язування задач лінійного програмування. Методи оптимізації. Лекція №2