Координаты и векторы

Прямоугольная система координат в пространстве
Если через точку пространства проведены три попарно перпендикулярные прямые, на каждом из них выбрано направление(оно обозначается стрелкой) и выбрана единица измерения отрезков, то говорят, что задана прямоугольная (декартова) система координат в пространстве.

Прямые с выбранными на них направлениями называются осями координат, а их общая точка – началом координат. Обозначаются Oх, Oy, Oz.
Плоскости, проходящие соответственно через оси координат Ох и Оy, Oу и Оz, Oz и Ox, называются координатными плоскостями и обозначаются Oxy, Oхz, Ozy.
Точка О разделяет каждую из осей координат на два луча. Луч, направление которого совпадает с направлением оси, называется положительной полуосью, а другой луч – отрицательной полуосью.

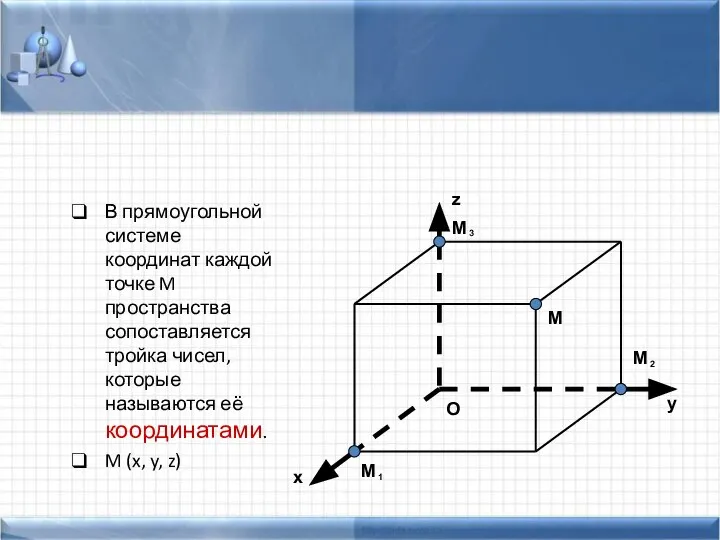
В прямоугольной системе координат каждой точке M пространства сопоставляется тройка чисел, которые называются её координатами.
M (x, y, z)
y
z
x
M
1
M
2
M
3
M
O

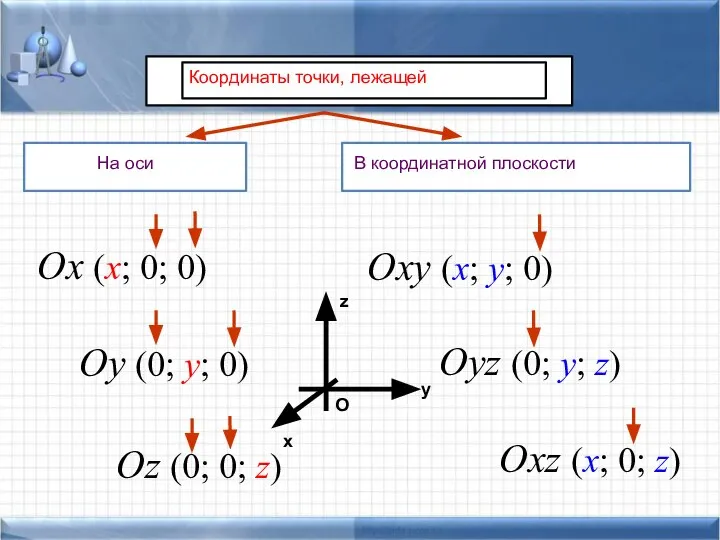
В координатной плоскости
Oxy (x; y; 0)
Oyz (0; y; z)
Oxz (x; 0; z)
Ox (x; 0; 0)
Oy (0; y; 0)
Oz (0; 0; z)
На оси

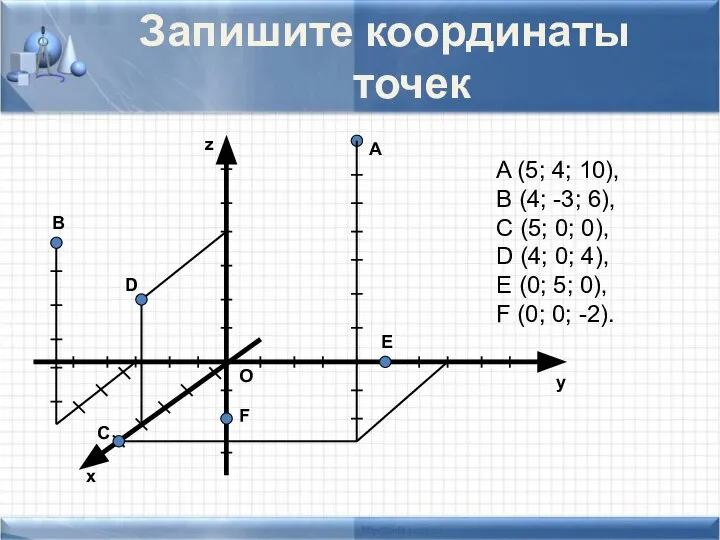
Запишите координаты точек
A (5; 4; 10),
B (4; -3; 6),
C (5; 0; 0),
D (4; 0; 4),
E (0; 5; 0),
F (0; 0; -2).

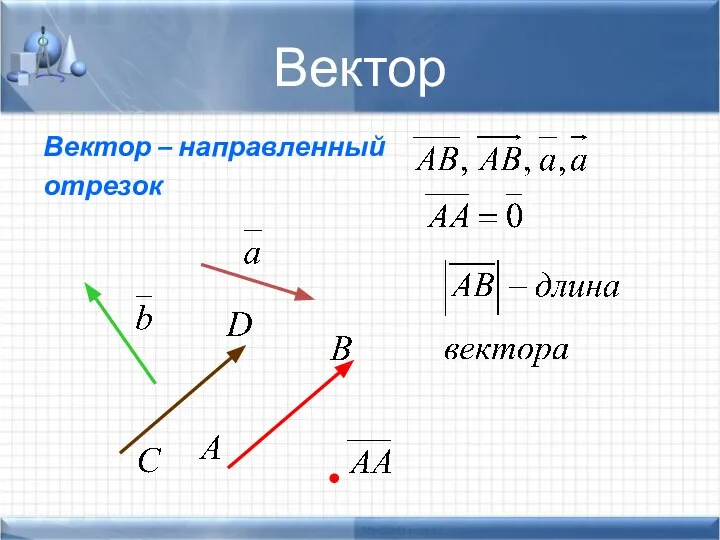
Вектор
Вектор – направленный
отрезок

Координаты вектора
Координаты вектора равны разности координат его конца и начала
Координаты вектора, началом которого является начало координат (радиус-вектора), равны координатам его конца.

Задача: Найдите координаты вектора АВ, если:

Абсолютная величина вектора
Абсолютная величина вектора
( модуль вектора, длина вектора) равна корню квадратному из
суммы квадратов его координат

Расстояние между точками
Расстояния между точка M (x ; y ; z ) и
M (x ; y ; z ) вычисляется по формуле
d = √(x – x )² + (y – y )² + (z – z )²
1
2
2
2
2
1
1
1
2 1 2 1 2 1

Задача: Найдите абсолютную величину вектора:

Правила нахождения суммы, разности и произведения на данное число.
Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.

Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.

Каждая координата произведения вектора на число равна произведение соответствующей координаты вектора на это число.
ka {kx; ky; kz}
a {x; y; z}