Содержание
- 2. «Множество» - это соединение в некое целое M определенных и хорошо различимых предметов m нашего созерцания
- 3. Приказ командира: брить тех и только тех, кто не бреется сам. А = {те и только
- 4. Способ Кантора: «Наивная теория множеств» Идея: разрешается работать со множествами, которые «встречаются в природе», а также
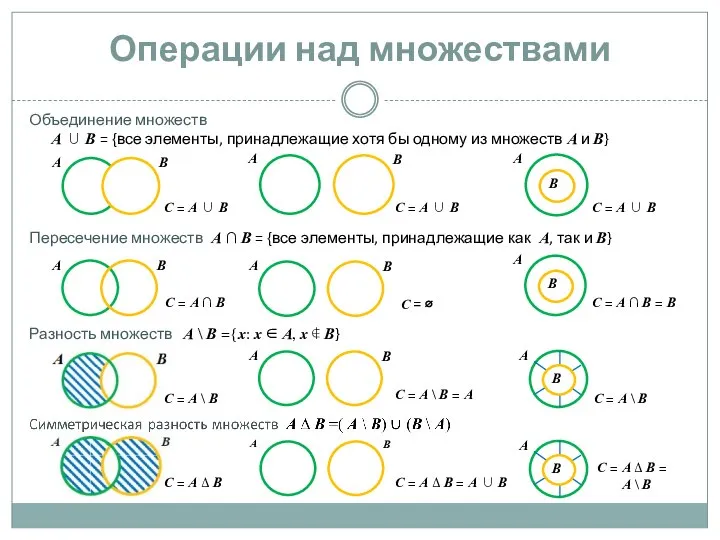
- 5. Операции над множествами Объединение множеств А ∪ В = {все элементы, принадлежащие хотя бы одному из
- 6. Основные тождества теории множеств Коммутативность объединения и пересечения А ∪ В = В ∪ А; А
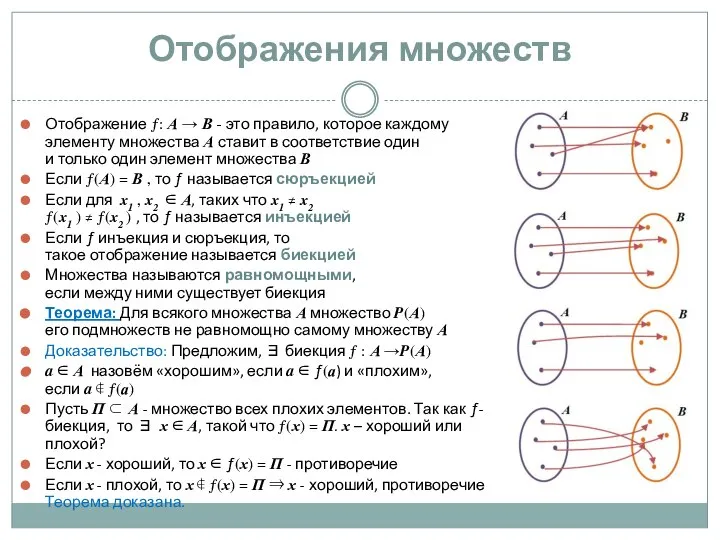
- 7. Отображения множеств Отображение ƒ: А → В - это правило, которое каждому элементу множества А ставит
- 8. Парадоксы с бесконечностью Дед Мороз пришел на Новый год к детям с мешком, в котором бесконечно
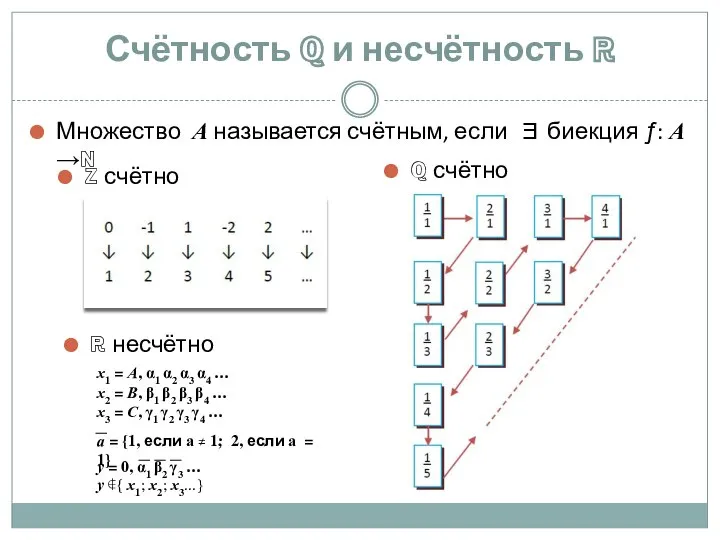
- 9. Счётность ℚ и несчётность ℝ Множество А называется счётным, если ∃ биекция ƒ: А →ℕ
- 11. Скачать презентацию





 Презентация на тему Натуральные числа (5 класс)
Презентация на тему Натуральные числа (5 класс) 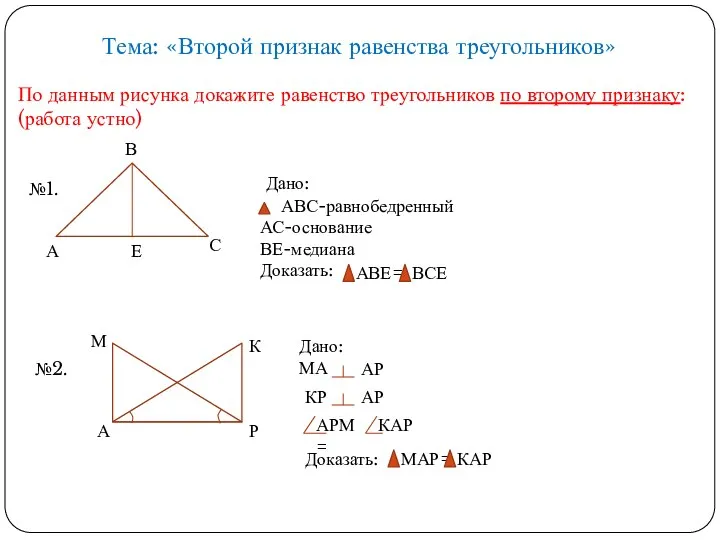 Равенство треугольников по второму признаку
Равенство треугольников по второму признаку Методы фильтрации контуров изображений
Методы фильтрации контуров изображений Неравенства. Обобщающий урок. Подготовка к ЕГЭ
Неравенства. Обобщающий урок. Подготовка к ЕГЭ Произведение вектора на число
Произведение вектора на число Лекция_03
Лекция_03 Геометрические иллюзии. Отрезок. Сравнение отрезков. Параллельные прямые
Геометрические иллюзии. Отрезок. Сравнение отрезков. Параллельные прямые Логарифм и его свойства
Логарифм и его свойства Основные теоремы теории вероятностей. Лекция 3
Основные теоремы теории вероятностей. Лекция 3 Сравнение чисел
Сравнение чисел 04.17.21.00[1]
04.17.21.00[1] Правило нахождения первообразной
Правило нахождения первообразной Разметка прямоугольника по угольнику
Разметка прямоугольника по угольнику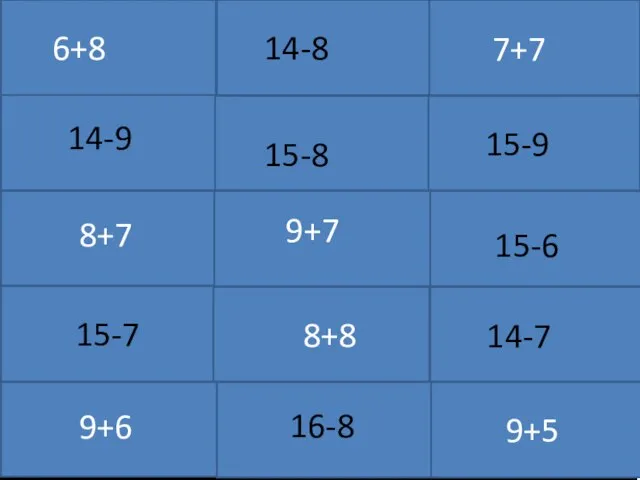 Примеры карточек. Счет +-10 11 12 13 14 15 16
Примеры карточек. Счет +-10 11 12 13 14 15 16 Четырёхугольники (повторение материала)
Четырёхугольники (повторение материала) Рациональные дроби. 8 класс
Рациональные дроби. 8 класс Геометрические построения
Геометрические построения Урок–путешествие в страну Дроби
Урок–путешествие в страну Дроби Сложение и вычитание числа 2
Сложение и вычитание числа 2 Станция Решай-ка. Математический экспресс
Станция Решай-ка. Математический экспресс Презентация на тему РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
Презентация на тему РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ  Разложим по полочкам задачи на смеси. Интегрированный урок по математике и химии
Разложим по полочкам задачи на смеси. Интегрированный урок по математике и химии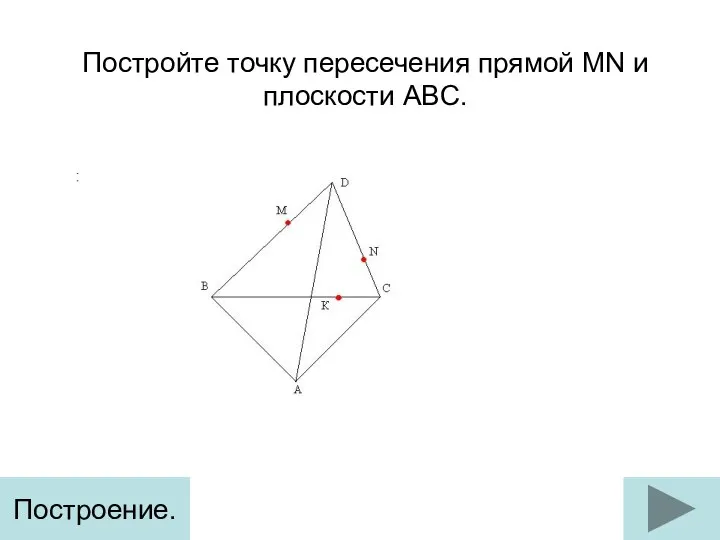 Точка пересечения прямой MN и плоскости ABC. Построение (задание 1)
Точка пересечения прямой MN и плоскости ABC. Построение (задание 1) Математический КВН. 6 класс
Математический КВН. 6 класс Подготовка к СР по теме Способ сложения при решений систем уравнений
Подготовка к СР по теме Способ сложения при решений систем уравнений Единицы времени
Единицы времени Решение задания В8. Основные типы заданий
Решение задания В8. Основные типы заданий Математика в экскурсиях
Математика в экскурсиях