Содержание
- 2. Производная Производная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной
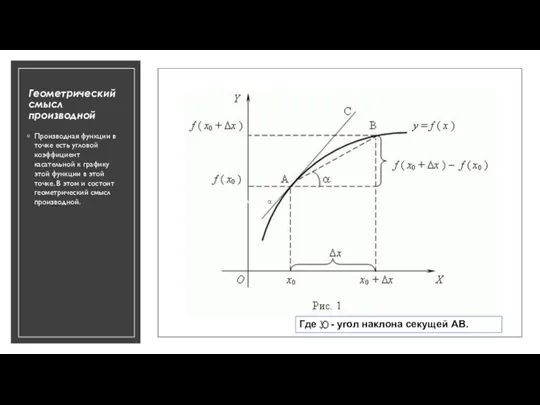
- 3. Геометрический смысл производной Производная функции в точке есть угловой коэффициент касательной к графику этой функции в
- 4. Механический смысл производной. Механический смысл производной состоит в том, что производная пути по времени равна мгновенной
- 6. Скачать презентацию


 Комбинаторика. Перебор вариантов. Решение задач
Комбинаторика. Перебор вариантов. Решение задач Полимино
Полимино Признаки равенства треугольников
Признаки равенства треугольников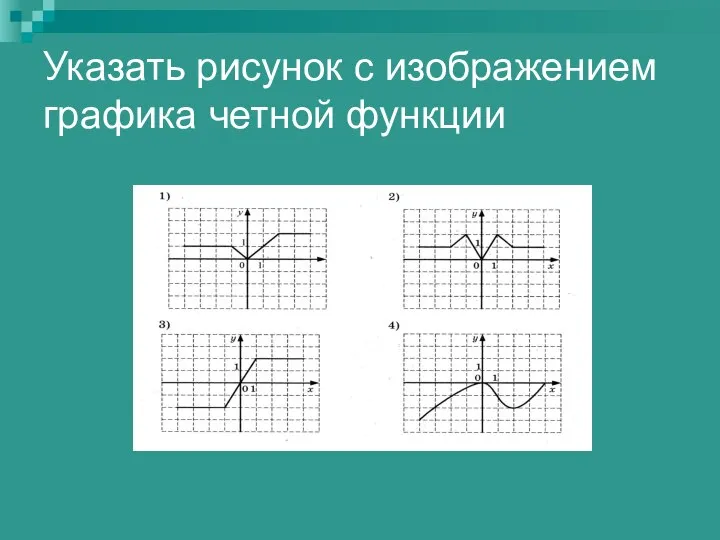 Указать рисунок с изображением графика четной функции
Указать рисунок с изображением графика четной функции Сантиметр Цель. В ходе практической работы и наблюдений познакомить учащихся 1 класса с единицей измерения длины – сантиметром.
Сантиметр Цель. В ходе практической работы и наблюдений познакомить учащихся 1 класса с единицей измерения длины – сантиметром. Уравнением с двумя переменными
Уравнением с двумя переменными Функція однієї змінної. Неперервність функції однієї змінної
Функція однієї змінної. Неперервність функції однієї змінної Свойства функции
Свойства функции Свойства случайных погрешностей
Свойства случайных погрешностей Морское путешествие
Морское путешествие Основные законы распределения непрерывных случайных величин
Основные законы распределения непрерывных случайных величин Задачи о наполнении сосуда
Задачи о наполнении сосуда Решение примеров и задач с числами в пределах 10
Решение примеров и задач с числами в пределах 10 Пропорция – верное равенство двух отношений
Пропорция – верное равенство двух отношений Решение уравнения методом последовательных приближений
Решение уравнения методом последовательных приближений Умножение и деление смешанных дробей
Умножение и деление смешанных дробей Симметрия. Виды симметрии
Симметрия. Виды симметрии Презентация на тему Декартовы координаты (8 класс)
Презентация на тему Декартовы координаты (8 класс)  Производная и ее применение
Производная и ее применение Вписанная и описанная окружности
Вписанная и описанная окружности Показательная функция, ее свойства и график
Показательная функция, ее свойства и график Задачи на построение угла
Задачи на построение угла Символика. Взаимное расположение точек и прямой
Символика. Взаимное расположение точек и прямой Теорема Пифагора
Теорема Пифагора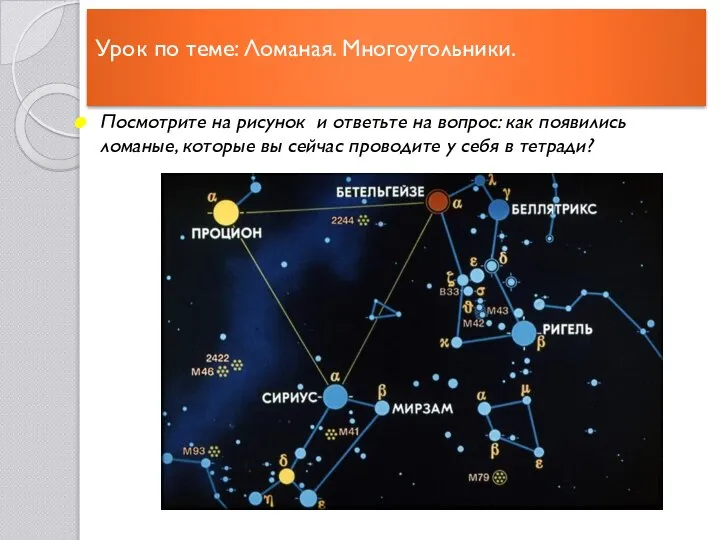 Ломаная. Многоугольники
Ломаная. Многоугольники 2
2 Свойства функции. Для повторения
Свойства функции. Для повторения Соотношения между сторонами и углами прямоугольного треугольника
Соотношения между сторонами и углами прямоугольного треугольника