Содержание
- 2. Дифференциальным уравнением (ДУ) называется уравнение, содержащее производные от искомой функции или её дифференциалы. или
- 3. Примеры ДУ:
- 4. Наивысший порядок производной, входящей в уравнение, называется порядком ДУ. Решением ДУ называется такая функция, подстановка которой
- 5. Пример: Показать, что данная функция является решением ДУ Т.о. функции вида являются решениями данного ДУ при
- 6. Дифференциальные уравнения I порядка
- 7. Общим решением ДУ I порядка называется функция , которая зависит от одного произвольного постоянного С. или
- 8. Частным решением ДУ I порядка называется любая функция полученная из общего решения при конкретном значении постоянной
- 9. Пример: ДУ: -общее решение частные решения
- 10. Геометрически: Общее решение ДУ есть семейство интегральных кривых на плоскости Оху; Частное решение ДУ -одна кривая
- 11. Задача отыскания конкретного частного решения данного ДУ по начальным данным называется задачей Коши (Cauchy). или Условие,
- 12. Пример: Решить задачу Коши: -общее решение Подставим в общее решение начальные условия: -частное решение х у
- 13. 1. ДУ I порядка с разделёнными переменными Если каждая часть ДУ представляет собой произведение некоторого выражения,
- 14. Пример: Решить ДУ С общее решение: или Геометрически: получили семейство концентрических окружностей с центром в начале
- 15. 2. ДУ I порядка с разделяющимися переменными Уравнения, в которых переменные разделяются, называются ДУ с разделяющимися
- 16. Пример: Найти общее и частное решение ДУ ⇒
- 17. Итак, общее решение ДУ: 2) Найдём частное решение ДУ, если Подставим эти начальные условия в общее
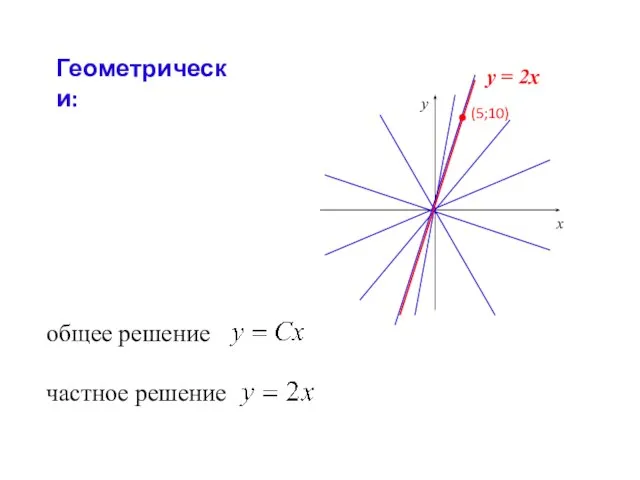
- 18. Геометрически: х у общее решение частное решение у = 2х (5;10)
- 19. Пример: Решить задачу Коши
- 21. Скачать презентацию

















 Учение о десятичных дробях
Учение о десятичных дробях Физический и механический смысл производных. Использование производной в физике, механике
Физический и механический смысл производных. Использование производной в физике, механике Устная работа. Разложите на множители
Устная работа. Разложите на множители Факторный анализ торговых алгоритмов
Факторный анализ торговых алгоритмов Умножение натуральных чисел. Графический диктант. 5 класс
Умножение натуральных чисел. Графический диктант. 5 класс Способы решения квадратных уравнений
Способы решения квадратных уравнений Вероятность случайного события. Математика
Вероятность случайного события. Математика Повторение курса геометрии. 7 класс
Повторение курса геометрии. 7 класс Графический диктант: Формулы
Графический диктант: Формулы Нестандартный урок математики. Проведен учителем I категории Крутько В.И.
Нестандартный урок математики. Проведен учителем I категории Крутько В.И. Плоскость. Лекция 8
Плоскость. Лекция 8 Задача с экологическим содержанием
Задача с экологическим содержанием Реши самостоятельно
Реши самостоятельно Розв'язання задач
Розв'язання задач Арифметическая прогрессия в истории
Арифметическая прогрессия в истории Свойства степени
Свойства степени График функции. Тест, 1-6 варианты
График функции. Тест, 1-6 варианты Матрицы. Прямоугольная таблица
Матрицы. Прямоугольная таблица Координатная плоскость. Задания для интерактивной доски
Координатная плоскость. Задания для интерактивной доски Естественный отбор и его математические характеристики
Естественный отбор и его математические характеристики Периметр, площадь, объём
Периметр, площадь, объём мощность множеств Леонгардт
мощность множеств Леонгардт Тригонометрические уравнения. Методы решения тригонометрических уравнений
Тригонометрические уравнения. Методы решения тригонометрических уравнений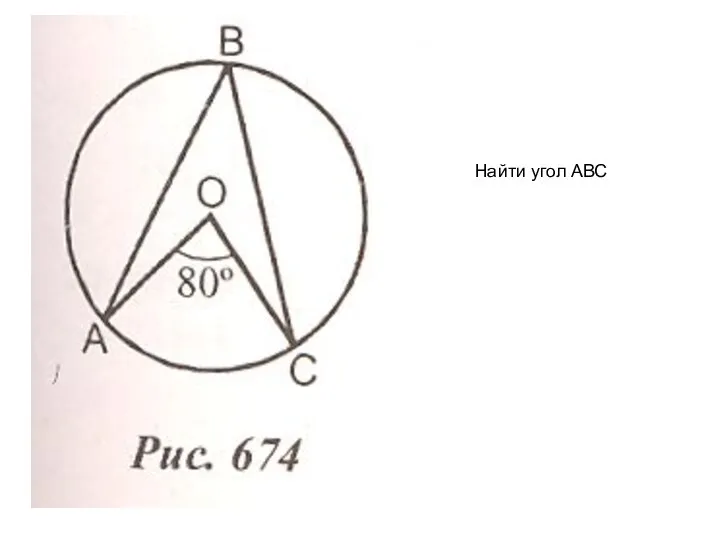 Найти угол АВС
Найти угол АВС Интеграл Лебега по измеримому в смысле Лебега множеству
Интеграл Лебега по измеримому в смысле Лебега множеству Приближенные значения чисел. Округление
Приближенные значения чисел. Округление В стране математики
В стране математики Задачи в координатах
Задачи в координатах