Решение задач на проценты, растворы и сплавы

Повторяем
Какие методы решения систем уравнений мы знаем?
Как подписываем столбцы, когда решаем задачу на движение?
Как подписываем столбцы, когда решаем задачу на стоимость?
Повторите русско-математический словарь ( презентация 24.04)
Повторите план решения задачи.

Особенности решения задач на проценты
В задачах на проценты удобно записывать проценты в виде частей (1% - это 0,01 часть чего-то, т.е. чтобы перевести проценты в части надо проценты разделить на 100), в задачах на сплавы и растворы также записываем концентрацию.
Чтобы найти часть от числа, надо умножить число на часть.
В таблицах для задач на растворы или сплавы столбцы подписываются стандартно: масса раствора (сплава), концентрация, масса вещества.

Задача на проценты
Двое рабочих должны были изготовить вместе 200 деталей. За первый день работы первый рабочий изготовил 60% количества деталей своего задания, а второй 80%. Сколько деталей должен изготовить каждый рабочий, если известно, что за первый день работы первый рабочий изготовил на 8 деталей больше, чем второй?
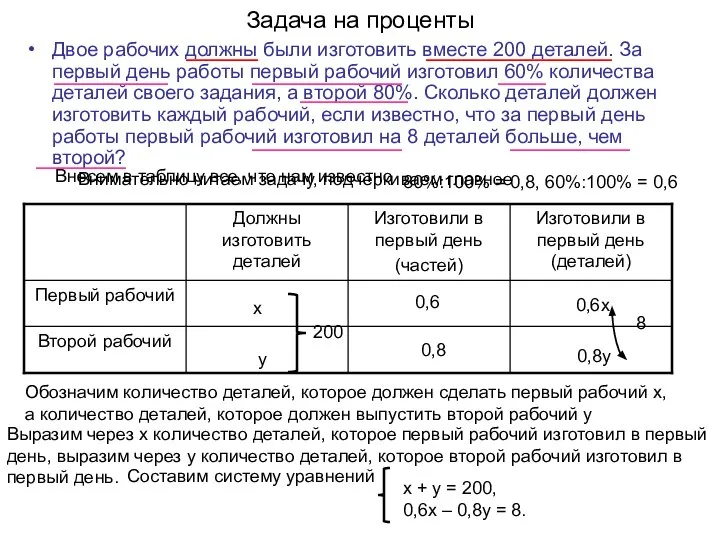
Внимательно читаем задачу, подчеркиваем главное
Внесем в таблицу все, что нам известно
200
80%:100% = 0,8, 60%:100% = 0,6
0,8
0,6
Обозначим количество деталей, которое должен сделать первый рабочий х,
а количество деталей, которое должен выпустить второй рабочий у
х
у
Выразим через х количество деталей, которое первый рабочий изготовил в первый день, выразим через у количество деталей, которое второй рабочий изготовил в первый день.
0,6х
0,8у
8
Составим систему уравнений
х + у = 200,
0,6х – 0,8у = 8.

Задача на сплавы
Имеется два сплава меди с другими металлами. Один сплав состоит из меди на 12%, а второй на 30%. Сколько килограммов каждого сплава надо взять, чтобы получить сплав массой 180 кг, состоящий на 25% из меди?
Внимательно читаем задачу, подчеркиваем главное
Внесем в таблицу все, что нам известно
Концентрация первого сплава 12%:100% = 0,12, концентрация второго сплава
30%:100% = 0,3, концентрация полученного сплава 25%:100% = 0,25.
0,12
0,3
0,25
180
Обозначим массу первого сплава х, а массу второго сплава у
х
у
Вычислим массу вещества в каждом сплаве, умножив массу сплава на концентрацию.
0,12х
0,3у
180 ∙ 0,25
Составим систему уравнений, учитывая что последний сплав получился при
сплавлении первых двух.
х + у = 180,
0,12х + 0,3у = 180 ∙ 0,25

Критерии оценивания работы
Минимальные программные требования: составить системы уравнений для задач №1, 2, 3, 4. решить одну из них.
На «4»: выполнить минимальные программные требования, решить задачу №5.
На «5»: выполнить минимальные программные требования, решить задачи №5, 6.

Задачи для самостоятельной работы
Имеется два сплава меди с другими металлами. Один сплав состоит из меди на 20%, а второй на 50%. Сколько килограммов каждого сплава надо взять, чтобы получить сплав массой 30 кг, состоящий на 30% из меди?
Имеется два водно-солевых раствора. Первый раствор содержит 35%, а второй 15% соли. Сколько граммов каждого раствора надо взять , чтобы получить 200 г раствора, содержащего 29% соли?
Есть два сплава, первый из которых содержит 30% меди, а второй – 70% меди. Сколько килограммов каждого сплава надо взять, чтобы получить 120 кг сплава, содержащего 40% меди?
Есть два раствора, первый из которых содержит 3% соли, а второй – 8% соли. Сколько граммов каждого раствора надо взять, чтобы получить 260 г раствора, содержащего 5% соли?