Задача 18. Готовимся к ЕГЭ

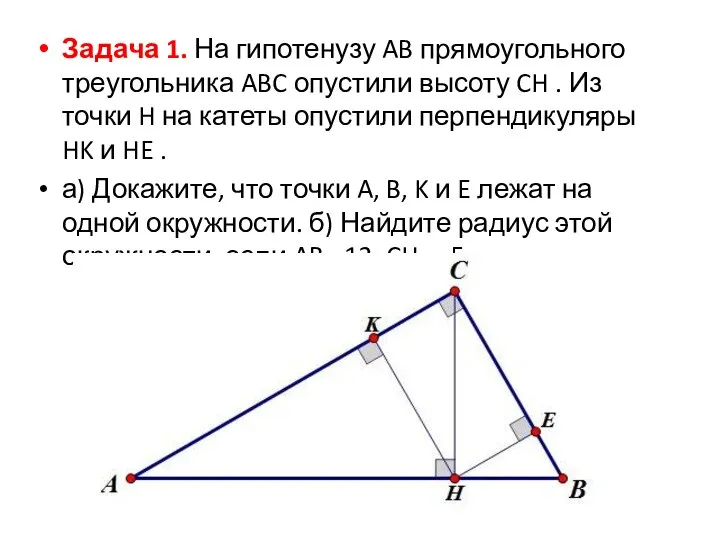
Задача 1. На гипотенузу AB прямоугольного треугольника ABC опустили высоту CH . Из точки H на катеты опустили перпендикуляры HK и HE .
а) Докажите, что точки A, B, K и E лежат на одной окружности. б) Найдите радиус этой окружности, если AB =12, CH = 5

а) Докажем, что четырехугольник AKEB можно вписать в окружность.
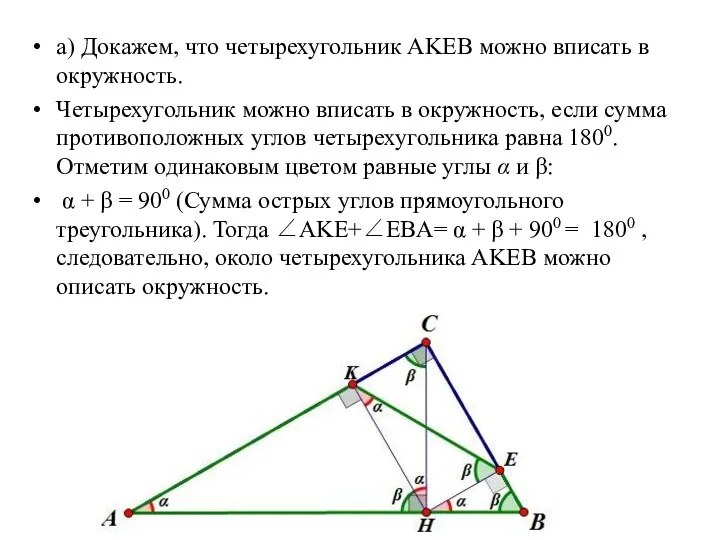
Четырехугольник можно вписать в окружность, если сумма противоположных углов четырехугольника равна 1800. Отметим одинаковым цветом равные углы α и β:
α + β = 900 (Сумма острых углов прямоугольного треугольника). Тогда ∠AKE+∠EBA= α + β + 900 = 1800 , следовательно, около четырехугольника AKEB можно описать окружность.

б)Начертим окружность, описанную около четырехугольника AKEB
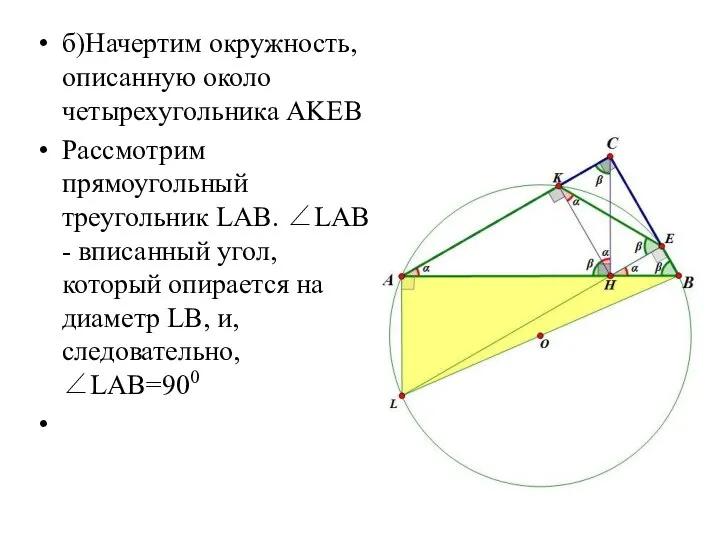
Рассмотрим прямоугольный треугольник LAB. ∠LAB - вписанный угол, который опирается на диаметр LB, и, следовательно, ∠LAB=900

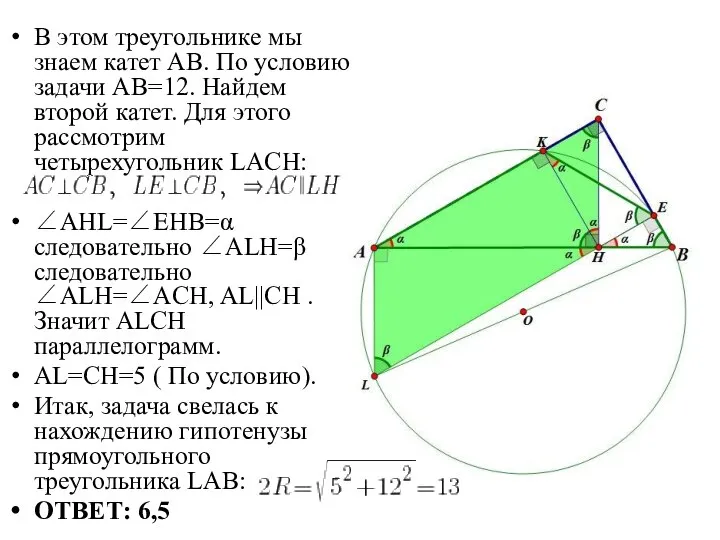
В этом треугольнике мы знаем катет АВ. По условию задачи АВ=12. Найдем второй катет. Для этого рассмотрим четырехугольник LACH:
∠AHL=∠EHB=α следовательно ∠ALH=β следовательно ∠ALH=∠ACH, AL||CH . Значит ALCH параллелограмм.
AL=CH=5 ( По условию).
Итак, задача свелась к нахождению гипотенузы прямоугольного треугольника LAB:
ОТВЕТ: 6,5

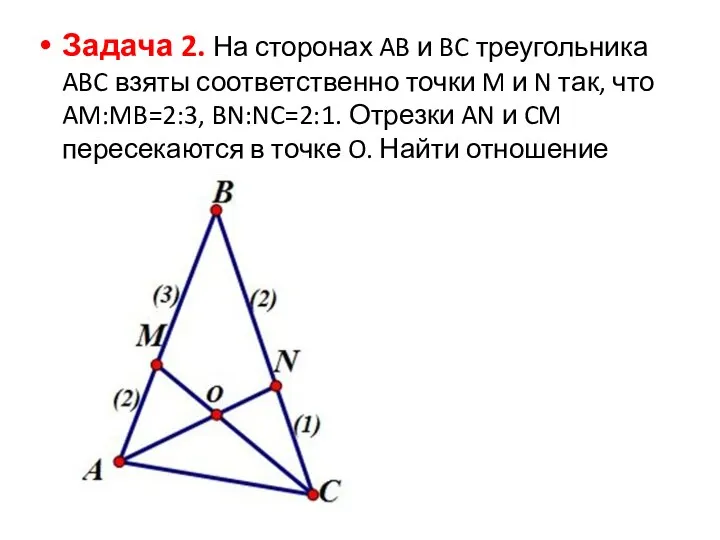
Задача 2. На сторонах AB и BC треугольника ABC взяты соответственно точки M и N так, что AM:MB=2:3, BN:NC=2:1. Отрезки AN и CM пересекаются в точке O. Найти отношение CO:OM.

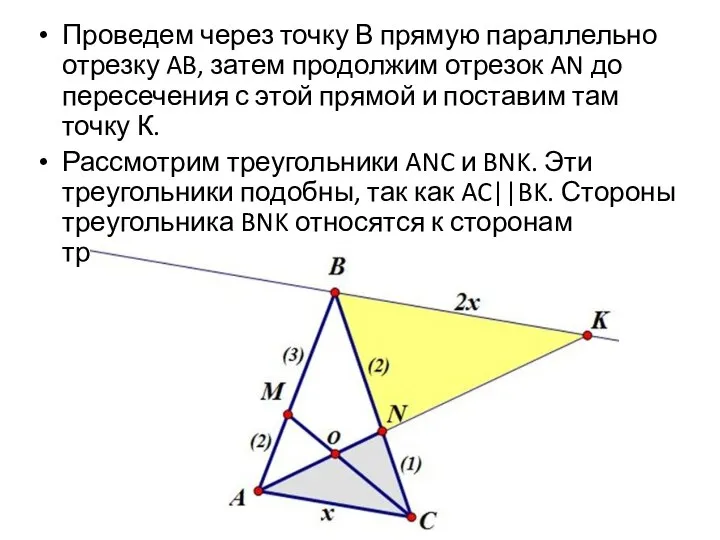
Проведем через точку В прямую параллельно отрезку AB, затем продолжим отрезок AN до пересечения с этой прямой и поставим там точку К.
Рассмотрим треугольники ANC и BNK. Эти треугольники подобны, так как AC||BK. Стороны треугольника BNK относятся к сторонам треугольника ANC как 2:1. Пусть AC=x, BK=2x.

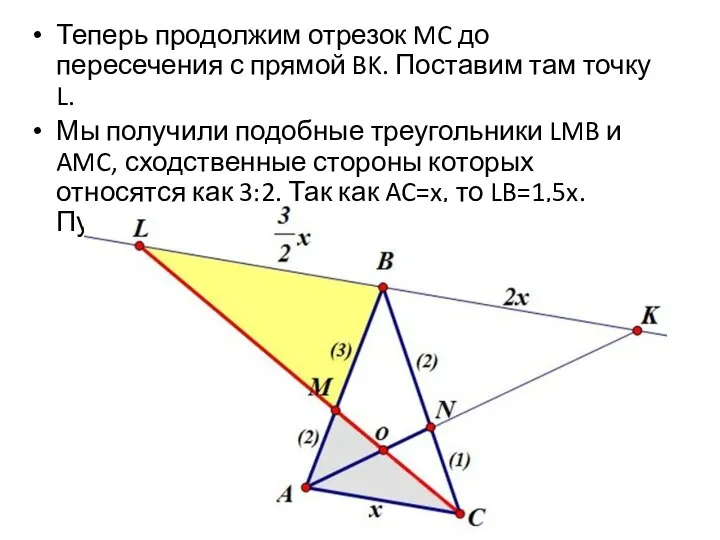
Теперь продолжим отрезок MC до пересечения с прямой BK. Поставим там точку L.
Мы получили подобные треугольники LMB и AMC, сходственные стороны которых относятся как 3:2. Так как AC=x, то LB=1,5x. Пусть LM=3n, MC=2n. Тогда LC=5n.

Теперь рассмотрим подобные треугольники LOK и AOC.
Тогда LO+OC=LC=4,5z.
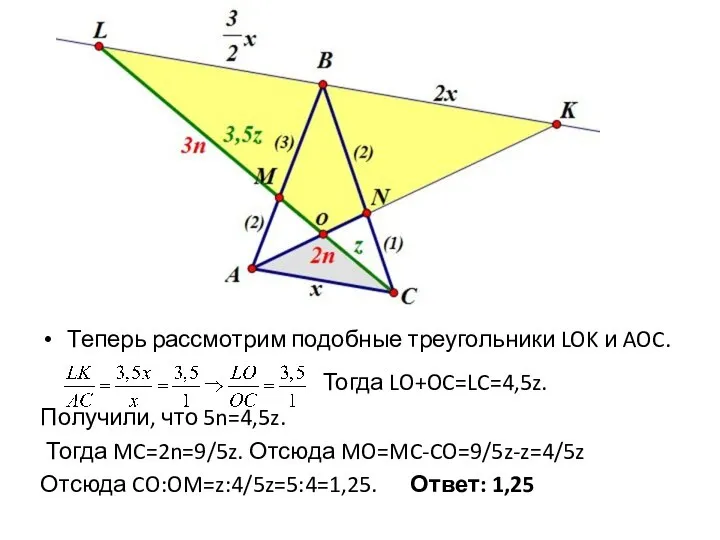
Получили, что 5n=4,5z.
Тогда MC=2n=9/5z. Отсюда MO=MC-CO=9/5z-z=4/5z
Отсюда CO:OM=z:4/5z=5:4=1,25. Ответ: 1,25

Теорема Менелая
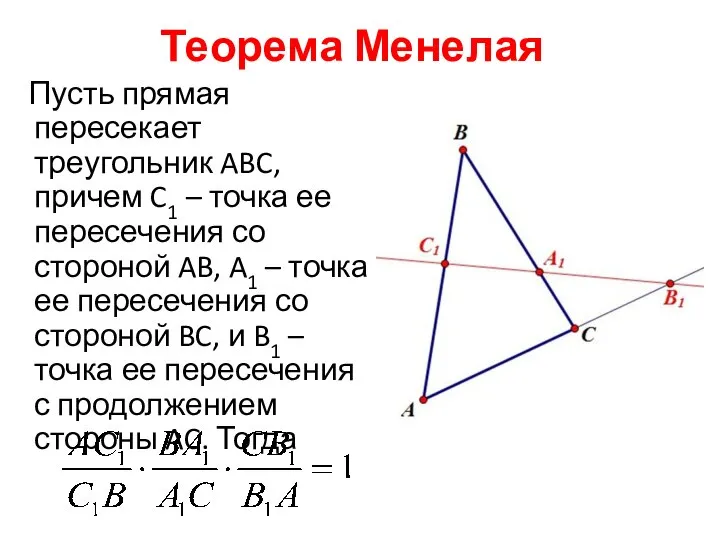
Пусть прямая пересекает треугольник ABC, причем C1 – точка ее пересечения со стороной AB, A1 – точка ее пересечения со стороной BC, и B1 – точка ее пересечения с продолжением стороны AC. Тогда