Решение простейших логарифмических логарифмических уравнений

Решить уравнение:
Log2 (x+3)=2
1.Найдём ОДЗ, учитывая , что логарифм определён только для положительных чисел.
Х+3>0
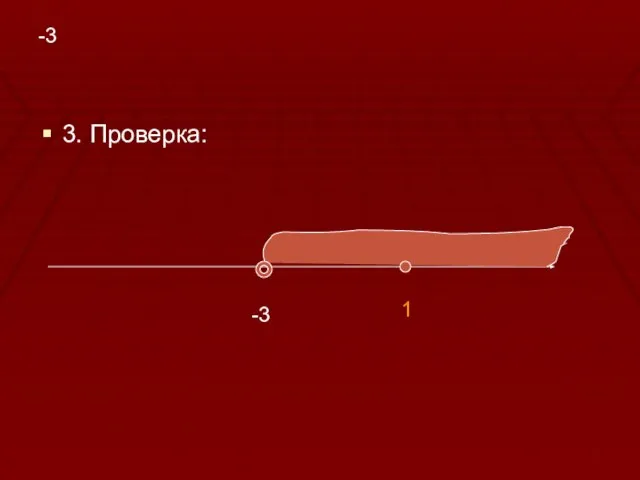
X>-3
-3

2.Решим уравнение:
Log2(x+3)=2 , 2 = Log222= Log2 4
Log2(x+3)=Log24
X+3=4
X=4-3
X=1

-3
3. Проверка:
-3
1

Ответ:1.

Решить уравнение:
Log0,3(4-x)=Log0,3(x+2).
1. Найдём ОДЗ уравнения:
Log0,3(4-x)=Log0,3 (x+2)

-2
-2
4
-2< x< 4

2. Решаем уравнение:
Log0,3(4-x)=Log0,3(2+x)
4 - x = 2+x
-2x=2-4
-2x = -2
X=1

3.Проверка.
-2
4
1
4.Ответ:1

Решить уравнение:
Logе(3х+7)- 2Loge(x+1)=0.

1.Найдём ОДЗ:
Logе(3х+7)- 2Loge(x+1)=0.

-1
X > -1
-1

2.Решаем уравнение:
Logе(3х+7)- 2Loge(x+1)=0.
Logе(3х+7)= 2Loge(x+1), 2Loge(x+1)= Loge(x+1)2
Loge(3x+7)=Loge(x+1)2
3x+7=(x+1)2
3x+7=x2 +2x +1
X2 +2x +1-3x -7=0
X2 –x – 6 =0
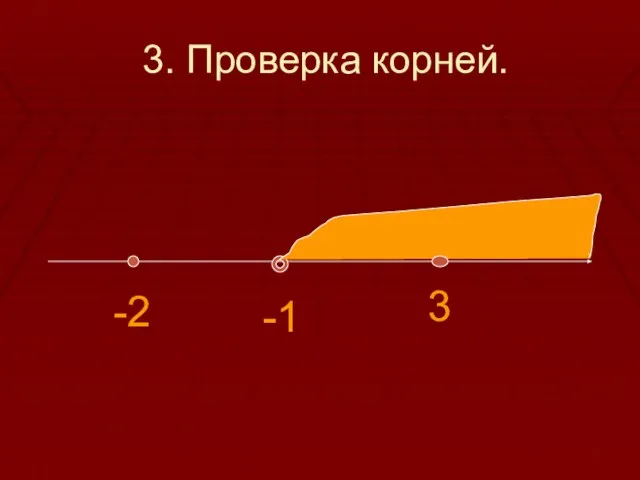
По теореме обратной Виета:х1 =3, х2 =-2

3. Проверка корней.
-1
3
-2

Ответ.3

Решить уравнение:
3Log3(1-x2)-Log3(1-x2)=4

1.Найдём ОДЗ:
3Log3(1-x2 ) - Log3(1-x2) =4.
1 - x2 >0,
X2 < 1,
|x|<1
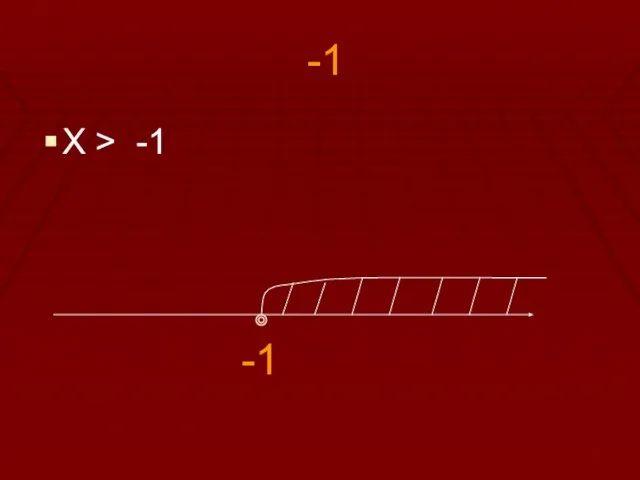
-1
1

2.Решим уравнение:
3Log3 2(1-x2)+Log3(1-x2) – 4 = 0,
Пусть Log3(1-x2)= t, тогда уравнение примет вид:
3t2 - t -4 =0,
т.к. а+в+с=0 , то t1= -1, t2 =-c\a= 4\3.
Получим: Log3(1-x2)=-1 или Log3(1-x2)=4/3
Log3(1-x2)=Log31/3 1- х2 = 34/3
1-x2 =1/3 х2 = 1-34/3 <0
х2=2/3 корней нет
х=

3.Проверка.
-1
1

Ответ .

Уравнения для самостоятельного решения.
Вариант 1.
1.log8(3x-2)=2
2.log0,99(5x-1)=log0,99(3x+7)
3.log54+log5(x-1)=log58
4.10lg(x-6)=x2 -12x +36
5. ln (x2-x)=ln(2x+4)
Вариант 2.
1.log7(5x+2)=1
2.lg(6x+1)=lg(-x+8)
3.log49+log4(x+1)=log43
4.eln(x-2)=x2 +6x -8
5. log2 (x2+3x)=log 2(x+3)