Исследование математических моделей

Пусть задана функция f(x). Требуется найти корни уравнения
f (x)=0 (1)
Задача нахождения корней уравнения (1) обычно решается в два этапа.
На первом этапе изучается расположение корней и проводится их разделение, то есть выделяются области, содержащие только один корень.
На втором этапе, используя начальное приближение, строится итерационный процесс для уточнений корня.

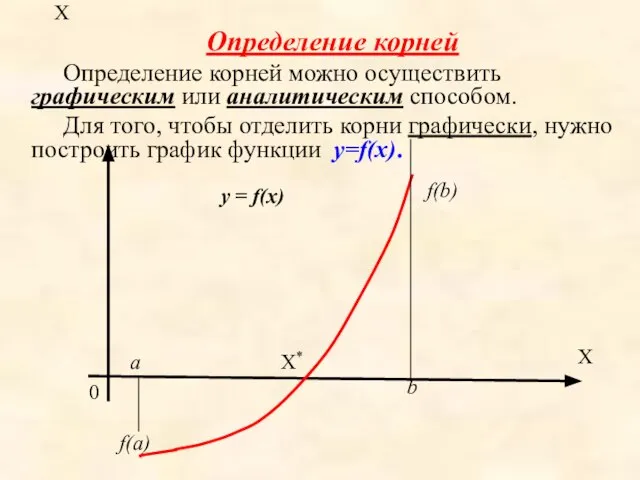
X
Определение корней
Определение корней можно осуществить графическим или аналитическим способом.
Для того, чтобы отделить корни графически, нужно построить график функции y=f(x).
X
0
a
b
f(a)
f(b)
X*
y = f(x)

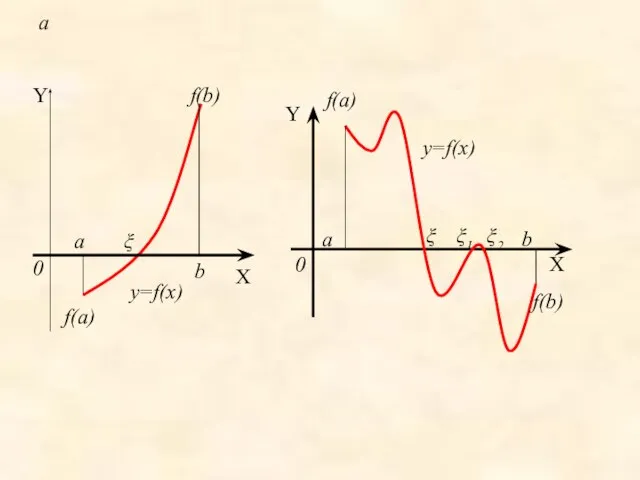
Для определения корней аналитически используем следующее утверждение:
если функция f(x) принимает значения разных знаков на концах отрезка [a, b], т.е.
f(a) f(b)<0,
то внутри этого отрезка содержится, по меньшей мере, один корень уравнения f(x)=0 .

a
a
ξ
b
0
X
Y
y=f(x)
f(a)
f(b)
0
Y
X
b
a
ξ
ξ1
f(a)
f(b)
y=f(x)
ξ2

Метод половинного деления
Предположим что в интервале [a, b] расположен один корень уравнения (1).
Найдем точку c= (b+a) /2. Это x0. Далее,
если f( c)* f( a) >0, то b = c,
если f( c)* f( b) >0, то a = c. Аналогично находим следующие приближения xn (n=1,2,…)
Если выполняется одно из условий :
| f(xn+1) | ≤ ε или | xn-xn+1 | ≤ ε,
где ε - заданная точность вычислений,
то корень уравнения f(x)=0 найден ξ=x*= xn+1 и процесс вычисления заканчивается.