Содержание
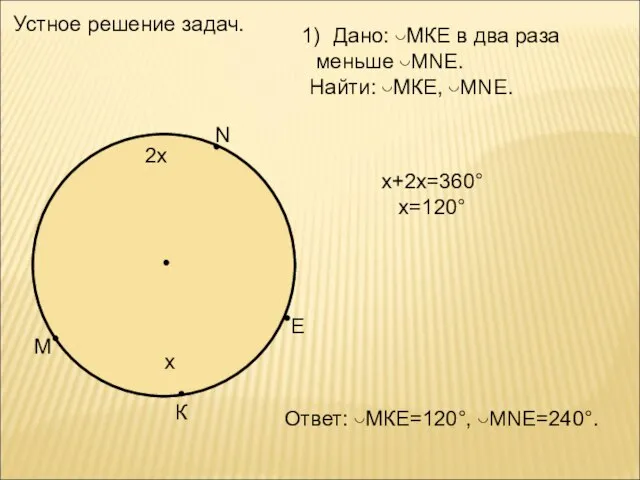
- 2. М К Е N Дано: ◡МКЕ в два раза меньше ◡MNE. Найти: ◡МКЕ, ◡MNE. х 2х
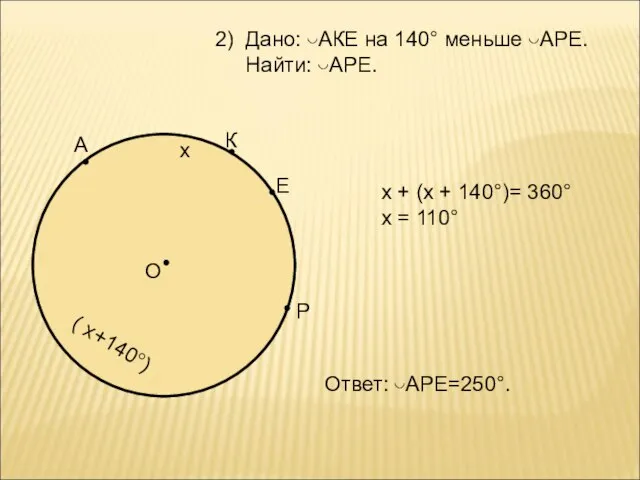
- 3. А К Е Р О Дано: ◡АКЕ на 140° меньше ◡АРЕ. Найти: ◡АРЕ. х ( х+140°)
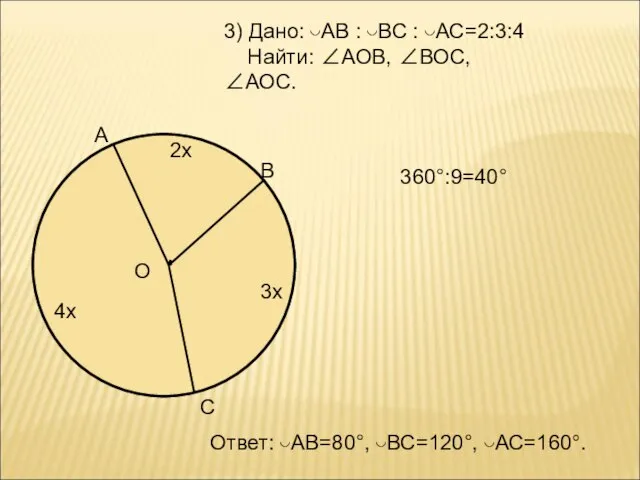
- 4. 3) Дано: ◡АВ : ◡ВС : ◡АС=2:3:4 Найти: ∠АОВ, ∠ВОС, ∠АОС. О А В С 2х
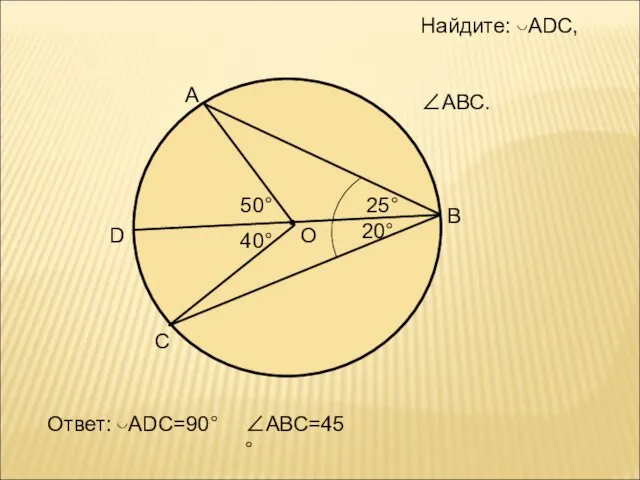
- 5. О В А С 50° 40° D Найдите: ◡АDС, ∠АВС. 25° 20° Ответ: ◡АDС=90° ∠АВС=45°
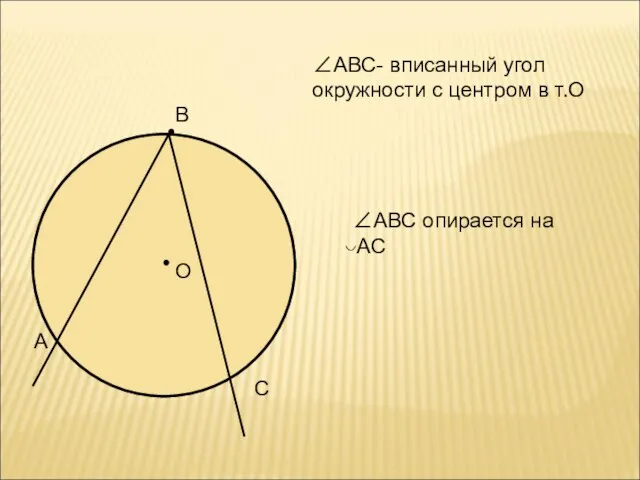
- 6. О В А С ∠АВС- вписанный угол окружности с центром в т.О ∠АВС опирается на ◡АС
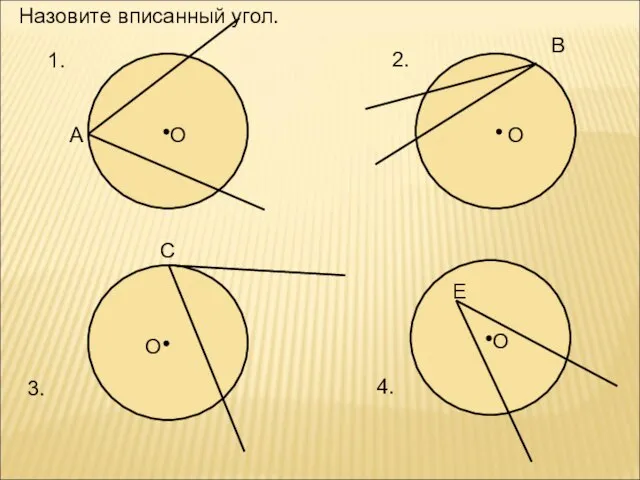
- 7. 1. 2. 3. 4. О О О О А В С Е Назовите вписанный угол.
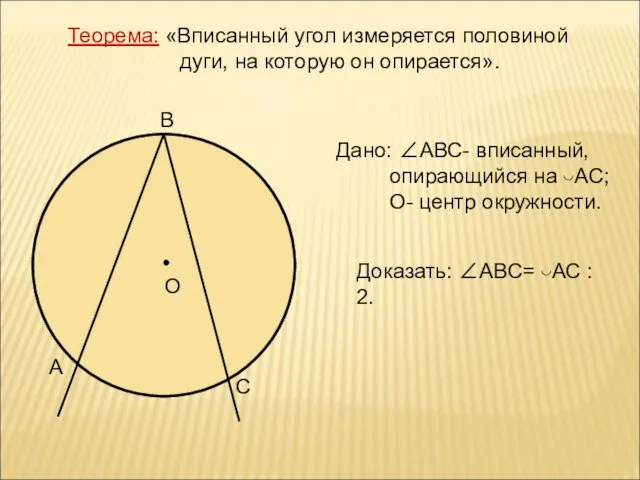
- 8. Теорема: «Вписанный угол измеряется половиной дуги, на которую он опирается». О А В С Дано: ∠АВС-
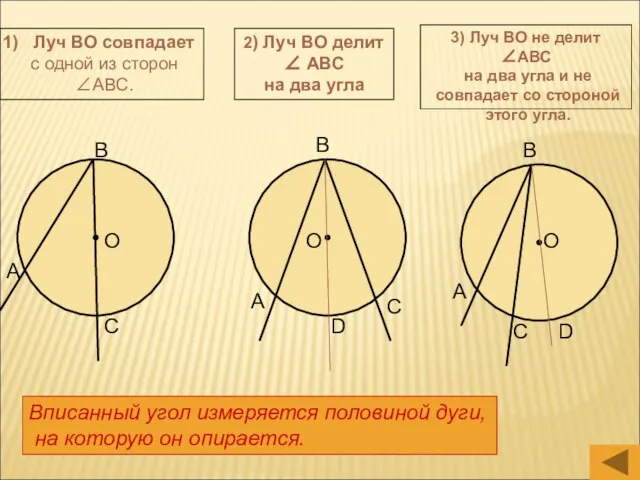
- 9. Луч ВО совпадает с одной из сторон ∠АВС. 2) Луч ВО делит ∠ АВС на два
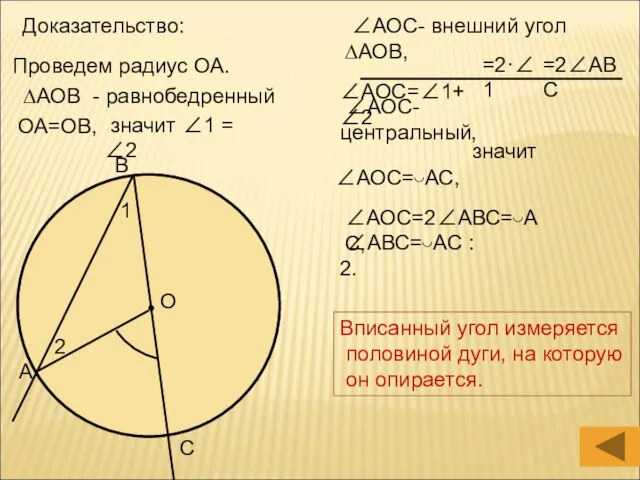
- 10. Доказательство: Проведем радиус ОА. ∆АОВ - равнобедренный ОА=ОВ, значит ∠1 = ∠2 О В А С
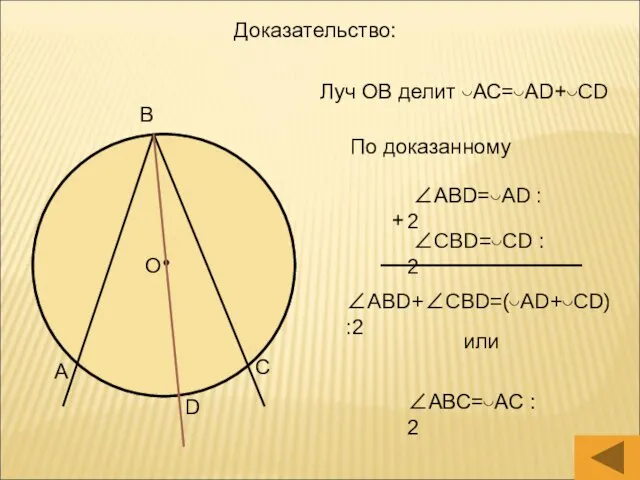
- 11. О А В С D Доказательство: Луч ОВ делит ◡АС=◡АD+◡CD По доказанному ∠АВD=◡AD : 2 ∠CBD=◡CD
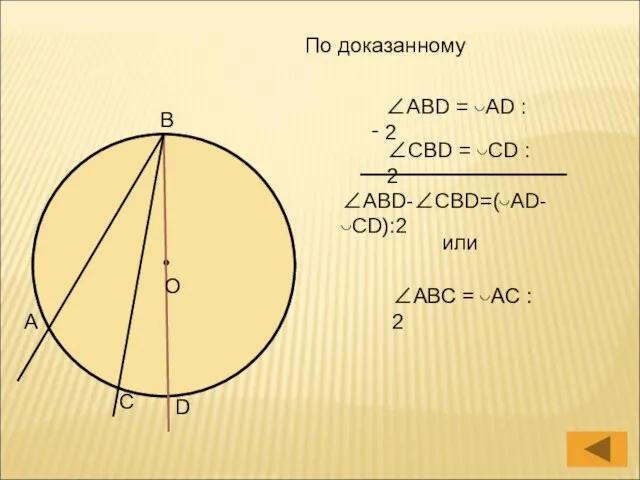
- 12. О А В С D По доказанному ∠ABD = ◡AD : 2 ∠CBD = ◡CD :
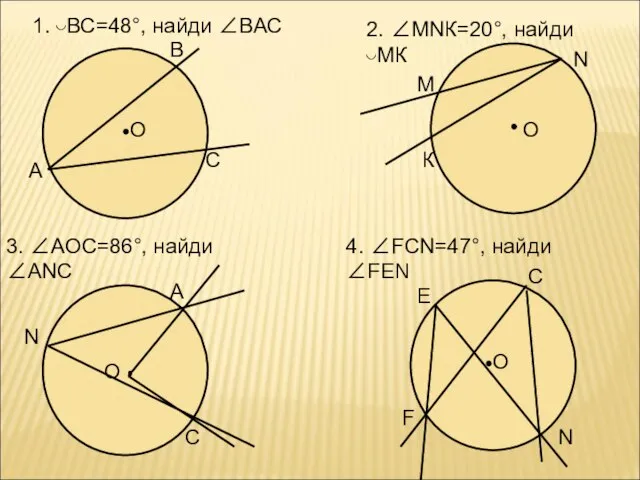
- 13. О А В С 1. ◡ВС=48°, найди ∠ВАС О М N К 2. ∠МNК=20°, найди ◡МК
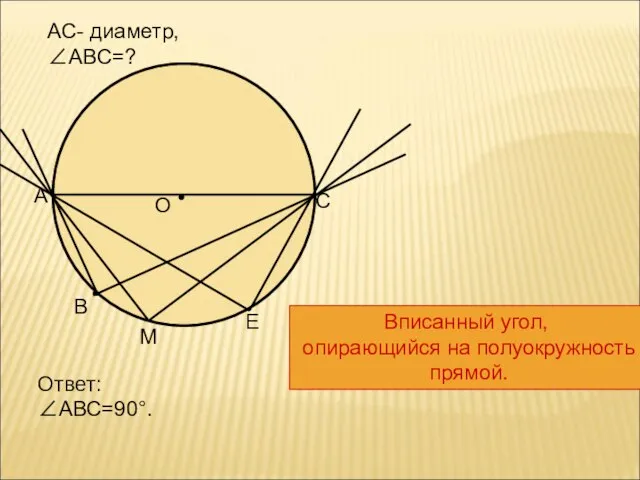
- 14. О В А С АС- диаметр, ∠АВС=? Ответ: ∠АВС=90°. М Е Вписанный угол, опирающийся на полуокружность
- 15. Решение задач: №656, №658.
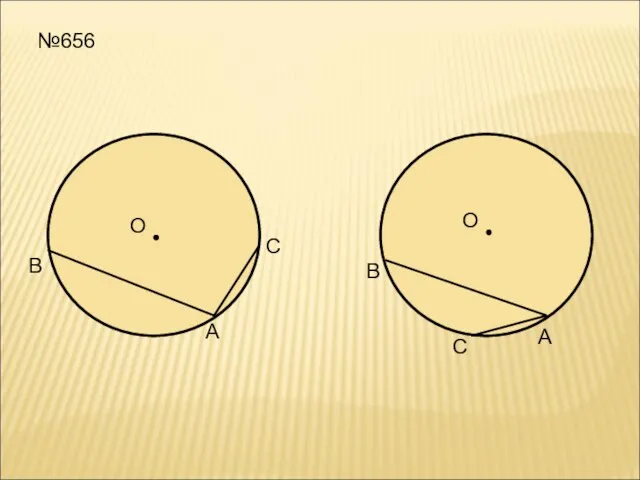
- 16. О В А С О А В С №656
- 17. О В А С Решение: ∠ВАС- вписанный, ∠ВАС= ◡ВС : 2. 115° 43° ◡ВС=360°-(115°+4°)=202°, значит ∠ВАС=101°
- 18. О В А С Решение: ∠ВАС- вписанный, ∠ВАС= ◡ВС : 2. 115° 43° ◡ВС=115° - 43°
- 19. №658.
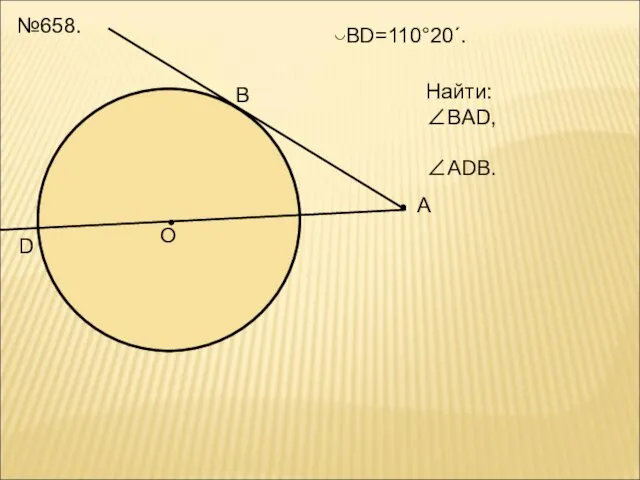
- 20. О В А D ◡BD=110°20´. Найти: ∠ВAD, ∠ADB. №658.
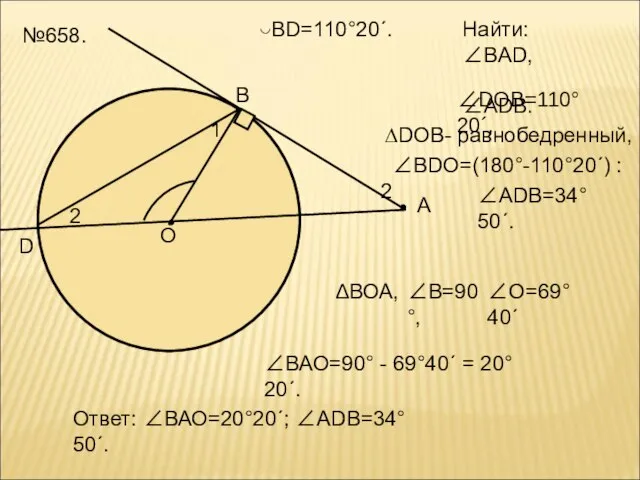
- 21. О В А D ◡BD=110°20´. Найти: ∠ВAD, ∠ADB. ∠DOB=110°20´, ∆DOB- равнобедренный, 1 2 ∠ВDО=(180°-110°20´) : 2
- 23. Скачать презентацию




 Медиана, биссектриса и высота треугольника
Медиана, биссектриса и высота треугольника Бумажные складные модели и их использование на уроках геометрии в 10 классе
Бумажные складные модели и их использование на уроках геометрии в 10 классе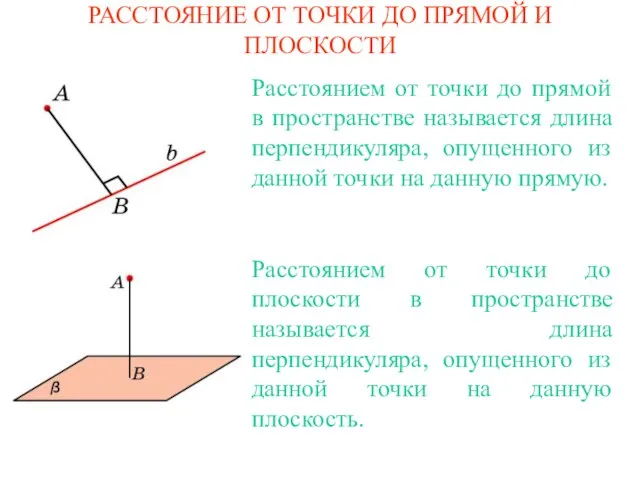 Расстояние от точки до прямой и плоскости
Расстояние от точки до прямой и плоскости Цилиндр. Конус. Шар
Цилиндр. Конус. Шар Признаки равенства треугольников
Признаки равенства треугольников Медианы, биссектрисы и высоты треугольника
Медианы, биссектрисы и высоты треугольника Фракталы и их применение в наши дни
Фракталы и их применение в наши дни Определение синуса, косинуса, тангенса и котангенса
Определение синуса, косинуса, тангенса и котангенса ВПИСАННЫЕ И ОПИСАННЫЕ ТРЕУГОЛЬНИКИ
ВПИСАННЫЕ И ОПИСАННЫЕ ТРЕУГОЛЬНИКИ Сумма углов треугольника 5 класс - презентация_
Сумма углов треугольника 5 класс - презентация_ Начертательная геометрия
Начертательная геометрия Графическое решение квадратных уравнений
Графическое решение квадратных уравнений Площадь прямоугольника
Площадь прямоугольника Вычисление угла между прямыми и плоскостями
Вычисление угла между прямыми и плоскостями Взаимное расположение прямых и плоскостей в пространстве
Взаимное расположение прямых и плоскостей в пространстве Свойство точек биссектрисы угла.
Свойство точек биссектрисы угла. Площадь трапеции
Площадь трапеции Доклад о «Сфере и шаре»
Доклад о «Сфере и шаре» Угол между плоскостями
Угол между плоскостями Геометрия крестово-купольного храма
Геометрия крестово-купольного храма ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности Площади плоских геометрических фигур
Площади плоских геометрических фигур Многогранники
Многогранники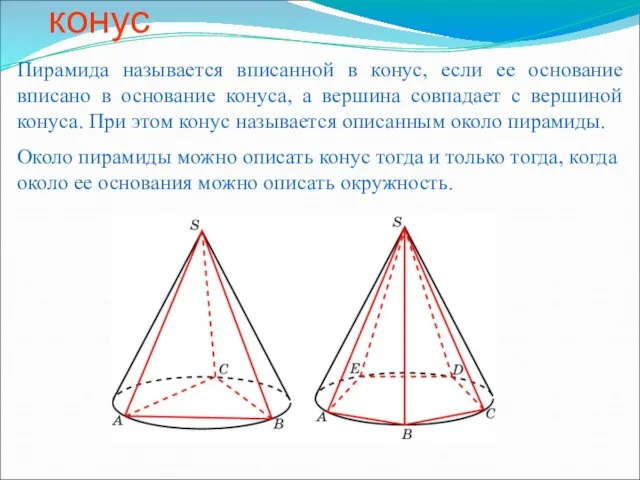 Пирамида, вписанная в конус
Пирамида, вписанная в конус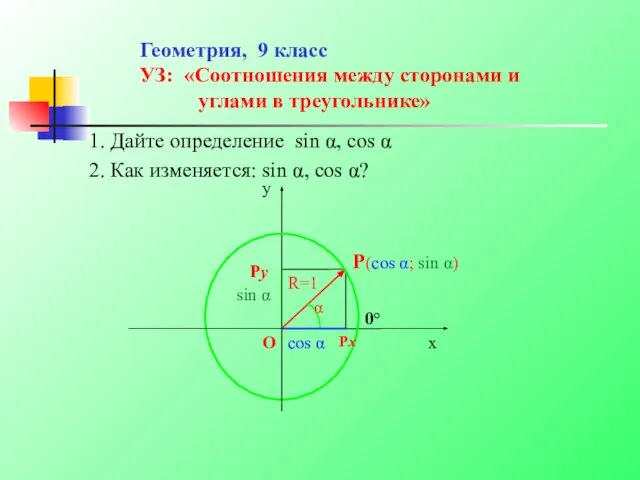 Соотношения между сторонами и углами в треугольнике
Соотношения между сторонами и углами в треугольнике Анализ геометрической формы предмета
Анализ геометрической формы предмета Золотое сечение в геометрии - презентация по Геометрии_
Золотое сечение в геометрии - презентация по Геометрии_ Теорема косинусов
Теорема косинусов