Слайд 2Формулировки и формула
Сформулируйте и запишите с помощью букв a, b и c

теорему Пифагора.
Сформулируйте теорему, обратную теореме Пифагора.
При решении каких задач применяются эти теоремы?
Слайд 3Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Применяется при нахождении
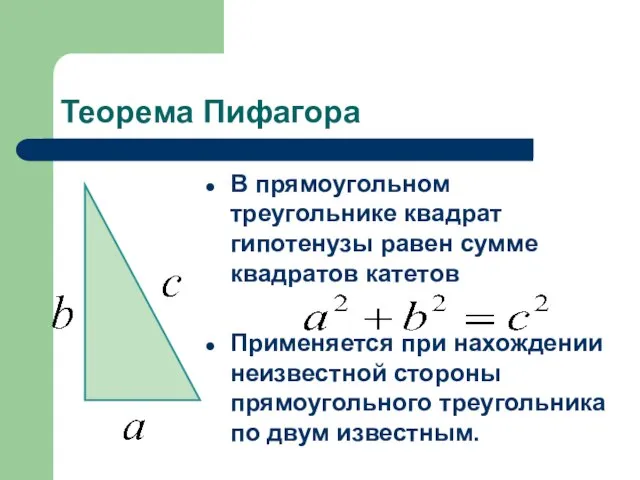
неизвестной стороны прямоугольного треугольника по двум известным.
Слайд 4Теорема, обратная теореме Пифагора
Если в треугольнике квадрат одной стороны равен сумме квадратов
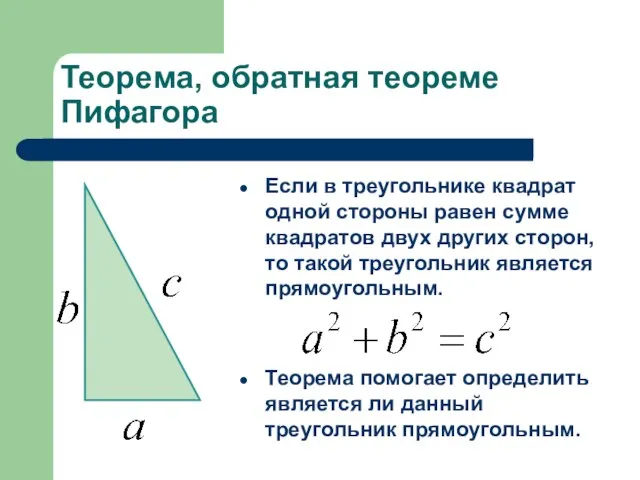
двух других сторон, то такой треугольник является прямоугольным.
Теорема помогает определить является ли данный треугольник прямоугольным.
Слайд 5Задача №1
В прямоугольном треугольнике катеты равны 6 см и 8 см. Чему

равна гипотенуза?
Слайд 6Задача №2
В прямоугольном треугольнике гипотенуза равна 13 см, а один из катетов
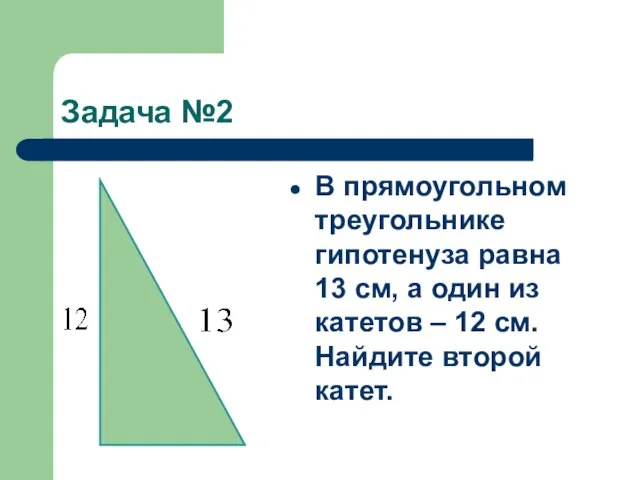
– 12 см. Найдите второй катет.
Слайд 7Задача №3
Определите, является ли прямоугольным треугольник со сторонами 8 м, 5

м и 9 м.
Слайд 8Задача №4
В треугольнике две стороны равны соответственно 20 см и 15 см.

Какой должна быть большая сторона, чтобы треугольник был прямоугольным?
Слайд 9Задача №5
Диагонали ромба равны 16 см и 12 см. Вычислите: а) сторону
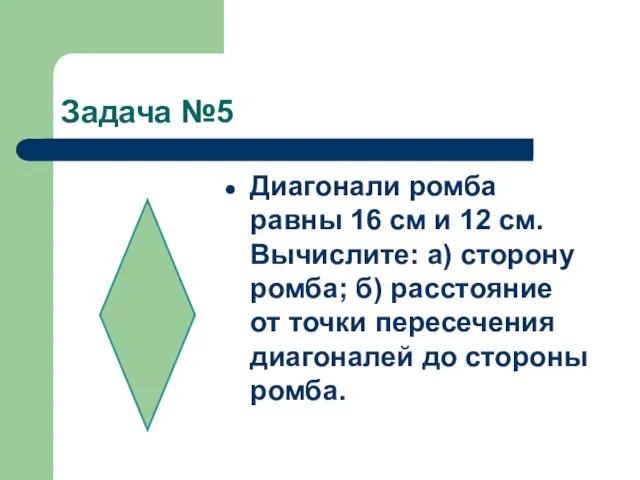
ромба; б) расстояние от точки пересечения диагоналей до стороны ромба.
Слайд 10Задача №6
В прямоугольной трапеции большая боковая сторона и меньшая диагональ равны по

13 см, а меньшее основание 12 см. Вычислите: а) высоту трапеции; б) большую диагональ.









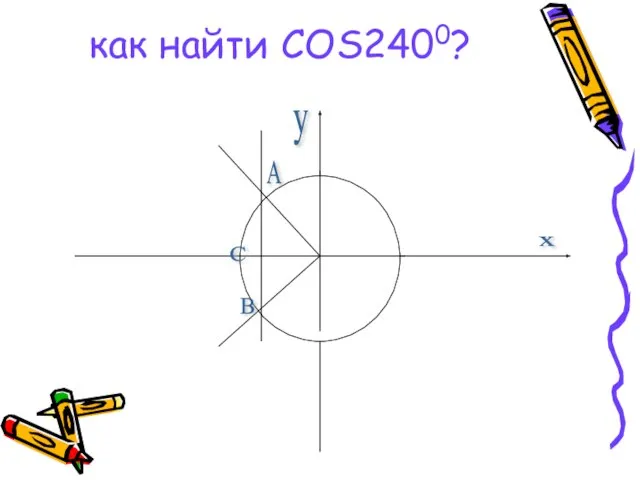 Косинус
Косинус Итоговое повторение курса геометрии
Итоговое повторение курса геометрии Цилиндр и конус
Цилиндр и конус Преобразования на плоскости
Преобразования на плоскости ПРОПОРЦИОНАЛЬНОСТЬ Учитель Ибрагимова Т.И. ГБОУ школа №212 Фрунзенского района Санкт-Петербурга
ПРОПОРЦИОНАЛЬНОСТЬ Учитель Ибрагимова Т.И. ГБОУ школа №212 Фрунзенского района Санкт-Петербурга Правильный додекаэдр
Правильный додекаэдр Основные формулы тригонометрии
Основные формулы тригонометрии Свойство биссектрисы угла треугольника
Свойство биссектрисы угла треугольника Векторы 9 класс
Векторы 9 класс В гостях у Геометрии - презентация по Геометрии_
В гостях у Геометрии - презентация по Геометрии_ вид разреза сечения
вид разреза сечения Окружность в аксонометрии
Окружность в аксонометрии Параллельность в пространстве
Параллельность в пространстве Биссектриса угла
Биссектриса угла Правильные многогранники
Правильные многогранники Соотношения между сторонами и углами прямоугольного треугольника (Подготовка к контрольной работе)
Соотношения между сторонами и углами прямоугольного треугольника (Подготовка к контрольной работе) Площади и объемы - презентация по Геометрии_
Площади и объемы - презентация по Геометрии_ Геометрические фигуры (Взаимное расположение на плоскости)
Геометрические фигуры (Взаимное расположение на плоскости) Приготовьтесь к построению
Приготовьтесь к построению План –конспект урока. Тема: «Треугольник» 5 класс.
План –конспект урока. Тема: «Треугольник» 5 класс. ЭЛЛИПС
ЭЛЛИПС Свойства производной. Построение графиков функций. (Повторение материала 10 класса).
Свойства производной. Построение графиков функций. (Повторение материала 10 класса). Сумма двух векторов Геометрия -9 Урок 4
Сумма двух векторов Геометрия -9 Урок 4 Курсовая работа слушателя курсов «Информационно - коммуникационное сопровождение обучения математике» Савицкой Галины Ивановны
Курсовая работа слушателя курсов «Информационно - коммуникационное сопровождение обучения математике» Савицкой Галины Ивановны Почему квадрат?
Почему квадрат? Теорема синусов 9 класс
Теорема синусов 9 класс Свойство и признак описанного четырёхугольника
Свойство и признак описанного четырёхугольника Планиметрия - презентация по Геометрии_
Планиметрия - презентация по Геометрии_