И.Р.Высоцкий, Д.Д.Гущин, П.И.Захаров и др.; под ред. А.Л.Семенова, И.В.Ященко. – М.:АСТ:Астрель, 2010. – 93, (3)с. – (Федеральный институт педагогических измерений)
Математика: тематическое планирование уроков подготовки к экзамену / Белошистая.В. А. –М: Издательство «Экзамен», 2007. – 478 (2) с. (Серия «ЕГЭ 2007. Поурочное планирование»)
Математика: самостоятельная подготовка к ЕГЭ / Л.Д. Лаппо, М.А. Попов. – 3-е изд., перераб. И дополн. - М.: Издательство «Экзамен», 2009. – 381, (3) с. (Серия «ЕГЭ. Интенсив»)
Математика. Решение задач группы В / Ю.А.Глазков, И.А.Варшавский, М.Я. Гаиашвилли. – М.: Издательство «Экзамен», 2009. – 382 (2) с. (Серия «ЕГЭ. 100 баллов»)
Математика: тренировочные тематические задания повышенной сложности с ответами для подготовки к ЕГЭ и к другим формам выпускного и вступительного экзаменов /сост Г.И.Ковалева, Т.И.Бузулина, О.Л.Безрукова, Ю.А. Розка. _ Волгоград: Учитель, 20089, - 494 с.
Шабунин М.И. и др. Алгебра и начала анализа: Дидактические материалы для 10-11 кл. – 3-е изд. – М.: Мнемозина, 2000. – 251 с.: ил.
Список рекомендуемой литературы




 Софт- портфель учителя
Софт- портфель учителя Одночлены. Многочлены. 7 класс
Одночлены. Многочлены. 7 класс Наглядная геометрия
Наглядная геометрия Разряды чисел
Разряды чисел Умножение и деление натуральных чисел
Умножение и деление натуральных чисел Решение задач
Решение задач Функции y=x2 и y=x3 и их графики
Функции y=x2 и y=x3 и их графики Занимательный устный счет
Занимательный устный счет Замена переменных в определенном интеграле. Лекция №9
Замена переменных в определенном интеграле. Лекция №9 Линейное уравнение с одной переменной. Урок 15
Линейное уравнение с одной переменной. Урок 15 Непрерывность функции на отрезке
Непрерывность функции на отрезке 32046
32046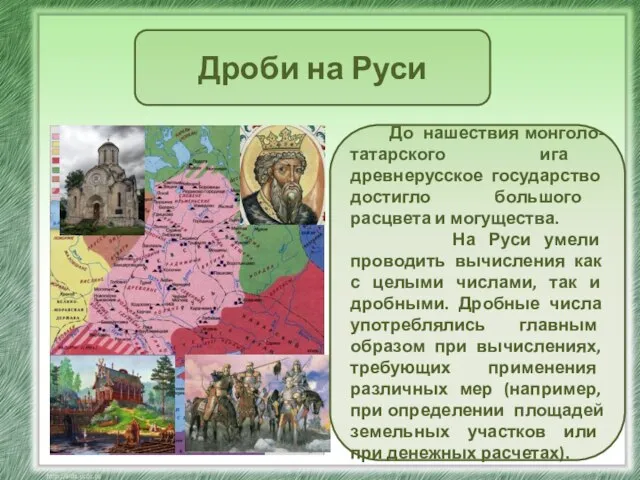 Презентация по математике "Дроби на Руси" -
Презентация по математике "Дроби на Руси" -  Построение фронтальной диметрической и изометрической проекций
Построение фронтальной диметрической и изометрической проекций Проецирование точки
Проецирование точки 2. Свойства параллелограмма
2. Свойства параллелограмма Мой кабинет – моя лаборатория Презентацию подготовила заведующая школьным кабинетом математики №14 Ларионова Татьяна Ивановна.
Мой кабинет – моя лаборатория Презентацию подготовила заведующая школьным кабинетом математики №14 Ларионова Татьяна Ивановна. Системы уравнений. Основные понятия
Системы уравнений. Основные понятия Римская нумерация
Римская нумерация Деление круглых сотен на число 100
Деление круглых сотен на число 100 Параллельные прямые. Тест
Параллельные прямые. Тест Площадь параллелограмма
Площадь параллелограмма Автоматизация ректификационной колонны К-2 установки сернокислотного алкилирования Л-25/7
Автоматизация ректификационной колонны К-2 установки сернокислотного алкилирования Л-25/7 Прямоугольный треугольник
Прямоугольный треугольник Комплексные числа
Комплексные числа Стандартизированные коэффициенты регрессии
Стандартизированные коэффициенты регрессии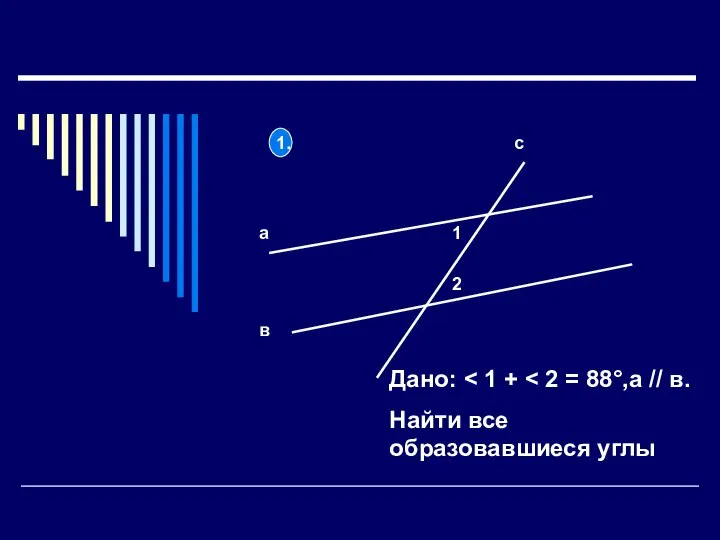 Признаки равенства треугольников
Признаки равенства треугольников Осевая и центральная симметрии
Осевая и центральная симметрии