Слайд 11Игра «Художник»
Цель игры: Отработать умение строить точку по заданным координатам.
Задание: Построить фигуру,

соединяя, по мере построения, соседние точки друг с другом. Далее даются координаты точек, например следующие:
(4; - 3), (2; - 3), (2; - 2), (4; -2), (4; - 1), (3; 1), (2; 1), (1; 2), (0; 0), (- 3; 2), (- 4; 5), (0; 8), (2; 7),
(6; 7), (8; 8), (10; 6), (10; 2), (7; 0), (6; 2), (6; - 2), (5; - 3), (4; - 3), (4; - 5), (3; - 9),(0; - 8), (1; - 5), (1; - 4), (0; - 4), (0; - 9), (- 3; - 9), (- 3; - 3), (- 7; - 3), (- 7; - 7),(- 8; - 8), (-11; - 8), (- 10; - 4),
(- 11; - 1), (- 14; - 3), (- 12; -1), (- 11; 2), (- 8; 4), (-4; 5).
Далее отдельно строятся две точки: (2; 4), (6; 4).
В результате получается определенный рисунок. В данном случае это «слоник».












 Приём вычислений вида 35 - 7. 2 класс
Приём вычислений вида 35 - 7. 2 класс Степень с рациональным показателем. 11 класс
Степень с рациональным показателем. 11 класс Мотивация … Статистика
Мотивация … Статистика Упрощение выражений. Восстановите цепочку вычислений
Упрощение выражений. Восстановите цепочку вычислений Величины. Длина
Величины. Длина Интерактивный тренажер Подобные слагаемые
Интерактивный тренажер Подобные слагаемые 2Урок обобщения и систематизации знаний. Определение логарифма числа по основанию
2Урок обобщения и систематизации знаний. Определение логарифма числа по основанию Презентация на тему Нахождение дроби от числа. Нахождение числа
Презентация на тему Нахождение дроби от числа. Нахождение числа  Параллельные прямые в пространстве
Параллельные прямые в пространстве Основы геометрии (5 класс)
Основы геометрии (5 класс) Экстремум функции. Признак постоянства функции. Исследование на экстремум
Экстремум функции. Признак постоянства функции. Исследование на экстремум Равносильность формул
Равносильность формул Аналитическая геометрия на плоскости (лекция 1-2)
Аналитическая геометрия на плоскости (лекция 1-2) Пространственные тела. Многогранники
Пространственные тела. Многогранники Приближенное решение уравнений
Приближенное решение уравнений Понятие вектора в пространстве
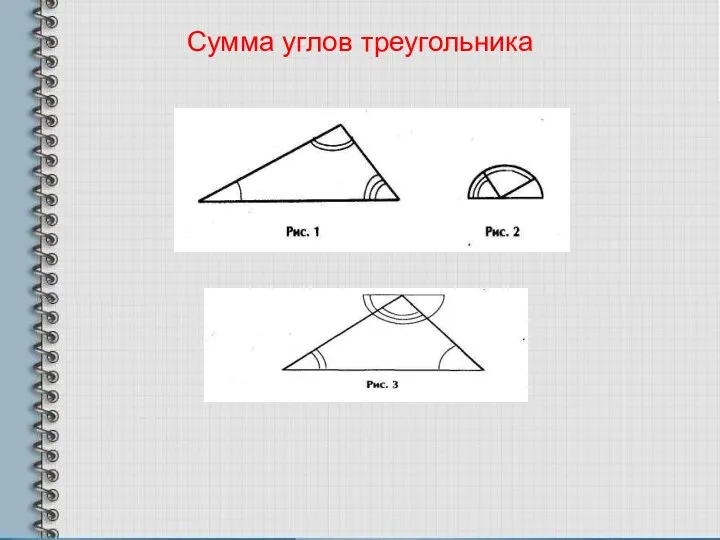
Понятие вектора в пространстве Сумма углов в треугольнике
Сумма углов в треугольнике Тригонометрия – математическая дисциплина. Синус, косинус, тангенс и котангенс угла (10 класс)
Тригонометрия – математическая дисциплина. Синус, косинус, тангенс и котангенс угла (10 класс) Соединения с повторениями
Соединения с повторениями Функция
Функция ЕГЭ Профиль. Решение задания №12
ЕГЭ Профиль. Решение задания №12 Применение тактильных приемов при изучении геометрического материала в 5 классе
Применение тактильных приемов при изучении геометрического материала в 5 классе Компьютерный и интеллектуальный анализ данных. Теория вероятностей
Компьютерный и интеллектуальный анализ данных. Теория вероятностей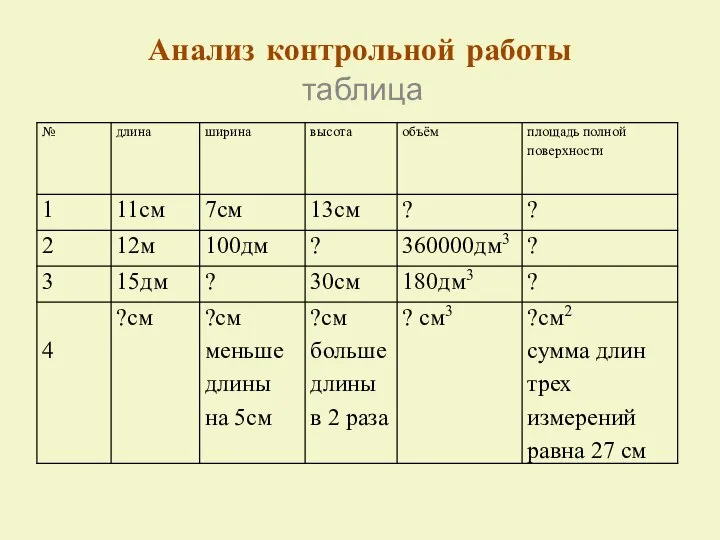 Таблицы и диаграммы. Чтение и составление таблиц
Таблицы и диаграммы. Чтение и составление таблиц Понятие цилиндра
Понятие цилиндра Преобразование графиков функций. 8 класс
Преобразование графиков функций. 8 класс Типи трикутників
Типи трикутників Производные функции нескольких переменных (часть 1)
Производные функции нескольких переменных (часть 1)