Ряды динамики

Понятие рядов динамики
Dr. Igor Arzhenovskiy
Статистика
Ряд динамики (или временной, или хронологический ряд – это ряд чисел, характеризующих развитие явления во времени:
У каждого ряда динамики имеются два элемента: уровень ряда y и
момент (период) времени t.
Различают два вида рядов динамики:
моментный ряд дает сведения о развитии явления на какие-то после-
довательные моменты времени (пример: численность населения на
1.01.2012 г.)
интервальный ряд дает сведения о развитии явления за определенные
периоды времени (пример: выпуск продукции за квартал)
Анализ рядов динамики предполагает решение следующих задач:
- определение среднего уровня ряда;
- определение темпов роста и прироста;
- определение тренда;
- определение сезонной компоненты;
преобразование рядов: сглаживание, выравнивание, смыкание и т.д.

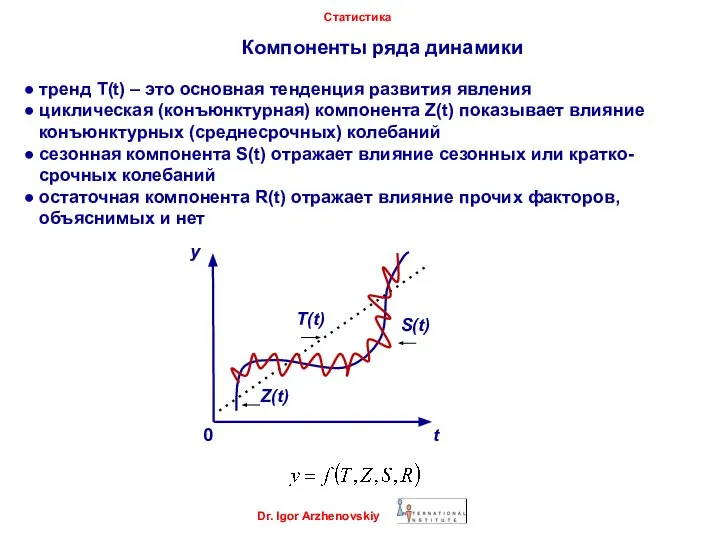
Компоненты ряда динамики
Dr. Igor Arzhenovskiy
Статистика
● тренд T(t) – это основная тенденция развития явления
● циклическая (конъюнктурная) компонента Z(t) показывает влияние
конъюнктурных (среднесрочных) колебаний
● сезонная компонента S(t) отражает влияние сезонных или кратко-
срочных колебаний
● остаточная компонента R(t) отражает влияние прочих факторов,
объяснимых и нет
y
Z(t)
S(t)
T(t)
0 t

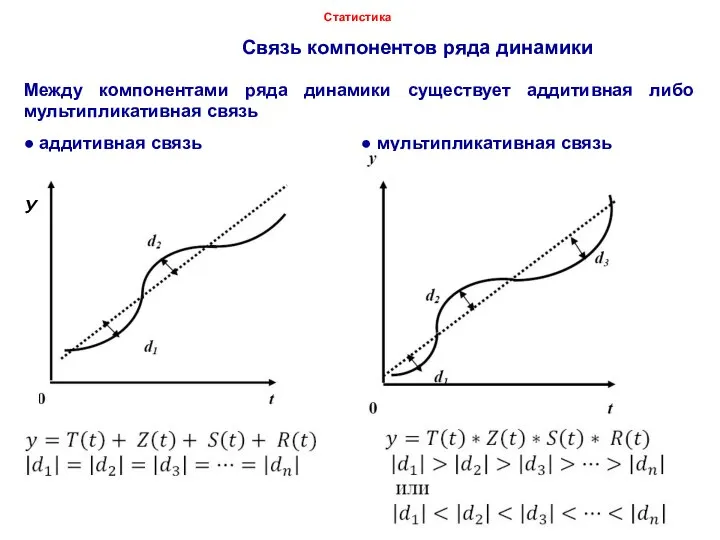
Связь компонентов ряда динамики
Статистика
Между компонентами ряда динамики существует аддитивная либо мультипликативная связь
● аддитивная связь ● мультипликативная связь
У

Показатели ряда динамики
Статистика
● Начальный уровень ряда
● Конечный уровень ряда
● Средний уровень ряда
Для интервального ряда средний уровень рассчитывается по средне-
арифметической простой и взвешенной:
где n – число уровней;
ti – длительность интервала времени между уровнями.
Пример: Предприятие выпускает продукцию по кварталам года:
I кв. – 300 тыс. руб.,
II кв.– 250 тыс. руб.,
III кв.– 100 тыс. руб.,
IV кв.– 500 тыс. руб.
Средний уровень интервального ряда с равноотстоящими интервалами:
Dr. Igor Arzhenovskiy

Показатели ряда динамики
Статистика
● Начальный уровень ряда
● Конечный уровень ряда
● Средний уровень ряда
Для интервального ряда средний уровень рассчитывается по средне-
арифметической простой и взвешенной:
где n – число уровней;
ti – длительность интервала времени между уровнями.
Пример 1: Предприятие выпускает продукцию по кварталам года:
I кв. – 300 тыс. руб.,
II кв.– 250 тыс. руб.,
III кв.– 100 тыс. руб.,
IV кв.– 500 тыс. руб.
Средний уровень интервального ряда с равноотстоящими интервалами:
Dr. Igor Arzhenovskiy

Пример 2: Предприятие выпустило продукции за первые 3 месяца года на 300 тыс. руб.,
за последующие 2 месяца – на 250 тыс. руб., за 1 месяц – на 100 тыс. руб. и
за оставшиеся 6 месяцев – на 500 тыс. руб.
Средний уровень интервального ряда с неравноотстоящими интервалами:
Dr. Igor Arzhenovskiy
Статистика

Dr. Igor Arzhenovskiy
Статистика
Для моментного ряда c равноотстоящими интервалами средний уровень исчисляется по формуле средней хронологической:
Пример: остатки оборотных средств предприятия составили:
на 1.01 – 110 тыс. руб.,
на 1.02 – 120 тыс. руб.,
на 1.03 – 130 тыс. руб.,
на 1.04 – 140 тыс. руб.,
на 1.07 – 170 тыс. руб.
Определим средние остатки оборотных средств за I квартал:

Dr. Igor Arzhenovskiy
Статистика
Для моментного ряда с неравноотстоящими интервалами применяют формулу средней хронологической взвешенной:
В нашем примере средние остатки оборотных средств за полугодие:

Dr. Igor Arzhenovskiy
Статистика
Темпы роста и прироста
Коэффициент роста отвечает на вопрос, во сколько раз изменилось
явление. Коэффициент роста, выраженный в процентах, называют темпом роста.
Коэффициент прироста отвечает на вопрос, на сколько увеличилось явление. Коэффициент прироста, выраженный в процентах, называют темпом прироста.
Средний коэффициент роста находится по средней геометрической:
Пример: фирма произвела услуг в 1 году – на 100 у.е., во 2 году – на 120 у.е., в 3 году – на 132 у.е. и в 4 году – на 200 у.е.

Dr. Igor Arzhenovskiy
Статистика
Правила составления рядов динамики
1. Все уровни динамического ряда должны быть сопоставимыми во времени.
Пример: численность населения обычно указывается на начало года
2. Все уровни динамического ряда должны быть сопоставимыми в пространстве, т.е. относиться к одной и той же территории
Пример: в 1993 г. в состав Нижегородской области вошел Сокольский район Ивановской области
3. Все уровни динамического ряда должны быть сопоставимыми по методологии расчета.
Пример: для составления динамического ряда ВВП данные по производству совокупного общественного продукта (СОП), рассчитывавшегося до начала 90-х годов, пересчитываются в ВВП.

Dr. Igor Arzhenovskiy
Статистика
Преобразование рядов динамики
Сглаживание и выравнивание ряда
1. Выявление тренда визуальным методом (на графике). Этот метод
наиболее прост и наименее точен.
2. Механическое выравнивание, т.е. укрупнение интервалов путем
расчета средних уровней не за один период, а за несколько.
Пример: средняя урожайность не за 1 год, а за 5 лет
Недостаток метода: потеря значительного числа уровней ряда и его
укорачивание.
3. Метод скользящей средней, т.е. замена несколько уровней одним
значением. Недостаток метода: теряются уровни в начале и в конце
ряда, центрирование при чётном интервале сглаживания
Пример: интервал сглаживания – 3 месяца
и т.д.

Dr. Igor Arzhenovskiy
Статистика
Преобразование рядов динамики
Сглаживание и выравнивание ряда
Сведения о продажах продукции по месяцам на предприятии N
4. Аналитическое выравнивание. Фактические уровни заменяются
уровнями, вычисленными на основе определенной функции (кривой)
регрессии (прямой, гиперболы, параболы, показательной, экспонен-
циальной и других функций.
Пример: линейная зависимость продаж от времени
или

Dr. Igor Arzhenovskiy
Статистика
Преобразование рядов динамики
Сглаживание и выравнивание ряда
Уравнение регрессии:
Выровненные значения y:
и т.д.
Сезонная компонента:
и т.д.
Расчет отдельных уровней ряда (интерполяция и экстраполяция).
Пример: для t = 4

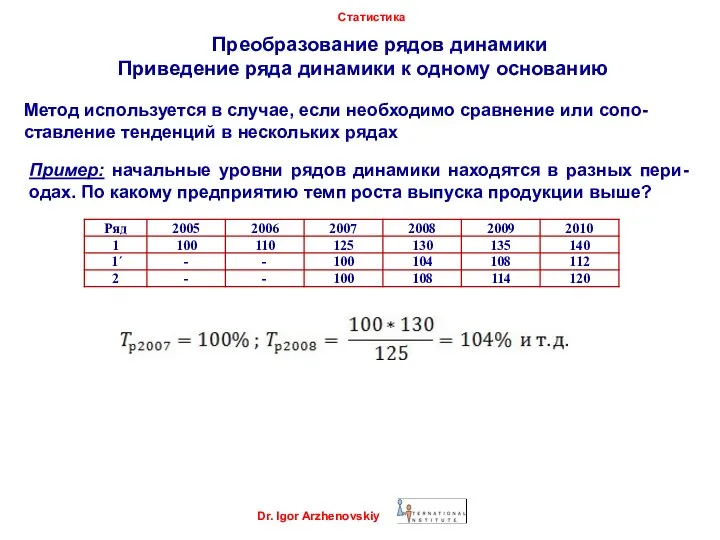
Dr. Igor Arzhenovskiy
Статистика
Преобразование рядов динамики
Приведение ряда динамики к одному основанию
Метод используется в случае, если необходимо сравнение или сопо-ставление тенденций в нескольких рядах
Пример: начальные уровни рядов динамики находятся в разных пери-одах. По какому предприятию темп роста выпуска продукции выше?

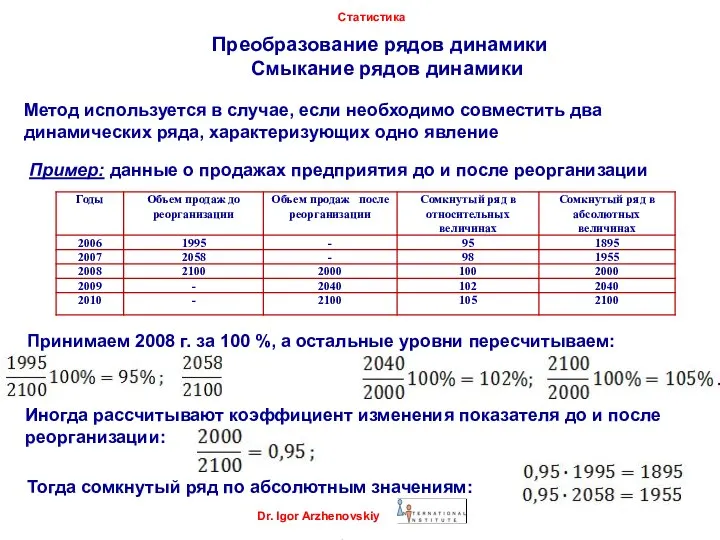
Dr. Igor Arzhenovskiy
Статистика
Преобразование рядов динамики
Смыкание рядов динамики
Метод используется в случае, если необходимо совместить два динамических ряда, характеризующих одно явление
Пример: данные о продажах предприятия до и после реорганизации
Принимаем 2008 г. за 100 %, а остальные уровни пересчитываем:
Иногда рассчитывают коэффициент изменения показателя до и после
реорганизации:
Теперь можно составить сомкнутый ряд по абсолютным значениям:
Тогда сомкнутый ряд по абсолютным значениям:

Dr. Igor Arzhenovskiy
Статистика
Преобразование рядов динамики
Интерполяция и экстраполяция
Интерполяция – нахождение уровней внутри динамического ряда
Экстраполяция – нахождение уровней за пределами динамического ряда
Пример: (см. выше)
Точность прогноза с ростом горизонта прогнозирования уменьшается, поэтому не рекомендуется делать прогнозы на срок, более чем на 1/3 превышающий длительность периода, по которому строился тренд.
Другие причины прогнозных ошибок могут быть:
- неправильный подбор факторного признака;
- неточный расчёт параметров модели (например, в случае линейной зависимости – коэффициентов a и b);
- несоблюдение допущений модели, например, в отношении остаточной компоненты R(t).
- выбор для исследования неподходящего периода времени.

Dr. Igor Arzhenovskiy
Статистика
Определение и устранение сезонных колебаний
1. Если тренд не известен
- Определяем среднемесячные
итоговые величины
- Рассчитываем относительные
показатели
- Определяем сезонную
компоненту
- Исключаем влияние сезонной
компоненты
2. Если тренд известен
- Рассчитываем тренд
- Определяем вид связи
компонент и рассчитываем
сезонные значения
- Определяем сезонную
компоненту
- Исключаем влияние сезонной
компоненты

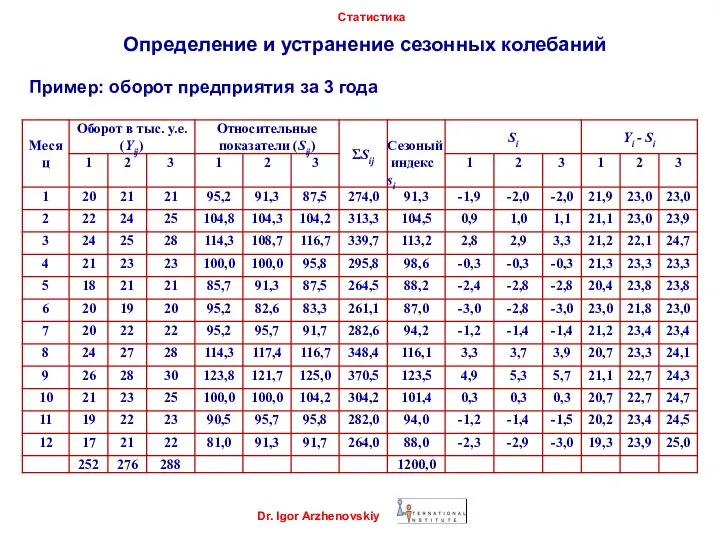
Dr. Igor Arzhenovskiy
Статистика
Определение и устранение сезонных колебаний
Пример: оборот предприятия за 3 года

Dr. Igor Arzhenovskiy
Статистика
Определение и устранение сезонных колебаний
1) Определяем среднемесячные оборот по годам
1 год – 252/12=21
2 год – 276/12=23
3 год – 288/12=24
2) Рассчитываем относительные показатели (Sij):
Январь 1-го года:
Результат (95,2%) показывает, что оборот в этот период был на 4,8% ниже
среднемесячного уровня.
Январь 2-го года:
и т.д.

Dr. Igor Arzhenovskiy
Статистика
Определение и устранение сезонных колебаний
3) Рассчитанные величины для одноименных месяцев складываются и вычисляется их средняя (сезонный индекс si)
Он означает сезонные колебания в январе на 8,7 % ниже нормального
годового значения
4) Определяем сезонную компоненту
Исключаем влияние сезонной компоненты:
Т.е. если бы в этот период не было бы сезонных колебаний, то оборот предприятия составил бы 21,9 .

Тема 10. Выборка
1. Понятие выборки
2. Способы отбора
3. Ошибки выборки
4. Доверительные интервалы. Распространение результатов выборки на всю совокупность
5. Необходимая численность выборки
6. Практика применения выборки
Dr. Igor Arzhenovskiy
Статистика

Понятие выборки
Выборка – это один из видов несплошного наблюдения, когда о целом судят по его части.
Условия проведения выборки:
1) требуемая точность устанавливается самостоятельно
2) выборка должна давать значительное сокращение ресурсов и времени по сравнению со сплошным наблюдением
Этапы выборочного наблюдения:
- формулировка целей и задач исследования, обоснование выборки
- уточнение границ генеральной совокупности
- определение объёма выборки
- проведение выборки
- расчет выборочных характеристик и ошибок
- распространение результатов выборки на генеральную совокупность
- анализ, оценка и интерпретация полученных результатов
Dr. Igor Arzhenovskiy
Статистика
N, n, , , w, p, σ², s²
Условные обозначения:

Cпособы отбора
Dr. Igor Arzhenovskiy
Статистика
1) Собственно случайный отбор - это отбор по жребию, по таблице случайных чисел (в настоящее время генерируется компьютером).
Бывает повторным (отобранная единица совокупности может снова попасть в выборку) и бесповторным (отобранная единица совокупности вновь в выборку не возвращается).
Пример повторного обора: измерение плотности пассажиропотока на транспорте
Пример бесповторного отбора: лотерея «Спортлото»
2) Механический отбор - это отбор из списков. На всю генеральную совокупность составляется общий список и далее из него через равный интервал отбирают нужное количество единиц.
Размер интервала равен 1/долю выборки. Так, при 2 %-ной выборке интервал будет равен 1/0,02 = 50 ед.
Общий список составляется двумя способами: единицы совокупности располагаются в случайном порядке (отбор можно начинать с любой единицы) или в определенном порядке ( отбор начинают с середины первого интервала)
Примеры: табельные номера работников предприятия (первый вариант), алфавитный список студентов потока (второй вариант)

Способы отбора
Dr. Igor Arzhenovskiy
Статистика
3) Типический отбор - генеральная совокупность разбивается на типические группы, которые должны как можно сильнее отличаться друг от друга и быть однородными внутри. Затем из каждой типической группы первыми двумя способами отбирают единицы в выборочную совокупность.
Пример: обследуются предприятия различных форм собственности. Формы собственности представляют различные типические группы
4) Серийный отбор - генеральная совокупность разбивается на серии. Серии должны как можно менее отличаться друг от друга и быть разнородными внутри. Обследуется часть серий, зато внутри серии – как правило, все единицы. Отбор из серий в выборку также осуществляется первыми двумя способами.
Пример: обследование одного ящика пива из партии.
Другие способы отбора: в прикладных исследованиях применяются такие неслучайные способы отбора, как квотный, «удобная выборка» (Convenience sample), экспертный и другие

Ошибки выборки
Dr. Igor Arzhenovskiy
Статистика
где Δ – предельная ошибка выборки
Выборка характеризуется прежде всего ошибками представительства или репрезентативности. Их суть: отклонения выборочных значений от генеральных:
1) Случайный отбор
- повторный случайный отбор:
где μ средняя (стандартная) ошибка выборки
t – кратность средней ошибки выборки
n – объем выборки
Пример1: на предприятии оценивается средний возраст работников. Найти предельную ошибку выборки с вероятностью 0,997, если стандартное отклонение σ = 4, а объём выборки n = 150 чел.
Тогда:

Ошибки выборки
Dr. Igor Arzhenovskiy
Статистика
Случайный отбор
- повторный случайный отбор:
Пример 2.: из стада в 10 тыс. коров обследовано 100 коров. Половина из обследованных признана породистой. Определить долю породистых коров во всем стаде.
w = 0,5
При t = 1,96 (вероятность 95%): Δ = 1,96 = 0,098
- бесповторный случайный отбор:
Доля породистых коров во всем стаде: p = w ± Δ= 0,5 ± 0,098
Т.е. с вероятностью 95% можно утверждать, что во всем стаде породистых коров 50 ± 9,8 %
2) Механический отбор.
Используются те же формулы, хотя фактически ошибки меньше.
Т.е. ошибки завышаются, но повышается надёжность оценок.

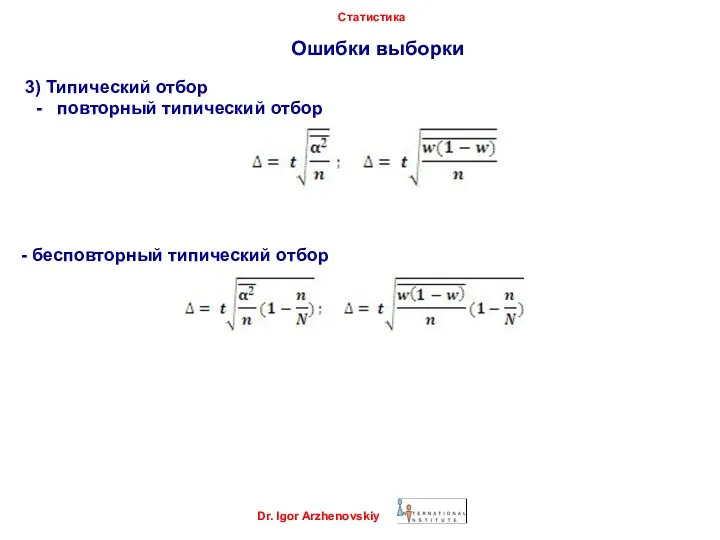
Ошибки выборки
Dr. Igor Arzhenovskiy
Статистика
3) Типический отбор
- повторный типический отбор
- бесповторный типический отбор

Ошибки выборки
Dr. Igor Arzhenovskiy
Статистика
4) Серийный отбор
- повторный серийный отбор
- бесповторный серийный отбор
Если внутри серий обследуются не все единицы, формулы усложняются:
повторный серийный отбор бесповторный серийный отбор
где m – число отобранных в сериях единиц

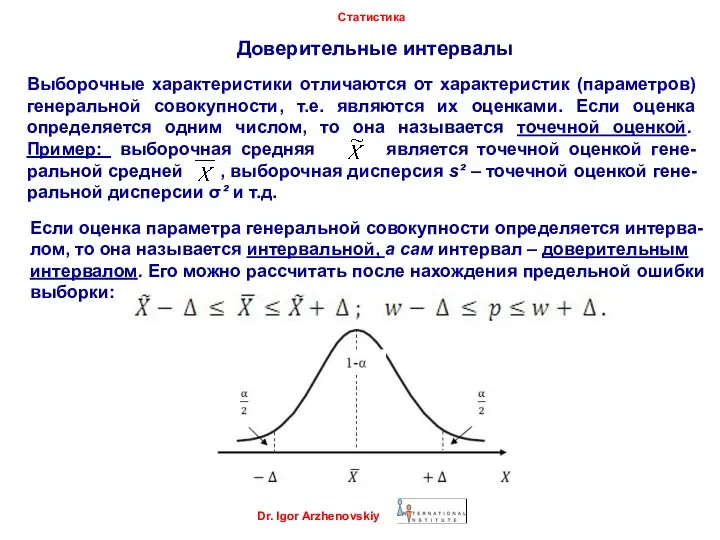
Доверительные интервалы
Dr. Igor Arzhenovskiy
Статистика
Выборочные характеристики отличаются от характеристик (параметров) генеральной совокупности, т.е. являются их оценками. Если оценка определяется одним числом, то она называется точечной оценкой. Пример: выборочная средняя является точечной оценкой гене-ральной средней , выборочная дисперсия s² – точечной оценкой гене-ральной дисперсии σ² и т.д.
Если оценка параметра генеральной совокупности определяется интерва-
лом, то она называется интервальной, а сам интервал – доверительным
интервалом. Его можно рассчитать после нахождения предельной ошибки
выборки:

Доверительные интервалы
Dr. Igor Arzhenovskiy
Статистика
Пример: при проверке изделий на наличие брака произведена случайная повторная выборка n = 1000 ед., при этом доля бракованных изделий составила w = 0,2 (20 %). Определить с вероятностью 99,7 % (t = 3) доверительный интервал для доли брака в совокупности.
Относительная ошибка выборки
для средней: для доли:
причём в знаменателе можно подставить выборочные значения. Если
не превышает заранее установленного предельного значения, то выборка
репрезентативна и может распространяться на генеральную совокупность.

Распространение результатов выборки на всю совокупность
Dr. Igor Arzhenovskiy
Статистика
- Метод прямого пересчета заключается в умножении средней выборочной
на объем генеральной совокупности.
Пример: сколько бракованных изделий содержится в серии из 100 000 ед.?
С вероятностью 99,7 % число бракованных изделий будет лежать между:
0,1621 ∙ 100 000 и 0,2379 ∙ 100 000 ед., т.е. между 16210 и 23790 ед.
- Метод коэффициентов более точен. Используют следующую формулу:
Y1 = Y0 K,
где К – поправочный коэффициент
Пример: зарегистрированных торговых мест на рынке Y0 = 500,
выборочная проверка участка А рынка показала, что на 40 зарегистриро-
ванных приходится 10 неучтенных мест, т.е. поправочный коэффициент
К = 50 : 40 = 1,25
Тогда на всём рынке будет:
Y1 = Y0 K или Y1 = 500 · 1,25 = 625 мест.

Необходимая численность выборки
Dr. Igor Arzhenovskiy
Статистика
Объём выборки – это число единиц генеральной совокупности, которое мы должны обследовать, не превышая предельную ошибку Δ с вероятностью p.
Расчёта объёма выборки зависит от способа отбора:
1) Случайный отбор.
- повторный отбор:
- бесповторный отбор:
Пример: определить численность выборки, если
Δ2 = 0,01
N = 100
σ2 = 1
t = 2
Тогда n = = 80 ⇒ лучше провести сплошное обследование

Необходимая численность выборки
Dr. Igor Arzhenovskiy
Статистика
2) Механический отбор – используются формулы случайного отбора
- бесповторный отбор:
3) Типический отбор
- повторный отбор:
4) Серийный отбор
- повторный отбор:
- бесповторный отбор:

Практика применения выборки
Dr. Igor Arzhenovskiy
Статистика
Основные направления применения выборочного метода:
● маркетинговые исследования
● изучение общественного мнения
● обследование уровня цен и объемов продаж в регионах
● оценка качества продукции
● статистический контроль производства
● обработка материалов переписи населения и переписей вообще
Пример1: оценка генеральной доли. В ходе исследования по выведению на рынок нового лекарства А было установлено, что доля купивших ле-карство составила 2 %. Объём бесповторной случайной выборки равен 1000 чел. Объём генеральной совокупности оценивается в 25 000 чел.
Тогда величина стандартной ошибки выборки по доле составит:
Т.е. с вероятностью 95,4 % можно утверждать, что предельная ошибка выборки ≤ 0, 86 %. Доля купивших препарат А находится в интервале
1,14 ≤ p ≤ 2,86 .

Практика применения выборки
Dr. Igor Arzhenovskiy
Статистика
Пример 2: определение объёма выборки.
В ходе изучения конъюнктуры рынка необходимо с помощью выборки выявить среднюю цену на товар В. Разница между максимальной и минимальной ценой товара не может превышать 24 руб. Исходя из допущения нормального распределения цен на товар В в диапазон x ± 3σ включается 99,7 % всех вариантов значений цены, т.е. 24 ≈ 6σ. Предельная ошибка повторной случайной выборки установлена на уровне 1 руб. Доверительная вероятность принята равной 95,4 %.
Тогда искомый объём выборки составит:
Для сравнения: если бы мы хотели узнать среднюю цену на товар В с предельной ошибкой не более 50 коп., то, при прочих равных условиях, нам бы понадобилась выборка объёмом:

Тема 11. Статистическая проверка гипотез
1. Основные понятия и определения
2. Ошибки при проверке гипотез
3. Статистические критерии. Критическая область. Область принятия гипотезы
4. Общая схема проверки гипотез
5. Параметрические и непараметрические тесты
- критерии согласия
- Z-критерий
- T-критерий
- F-критерий
Dr. Igor Arzhenovskiy
Статистика

Основные понятия и определения
Dr. Igor Arzhenovskiy
Статистика
Статистическая гипотеза – это предположение о свойствах случайных величин или событий, которое мы хотим проверить по имеющимся данным.
Различают два вида статистических гипотез:
гипотезы о неизвестных параметрах генеральной совокупности. Они
проверяются параметрическими тестами.
Пример: дисперсии 2-х нормальных совокупностей равны между собой
2) гипотезы о неизвестной форме распределения генеральной совокуп-
ности. Они проверяются непараметрическими тестами).
Пример: генеральная совокупность распределена по закону Пуассона
Исходное утверждение, которое берут за основу, - нулевая гипотеза Н0
Другое проверяемое предположение, которое противоречит исходному, - альтернативная гипотеза Н1.
Пример: производитель молока утверждает, что его средняя жирность равна 3,2%. Представитель торговой сети не согласен с данным утверждением. Тогда:
Н0 : = 3,2 %
Н1 : ≠ 3,2 % или Н1 : ≥ 3,2 %

Ошибки при проверке гипотез
Dr. Igor Arzhenovskiy
Статистика
Ошибки, допускаемые при проверке гипотез, делятся на два типа:
отклонение гипотезы Н0, когда она верна, — ошибка первого рода;
принятие гипотезы Н0, когда в действительности верна какая-то другая гипотеза, — ошибка второго рода.
Вероятность ошибки первого рода обозначается α и называется уровнем значимости, по которому проверяется справедливость гипотезы Н0.
Вероятность ошибки второго рода обозначается β. Ее величина зависит от альтернативной гипотезы Н1 .
Уровень значимости α задается исследователем самостоятельно, до про-верки гипотезы. Обычно считают достаточным α = 0,05, иногда α = 0,01, редко α = 0,001.

Статистические критерии
Dr. Igor Arzhenovskiy
Статистика
Для проверки выдвинутых нулевых гипотез используют случайную величину К, которую называют статистическим критерием.
Статистические критерии подразделяются на три типа:
1. Критерии значимости, которые служат для проверки гипотез о парамет-
рах распределений генеральной совокупности (чаще всего нормально-
го распределения). Эти критерии называются параметрическими.
Пример: Z-критерий в случае стандартного нормального распределения,
F-критерий в случае распределения Фишера, T-критерий в случае
распределения Стьюдента.
2. Критерии, которые для проверки гипотез не используют предположений
о распределении генеральной совокупности. Эти критерии не требуют
знания параметров распределений, поэтому называются непараметри-
ческими. Пример: D-критерий Колмогорова-Смирнова.
3. Критерии согласия служат для проверки гипотез о согласии распреде-
ления генеральной совокупности, из которой получена выборка, с ранее
принятой теоретической моделью (чаще всего нормальным распределе-
нием). Пример: критерий согласия χ2.

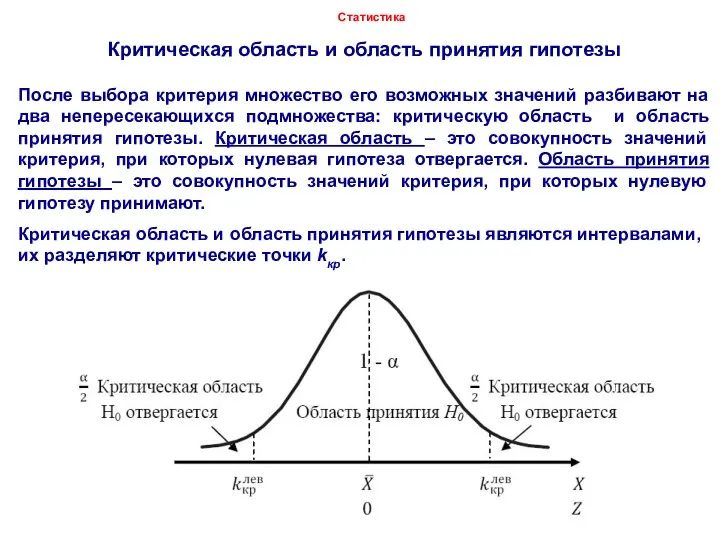
Критическая область и область принятия гипотезы
Dr. Igor Arzhenovskiy
Статистика
После выбора критерия множество его возможных значений разбивают на два непересекающихся подмножества: критическую область и область принятия гипотезы. Критическая область – это совокупность значений критерия, при которых нулевая гипотеза отвергается. Область принятия гипотезы – это совокупность значений критерия, при которых нулевую гипотезу принимают.
Критическая область и область принятия гипотезы являются интервалами, их разделяют критические точки kкр.

Общая схема проверки гипотез
Dr. Igor Arzhenovskiy
Статистика
Формулируются нулевая и альтернативная гипотезы Н0 и Н1.
Выбирается уровень значимости α
2. Выбирается подходящий статистический критерий и определяется
форма распределения, используемая в тесте
Определяется критическая область и область принятия гипотезы
4. Вычисляется наблюдаемое и критическое (граничное) значения
критерия при уровне значимости α
5. Найденное значение Kнабл критерия сравнивается с Ккр .
По результатам сравнения делается вывод: принять гипотезу или
отвергнуть

Общая схема проверки гипотез: пример
Dr. Igor Arzhenovskiy
Статистика
Оценить значимость коэффициента корреляции r = 0,89 при числе выборочных наблюдений n = 6.
1. Нулевая гипотеза: коэффициент корреляции r равен нулю, т.е. связь
между факторным признаком x и результативным признаком y
отсутствует.
Н0 : r = 0
Н1 : r ≠ 0
Примем уровень значимости α = 0,05.
2. Так как выборка малая, распределение r будет отличаться от нормаль-
ного, подходящим статистическим критерием будет выступать
t-критерий Стьюдента с n - 2 степенями свободы.
3. Критические (табличные) значение t-критерия по таблице распределения Стьюдента при n - 2 = 6 – 2 = 4 равны:
tтабл = ± 2,78

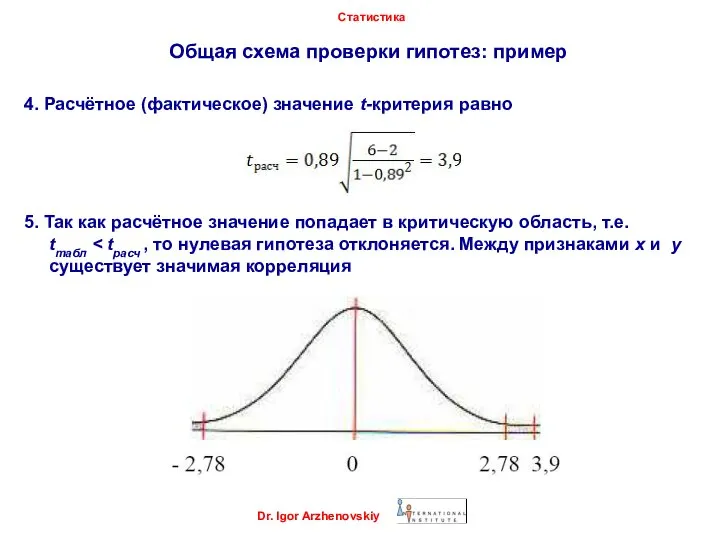
Общая схема проверки гипотез: пример
Dr. Igor Arzhenovskiy
Статистика
4. Расчётное (фактическое) значение t-критерия равно
5. Так как расчётное значение попадает в критическую область, т.е.
tтабл < tрасч , то нулевая гипотеза отклоняется. Между признаками x и y
существует значимая корреляция

Критерий согласия χ2
Dr. Igor Arzhenovskiy
Статистика
Применяется для проверки предположения о нормальном распределении генеральной совокупности.
Н0: fo (x) = fe (x)
Н1: fo(x) ≠ fe (x)
где fo - эмпирические (фактические)частоты интервалов группировки
fe – теоретические (ожидаемые) частоты, рассчитываются по формулам нормального
распределения
Формулируется гипотеза, выбирается уровень значимости α
2. Получается выборка объема n ≥ 30 независимых наблюдений и предста-
вляется эмпирическое распределение в виде интервального вариацион-
ного ряда
3. Рассчитываются выборочные характеристики и s.
4. Вычисляются значения теоретических частот fe попадания в i-й интер-
вал группировки
fei = pi n
где pi = F(zi) – F(zo),
F(z) - функции Лапласа,
z - стандартная оценка

Критерий согласия χ2
Dr. Igor Arzhenovskiy
Статистика
6. Из таблиц распределения χ2 находится критическое значение χ2табл
критерия для уровня значимости α и числа степеней свободы n - 3.
7. Вывод: если χ2расч ≥ χ2табл , то эмпирическое распределение не соответствует нормальному распределению при уровне значимости α, в противном случае нет оснований отрицать это соответствие.
Пример: проверить нормальный характер распределения объема продаж в супермаркете при уровне значимости α = 0,05 и следующих данных:

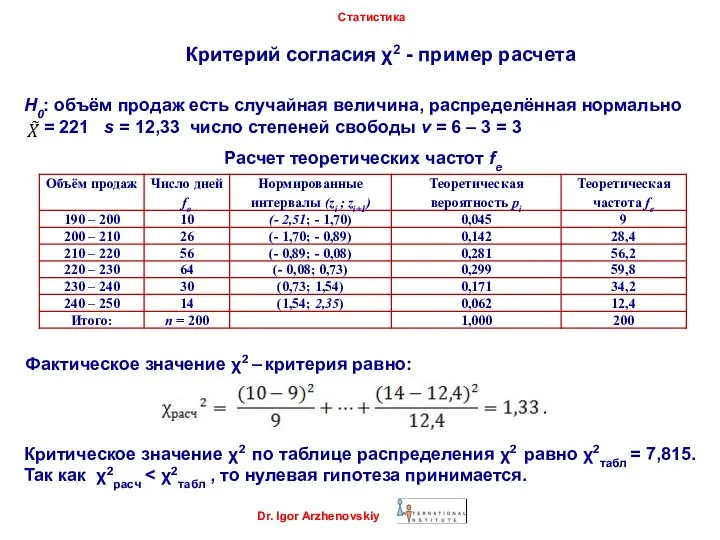
Критерий согласия χ2 - пример расчета
Dr. Igor Arzhenovskiy
Статистика
Н0: объём продаж есть случайная величина, распределённая нормально
= 221 s = 12,33 число степеней свободы v = 6 – 3 = 3
Расчет теоретических частот fe
Фактическое значение χ2 – критерия равно:
Критическое значение χ2 по таблице распределения χ2 равно χ2табл = 7,815. Так как χ2расч < χ2табл , то нулевая гипотеза принимается.

Z - критерий
Dr. Igor Arzhenovskiy
Статистика
Применяется для оценки значимости отклонений параметров генеральной совокупности от выборки, например, выборочной средней от генеральной средней, при известной генеральной дисперсии σ2
Н0: =
Н1: ≠
Принимаем предположение о нормальности, формулируем гипотезы
Н0 и H1 задаем уровень значимости α
Получаем выборку объема n
Вычисляем среднюю арифметическую выборочную
4. Определяем значение Z - критерия по формуле:
Уровень значимости: α.

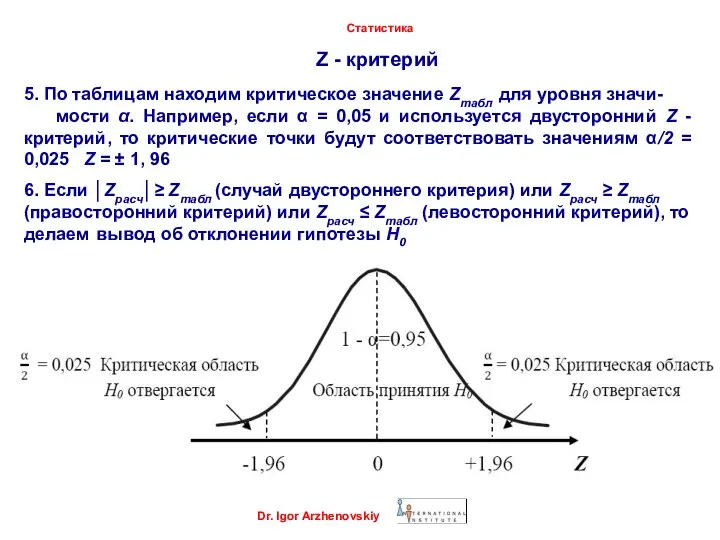
Z - критерий
Dr. Igor Arzhenovskiy
Статистика
5. По таблицам находим критическое значение Zтабл для уровня значи-
мости α. Например, если α = 0,05 и используется двусторонний Z - критерий, то критические точки будут соответствовать значениям α/2 = 0,025 Z = ± 1, 96
6. Если │Zрасч│≥ Zтабл (случай двустороннего критерия) или Zрасч ≥ Zтабл (правосторонний критерий) или Zрасч ≤ Zтабл (левосторонний критерий), то делаем вывод об отклонении гипотезы Н0

Z – критерий – пример расчета
Dr. Igor Arzhenovskiy
Статистика
Вы являетесь менеджером на кондитерской фабрике, которая выпускает набор конфет «Ассорти»» весом = 368 г. Выборка объёмом n = 25 дала средний вес набора = 372,5 г. Является ли различие существенным и необходима ли переналадка фабричного оборудования, если σ = 15? Распределение генеральной совокупности близко к нормальному.
Н0: = 368 г.
Н1: ≠ 368 г.
α = 0,05
Zтабл= ± 1,96
Так как │Zрасч│< Zтабл , то нулевая гипотеза не отклоняется. Мер по пере-наладке оборудования на фабрике предпринимать не нужно.

Dr. Igor Arzhenovskiy
Статистика
Т - критерий
Применяется для оценки значимости отклонений параметров генеральной совокупности от выборки при неизвестной генеральной дисперсии σ2. Вместо нее используется выборочная дисперсия s2
Используют t – распределению Стьюдента с v = n – 1 степенями свободы
Пример расчета: термопластоавтомат изготавливает пластмассовую крышку средней толщиной = 0,25 см. Выборка объёмом n = 10 дала выборочную среднюю = 0,253 см. при выборочном стандартном откло- нении s = 0,003 см. Нужно проверить предположение, что при уровне значимости α = 0,05 термопластоавтомат работает точно.
Н0: = 0,25 см.
Н1: ≠ 0,25 см.
α = 0,05
v = 10 – 1 = 9
Ттабл= ± 2,262
Так как │Трасч│> Ттабл , то Н0 отклоняется: нельзя утверждать, что термо-пластоавтомат работает точно

Dr. Igor Arzhenovskiy
Статистика
F-критерий
Применяется для сравнения двух выборочных дисперсий из нормальных
генеральных совокупностей
H0: σx2 = σy2
H1: σx2 ≠ σy2 (двусторонний критерий) или H1: σ12 > σ22 2 (односторонний
критерий)
Уровень значимости задается α
1. Принимаем предположение о нормальном распределении генеральных
совокупностей, формулируем гипотезу и альтернативу, назначаем уро-
вень значимости α
2. Получаем две независимые выборки из совокупностей X и Y объемом
nх и nу соответственно
3. Рассчитываем значения выборочных дисперсий Sx2 и Sy2. Большая из
дисперсий S12, меньшая – S22
4. Вычисляем значение F-критерия
5. Сравниваем Fрасч с Fтабл при заданной α и v1 = n1 – 1 и v2 = n2 – 1.
6. Если Fрасч ≥ Fтабл , то дисперсии различаются значимо.