Квадратные неравенства (8 класс)

Квадратные неравенства
Определение: Квадратным называется
неравенство, левая часть которого −
квадратный трёхчлен, а правая часть
равна нулю:
ах²+bх+с>0 ах²+bх+с≥0
ах²+bх+с<0 ах²+bх+с≤0

Являются ли следующие неравенства квадратными?
А) 4у² - 5у +7 > 0 Б) 2х - 4 > 0
В) 4х² - 2х ≥ 0
Г) 3у – 5у² + 7 < 0
Д) 4 – 6х + 5х² ≤ 0
Е) 5у⁴ +3у - 6 < 0

Основные способы решения квадратных неравенств:
Метод интервалов
Графический метод

Запомним:
Чтобы решить квадратное неравенство
ах²+вх+с >0 методом интервалов надо:
1) Найти корни соответствующего
квадратного уравнения ах²+вх+с = 0;
2) Корни уравнения нанести на числовую ось;
3) Разделить числовую ось на интервалы;
3) Определить знаки функции в каждом из интервалов;
4) Выбрать подходящие интервалы и
записать ответ.

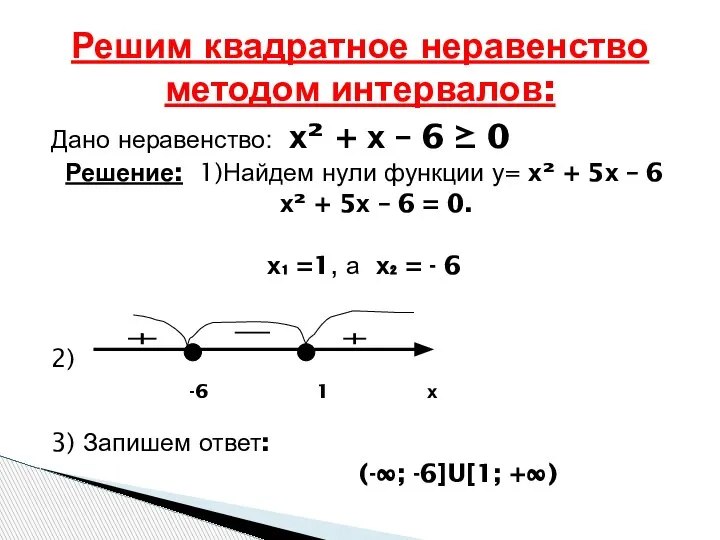
Решим квадратное неравенство методом интервалов:
Дано неравенство: х² + х – 6 ≥ 0
Решение: 1)Найдем нули функции у= х² + 5х – 6
х² + 5х – 6 = 0.
х₁ =1, а х₂ = - 6
2)
-6 1 х
3) Запишем ответ:
(-∞; -6]U[1; +∞)
+
+
-