Л 5 Функция одной переменной

Рассмотрим два множества X и Y с элементами, соответственно, x и y.
Определение 1. Если каждому элементу х из множества Х по некоторому правилу поставлен в соответствие единственный элемент y из множества Y, то говорят, что задана функция у=f(x), где х – аргумент (независимая переменная), у – значение функции (зависимая переменная), буква f обозначает правило, по которому получается значение у, отвечающее заданному х.
В1. Функция, способы задания функции

Если Х и Y – числовые множества, то отображение множества Х на множество Y называют числовой функцией.
Определение 2. Совокупность значений независимой переменной x, для которых определяются значения функции y, называется областью определения функции (или областью существования функции) и обозначается D.

Определение 3. Совокупность значений y, соответствующих всем значениям х∈D, называется областью изменения (значений) функции и обозначается Е.
Пример функции. Площадь S круга, есть функция его радиуса r, выражаемая формулой S = πr2 S = S(r).

Определение 4. Множество тех значений аргумента, при которых закон соответствия f имеет смысл, то есть функция имеет определенное, конечное значение, называется естественной областью определения функции.
Пример 1. Записать области определения функций и y = x + 1.
Решение.

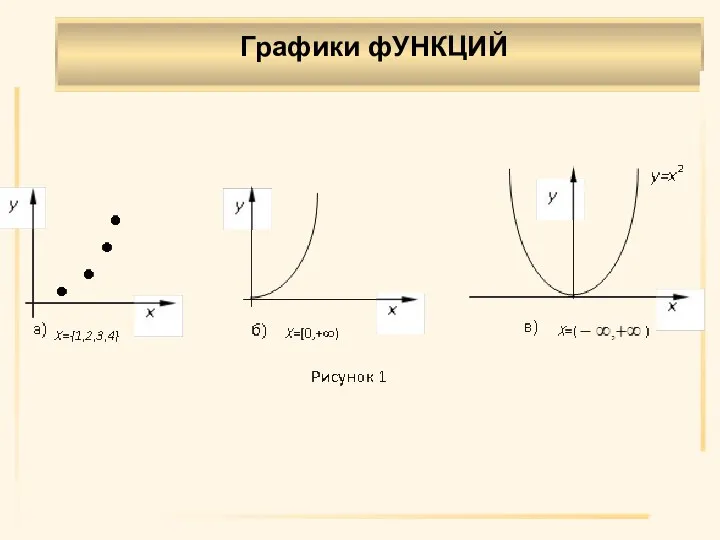
Пример 2. Построить графики функций, если известны области определения.
y = x2, X={1,2,3,4},
y = x2, X=[0, ) ,
y = x2, X= .
Это разные функции, так как области определения различны.
Пример 2.

Графики фУНКЦИЙ

Функция может быть задана различными способами:
- аналитически – в виде формулы (явно, неявно, параметрически),
- табличным способом,
- графически,
- с помощью словесной формулировки,
- программно.
СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ

В математике функция может быть задана словесно. Такова, например, функция Дирихле, которая определяется следующим образом:
D(x)=
4. Словесный (описательный) способ

Определение 4. Функция f(х) называется четной (нечетной), если она определена на множестве, симметричном относительно нулевой точки и обладает на нем свойством
f(–x) = f(x) ( f(–x) = – f(x) ).
2. Основные характеристики функции.

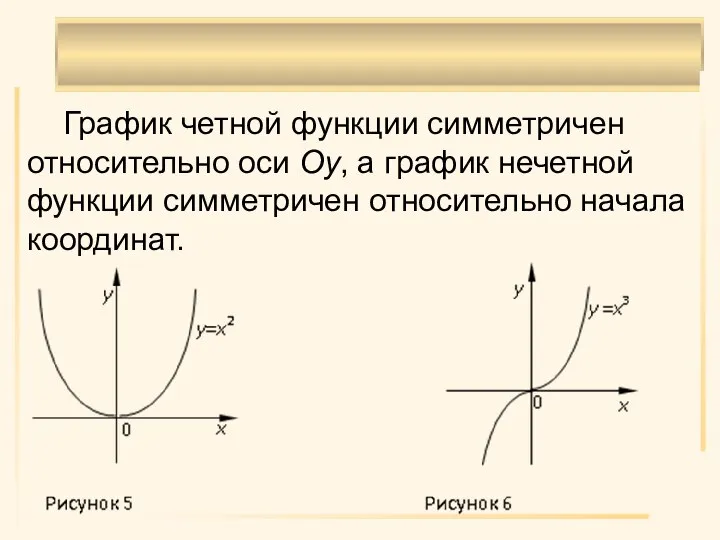
График четной функции симметричен относительно оси Oу, а график нечетной функции симметричен относительно начала координат.

Определение 5. Функция f(х), определенная на всей вещественной оси, называется периодической с периодом
Т > 0, если
f(x) = f(x+T) = f(x–T), для ∀х∈D.
Функции sinx, cosx, являются периодическими с периодом 2π, а функции tgx, ctgx имеют период π.

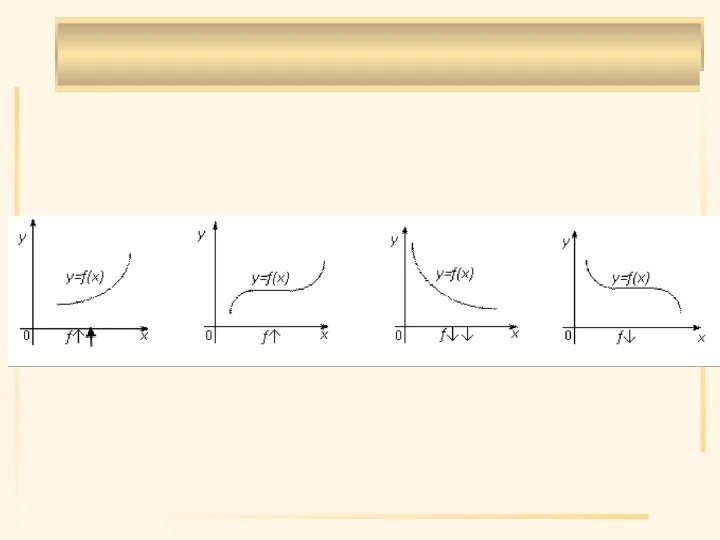
Определение 6. Функция y=f(x) называется возрастающей (неубывающей) на множестве X, если для любых двух значений x1 и x2 выполняется условие
f(x2)>f(x1) ( f(x2) f(x1) ) , если x1

Определение 7. Функция y=f(x) называется убывающей (невозрастающей) на множестве X, если выполняется условие
f(x2)
x1 и обозначают f↓↓(f↓).

Определение 8. Функция y=f(x) называется (строго) монотонной на множестве X, если она является (убывающей или возрастающей ) неубывающей или невозрастающей на множестве X.

Определение 9. Функция y=f(x) называется ограниченной на множестве X,

СЛОЖНЫЕ ФУНКЦИИ
В математике аналогом сложных систем, состоящих из элементов, выполняющих сравнительно простые действия, является композиция функций (сложная функция).
.
3. Сложные и обратные функции.

Понятие композиции функций
заключается в том, что вместо аргумента одной функции подставляется другая функция, зависящая от другого аргумента.
Например, у = sinx, z = lgy, то есть композиция функций z = lg(sinx).
Композиция функций

Определение 10. Пусть Y- множество значений функции y=f(x), заданной в области X. Если соответствует единственное значение такое, что f(x)=y, то определенная таким образом функция x=ϕ(y) называется обратной по отношению к функции y=f(x).
Обратные функции

Определение 11. Пусть y=f(z) и z=ϕ(x), определены соответственно на множествах Z и X. Если значениями функции z=ϕ(x) является множество Z, то данными функциями z=ϕ(x) и y=f(z) каждому значению х ставится в соответствие единственное значение y. Полученную таким образом функцию называют сложной функцией (композицией или суперпозицией функций) и записывают в виде y=f(ϕ(x)). Функция z=ϕ(x)- называется промежуточным аргументом.

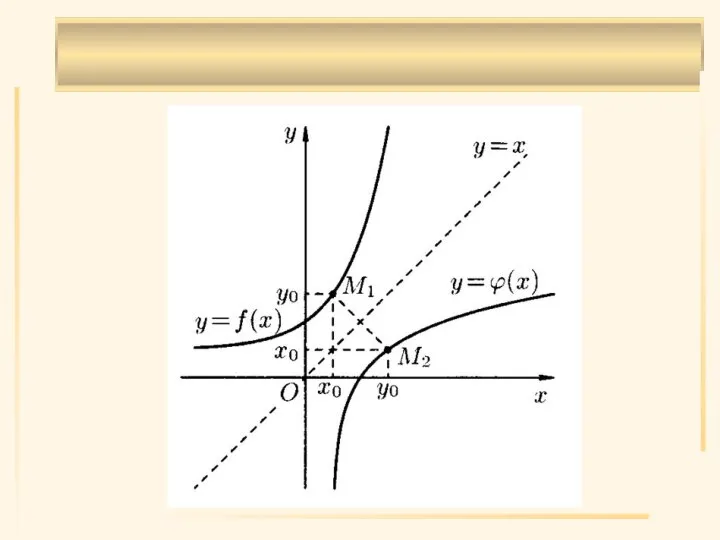
Определение 12. Пусть Y- множество значений функции y=f(x), заданной в области X. Если соответствует единственное значение такое, что f(x)=y, то определенная таким образом функция x=ϕ(y) называется обратной по отношению к функции y=f(x).

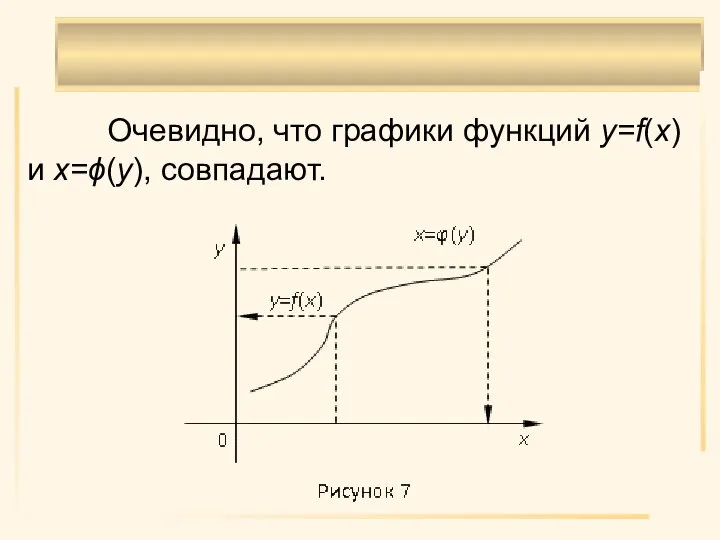
Очевидно, что графики функций y=f(x) и x=ϕ(y), совпадают.

Если функция y=f(x) строго монотонна на множестве Х, то в соответствующем промежутке Y значений этой функции существует однозначная обратная функция x=φ(у), также строго монотонная.
Теорема 1 (существование обратной функции).