Содержание
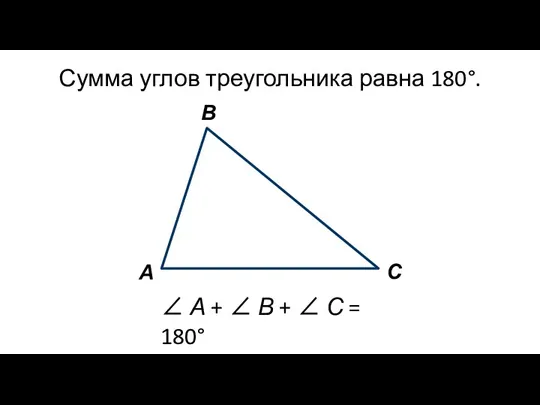
- 2. Сумма углов треугольника равна 180°. ∠ А + ∠ В + ∠ С = 180° А
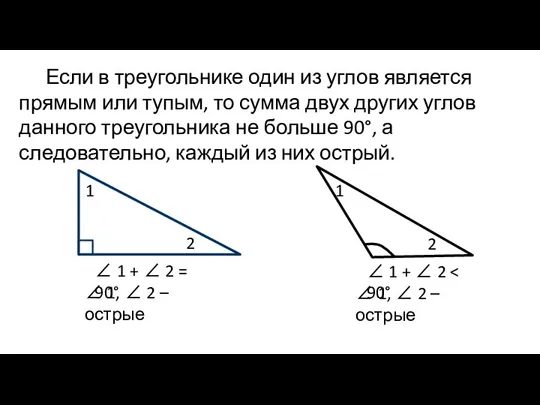
- 3. Если в треугольнике один из углов является прямым или тупым, то сумма двух других углов данного
- 4. Остроугольный треугольник – это треугольник, у которого все три угла острые. ∠ 1, ∠ 2, ∠
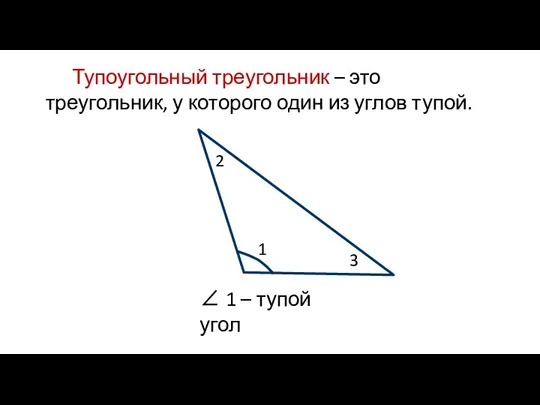
- 5. Тупоугольный треугольник – это треугольник, у которого один из углов тупой. ∠ 1 – тупой угол
- 6. Прямоугольный треугольник – это треугольник, у которого один из его углов является прямым. 1 3 2
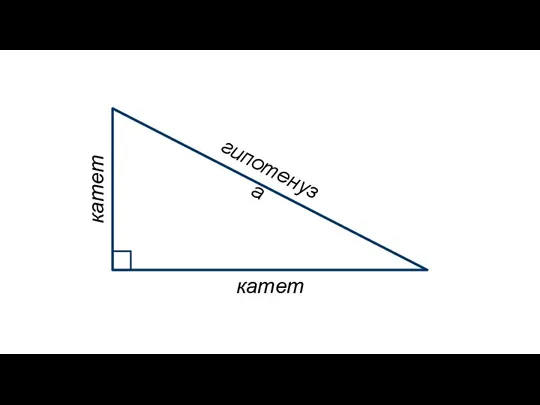
- 7. гипотенуза катет катет
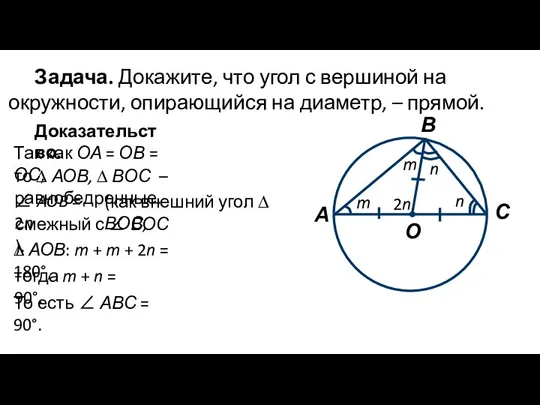
- 9. Задача. Докажите, что угол с вершиной на окружности, опирающийся на диаметр, – прямой. Доказательство. О С
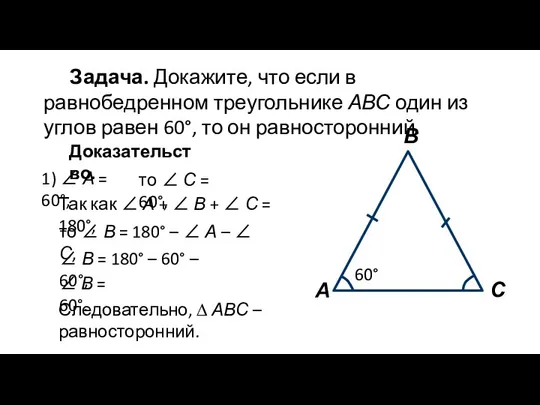
- 10. Задача. Докажите, что если в равнобедренном треугольнике АВС один из углов равен 60°, то он равносторонний.
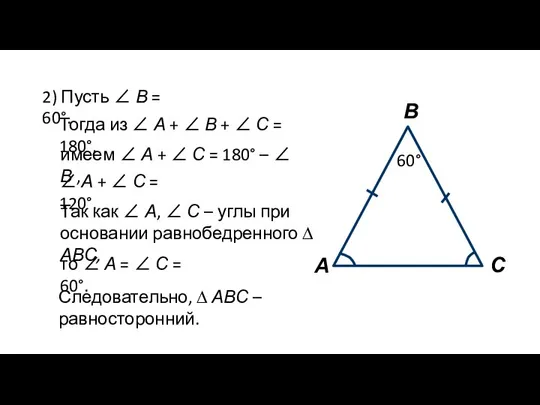
- 11. С В А 2) Пусть ∠ В = 60°. 60° Тогда из ∠ А + ∠
- 13. Скачать презентацию


 Подготовка к ГИА. Демоверсия 2013
Подготовка к ГИА. Демоверсия 2013 Мотивация … Статистика
Мотивация … Статистика Парная регрессия и корреляция
Парная регрессия и корреляция Простые и составные числа
Простые и составные числа Единицы измерения времени. Тренажёр
Единицы измерения времени. Тренажёр Дифференциальные уравнения
Дифференциальные уравнения Функция y=k/x, её график и свойства. 8 класс. Урок 2
Функция y=k/x, её график и свойства. 8 класс. Урок 2 Духовно-нравственное воспитание на уроках математики
Духовно-нравственное воспитание на уроках математики Особенности применения средств измерений в качестве эталонов единицы величины
Особенности применения средств измерений в качестве эталонов единицы величины Показательная функция
Показательная функция Теория расписаний. Минимизация приоритето-порождающих функций
Теория расписаний. Минимизация приоритето-порождающих функций Площадь треугольника
Площадь треугольника Признак перпендикулярности прямой и плоскости
Признак перпендикулярности прямой и плоскости Коррекция СУ
Коррекция СУ Римские цифры. 3 класс
Римские цифры. 3 класс Нулевая гипотеза
Нулевая гипотеза Стандартный вид числа в физике, астрономии и технике
Стандартный вид числа в физике, астрономии и технике Презентация на тему Математический диктант (4 класс)
Презентация на тему Математический диктант (4 класс)  Свойства четырёхугольников
Свойства четырёхугольников idkwhythatair
idkwhythatair Виды многоугольников
Виды многоугольников Числа от 1 до 5. Состав числа 5
Числа от 1 до 5. Состав числа 5 Письмо цифры 6
Письмо цифры 6 Сложение смешанных дробей
Сложение смешанных дробей Среднее арифметическое
Среднее арифметическое Стереометрия. Подготовка к ЕГЭ, задание В11
Стереометрия. Подготовка к ЕГЭ, задание В11 Математические методы в экономике. Лекция 8
Математические методы в экономике. Лекция 8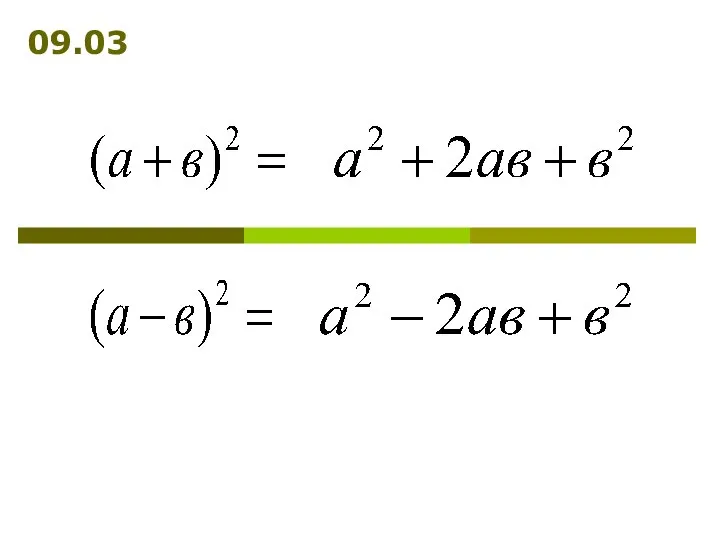 Преобразование многочленов с помощью формул сокращённого умножения
Преобразование многочленов с помощью формул сокращённого умножения