Содержание
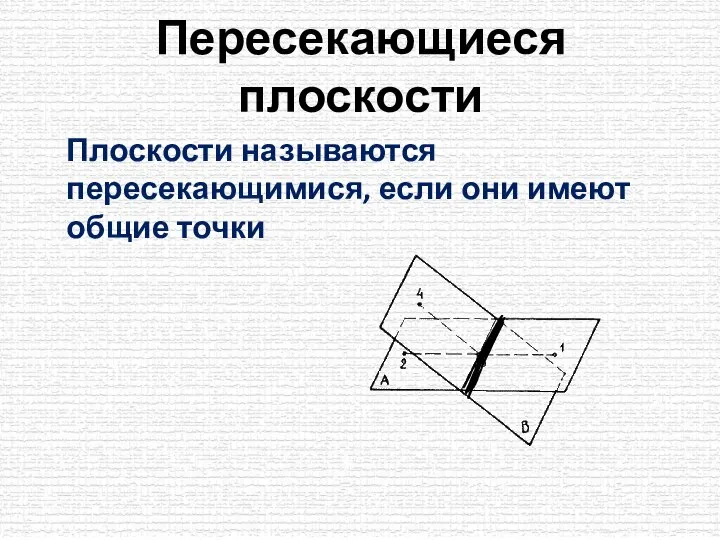
- 2. Пересекающиеся плоскости Плоскости называются пересекающимися, если они имеют общие точки
- 3. Параллельные плоскости Плоскости, не имеющие общих точек, называются параллельными
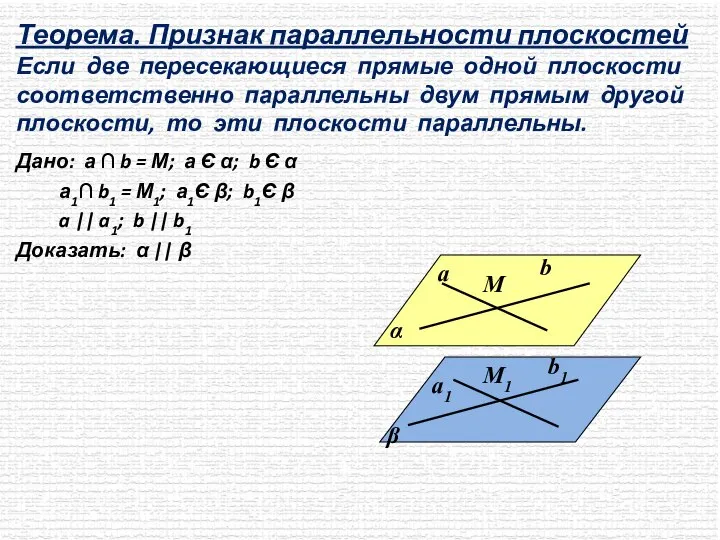
- 4. Теорема. Признак параллельности плоскостей Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости,
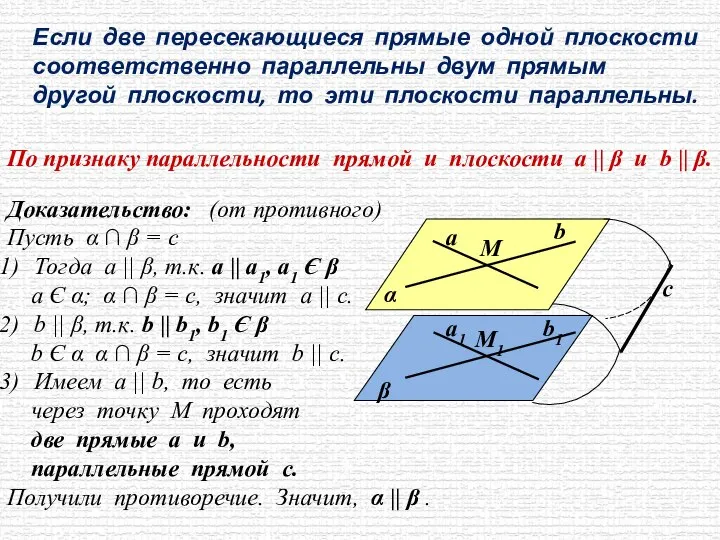
- 5. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
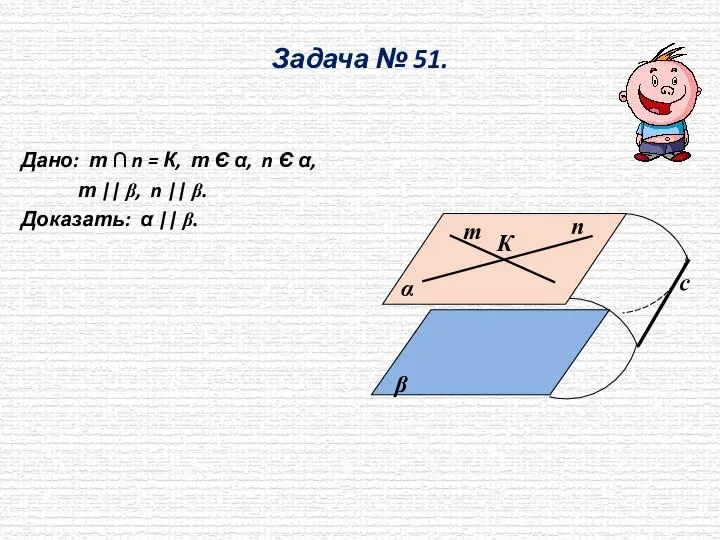
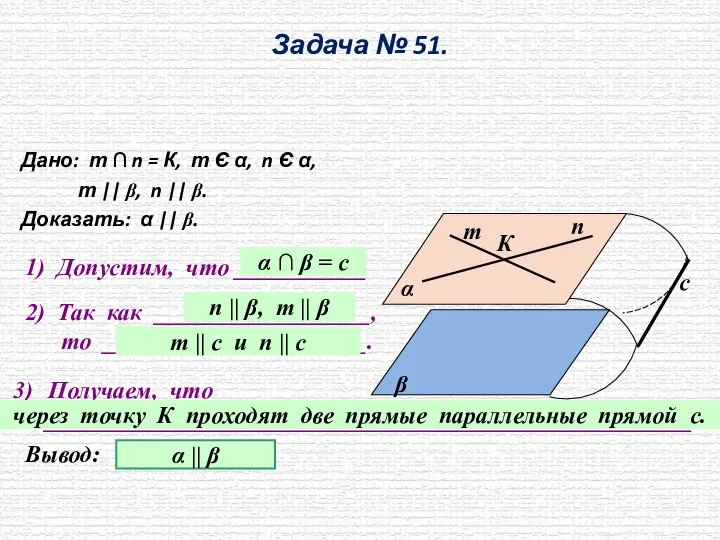
- 6. Задача № 51. Дано: т ∩ n = К, т Є α, n Є α, т
- 7. Задача № 51. Дано: т ∩ n = К, т Є α, n Є α, т
- 8. Проверка знаний Могут ли прямая и плоскость не иметь общих точек? Верно ли, что если две
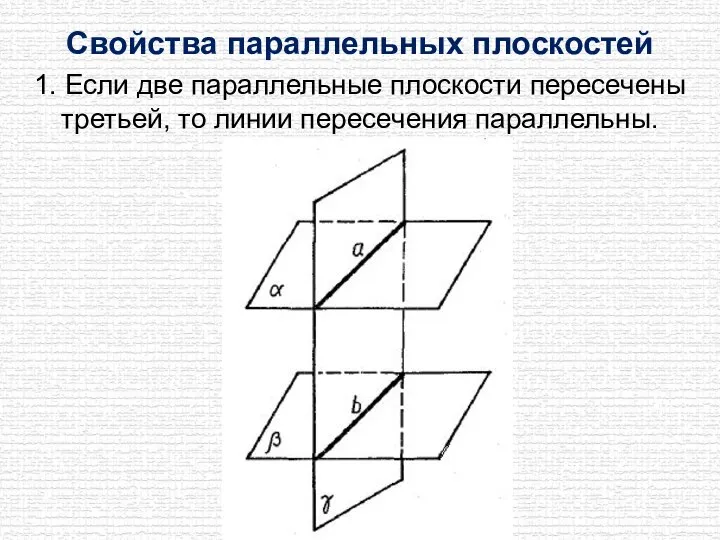
- 9. Свойства параллельных плоскостей 1. Если две параллельные плоскости пересечены третьей, то линии пересечения параллельны.
- 11. Скачать презентацию


 Свойства логарифмов. Решение примеров на свойства логарифмов и основное логарифмическое тождество
Свойства логарифмов. Решение примеров на свойства логарифмов и основное логарифмическое тождество Построение сечений многогранников
Построение сечений многогранников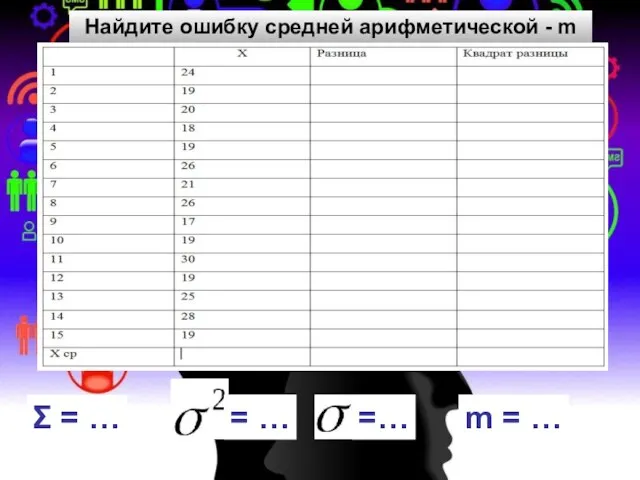 Средняя арифметическая
Средняя арифметическая Презентация на тему Формулы
Презентация на тему Формулы  Скалярное произведение векторов
Скалярное произведение векторов Презентация на тему Числовые промежутки
Презентация на тему Числовые промежутки  Сложение и вычитание вида +1 и -1
Сложение и вычитание вида +1 и -1 3.7. Непрерывность функции
3.7. Непрерывность функции По Щучьему велению на новый лад
По Щучьему велению на новый лад Средняя линия треугольника (8 класс)
Средняя линия треугольника (8 класс) Презентация на тему Возведение в степень произведения и степени (7 класс)
Презентация на тему Возведение в степень произведения и степени (7 класс)  Задачи с экономическим содержанием
Задачи с экономическим содержанием График функции
График функции Доказательство формулы сокращённого умножения (а b) (a b) a b другим способом
Доказательство формулы сокращённого умножения (а b) (a b) a b другим способом Применение производной к исследованию функции
Применение производной к исследованию функции Письменное умножение чисел, оканчивающихся нулями
Письменное умножение чисел, оканчивающихся нулями Линейное уравнение с двумя переменными
Линейное уравнение с двумя переменными Понятия много и один. Число и цифра 1
Понятия много и один. Число и цифра 1 История возникновения числа ПИ
История возникновения числа ПИ Формирование счетных навыков. Требования к счетной деятельности
Формирование счетных навыков. Требования к счетной деятельности Формулы приведения
Формулы приведения Калейдоскоп заданий ОГЭ. Математическая игра
Калейдоскоп заданий ОГЭ. Математическая игра Методика исследования понятия числа и его разрядной структуры, счетных операций
Методика исследования понятия числа и его разрядной структуры, счетных операций Решение дифференциальных уравнений с разделяющимися переменными
Решение дифференциальных уравнений с разделяющимися переменными Презентация на тему Великие математики и их открытия
Презентация на тему Великие математики и их открытия  Геометрический смысл производной f '(x₀) = tg α = к
Геометрический смысл производной f '(x₀) = tg α = к Окружность. Математика, ЕГЭ
Окружность. Математика, ЕГЭ ANX.ADJ.DSM.5
ANX.ADJ.DSM.5