Содержание
- 2. Треугольник
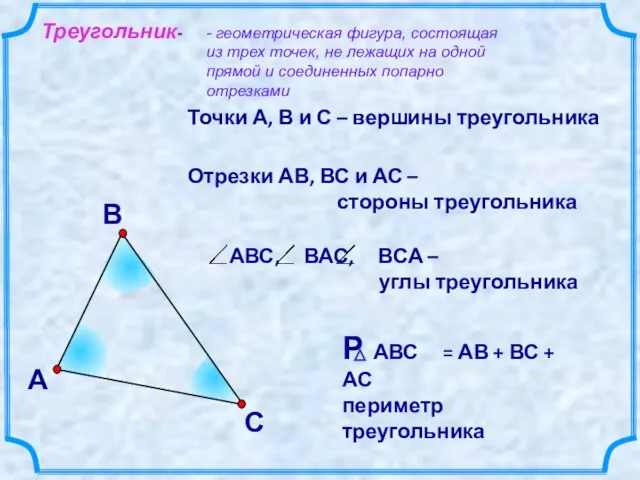
- 3. В А С Точки А, В и С – вершины треугольника Отрезки АВ, ВС и АС
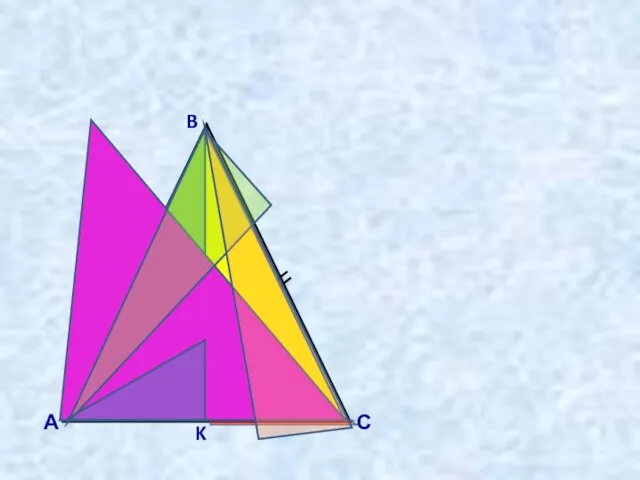
- 4. 1 B С О K А 2
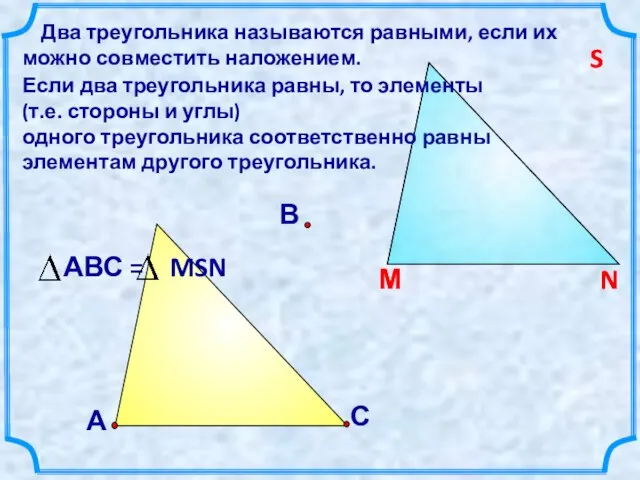
- 5. С В Два треугольника называются равными, если их можно совместить наложением. Если два треугольника равны, то
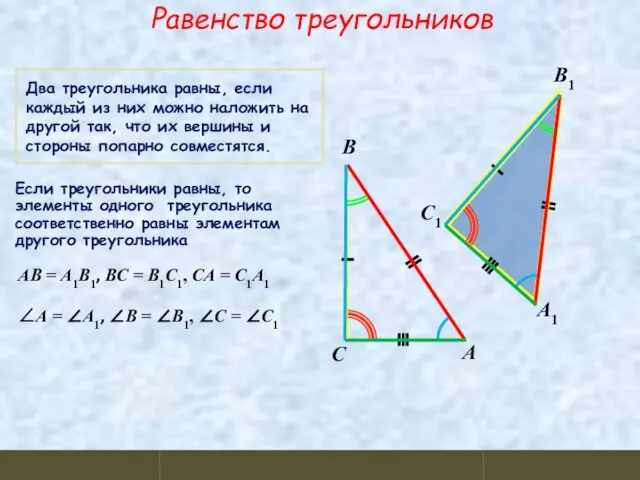
- 6. Равенство треугольников Два треугольника равны, если каждый из них можно наложить на другой так, что их
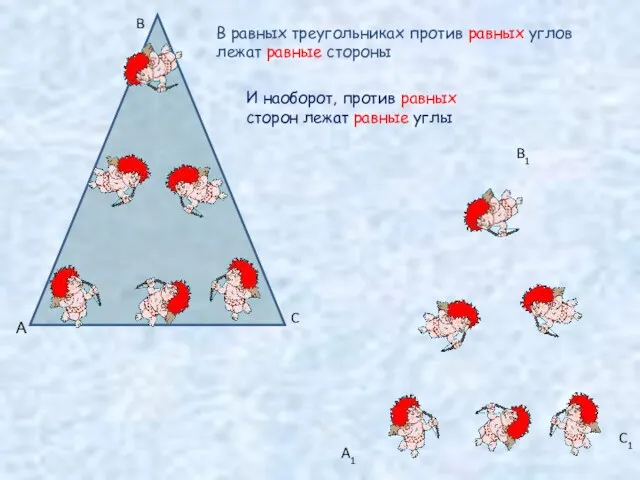
- 7. А B C A1 B1 C1 В равных треугольниках против равных углов лежат равные стороны И
- 8. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между
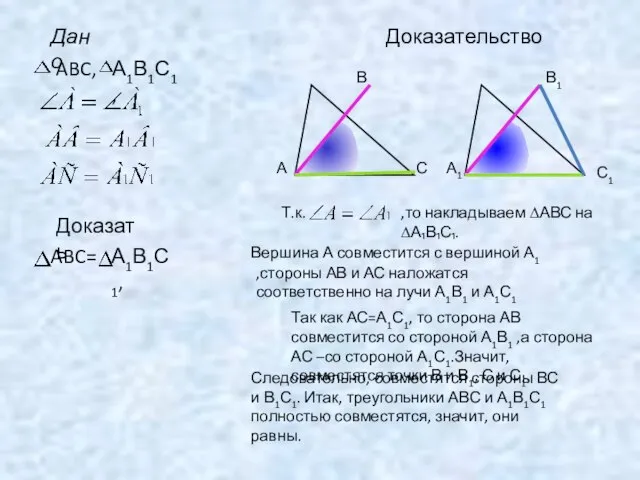
- 9. Доказать ABC= А1В1С1, Доказательство А В С А1 В1 С1 Т.к. ,то накладываем ∆АВС на ∆А₁В₁С₁.
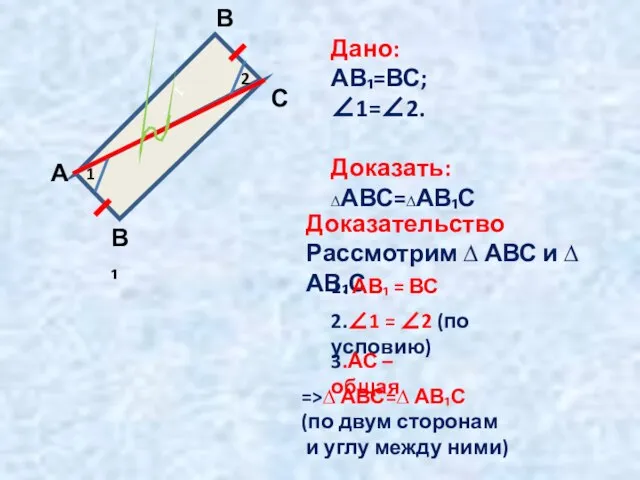
- 10. 1 1 2 А В С В₁ Дано: АВ₁=ВС; ∠1=∠2. Доказать: ∆АВС=∆АВ₁С Доказательство Рассмотрим ∆ АВС
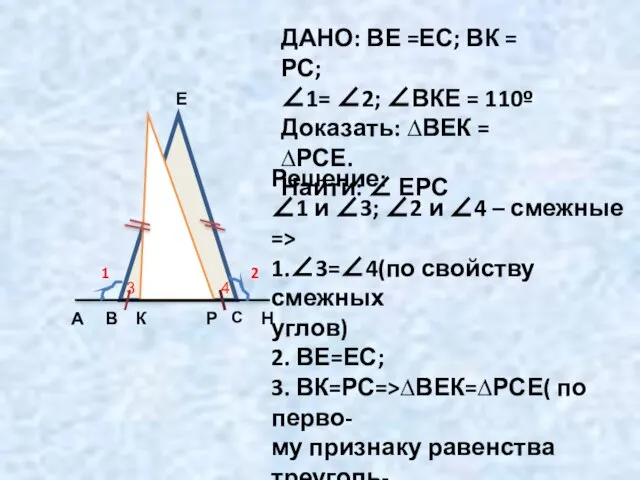
- 11. А В С Н К Е Р 1 2 ДАНО: ВЕ =ЕС; ВК = РС; ∠1=
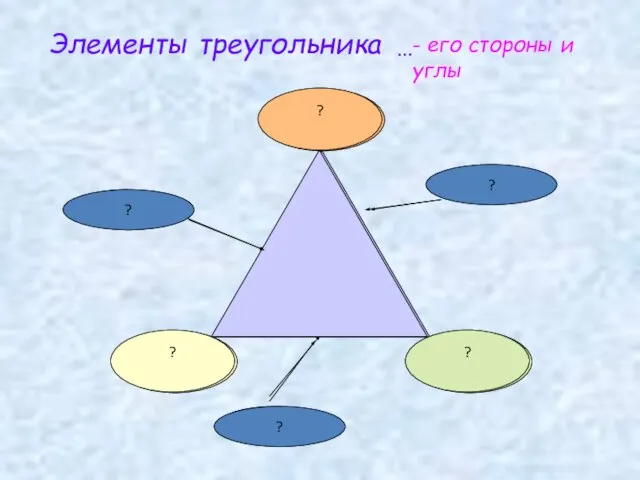
- 12. Сторона Сторона Сторона Элементы треугольника - его стороны и углы ? ? ? …
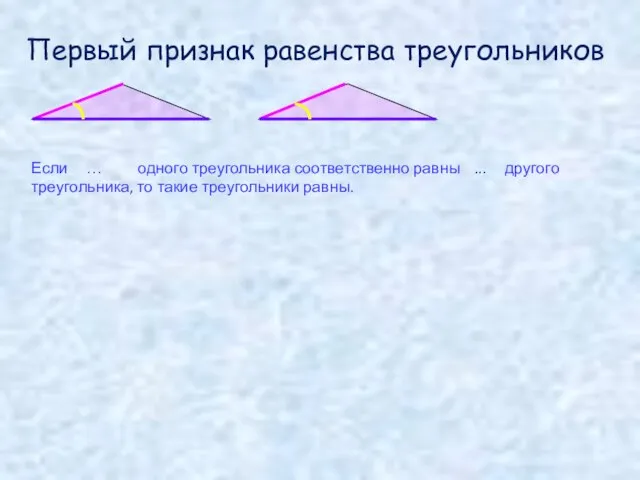
- 13. Если … одного треугольника соответственно равны ... другого треугольника, то такие треугольники равны. Первый признак равенства
- 14. Первый признак равенства треугольников
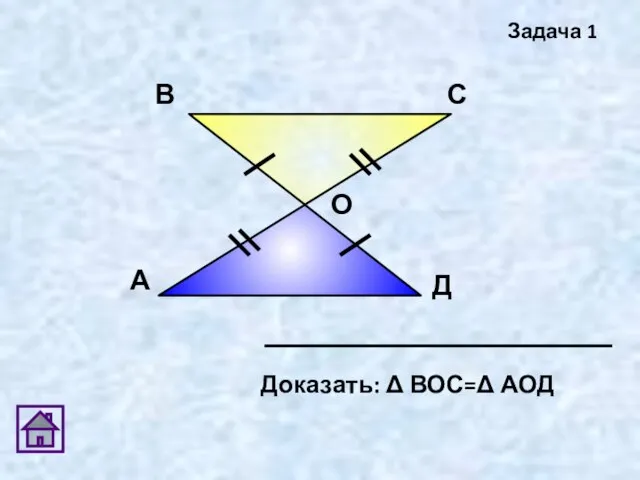
- 15. А В С Д О Задача 1
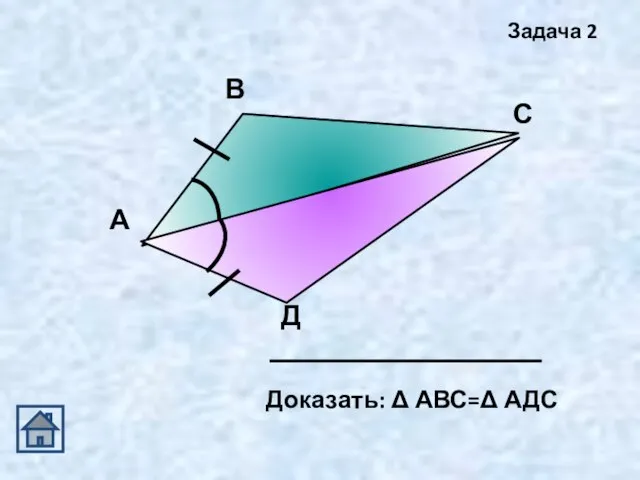
- 16. А В С Д Задача 2
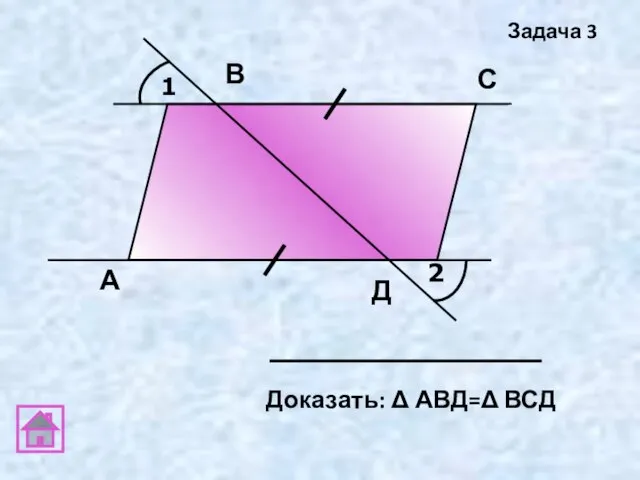
- 17. 1 2 А В С Д Задача 3
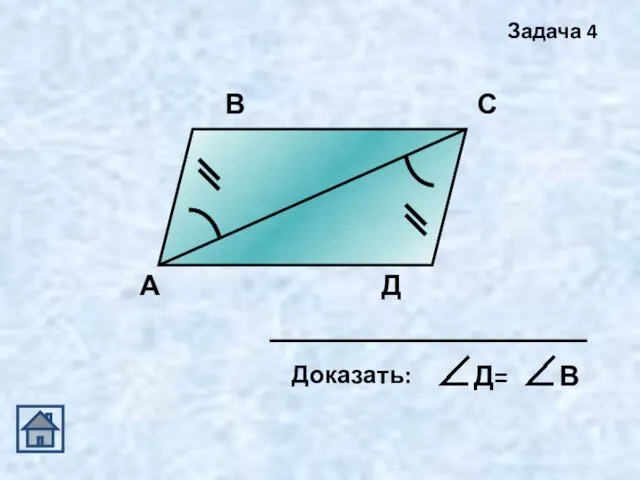
- 18. А В С Д Задача 4
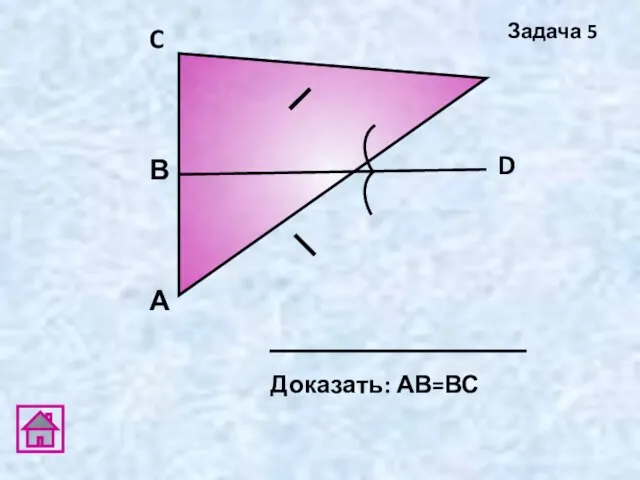
- 19. А D В C Доказать: АВ=ВС Задача 5
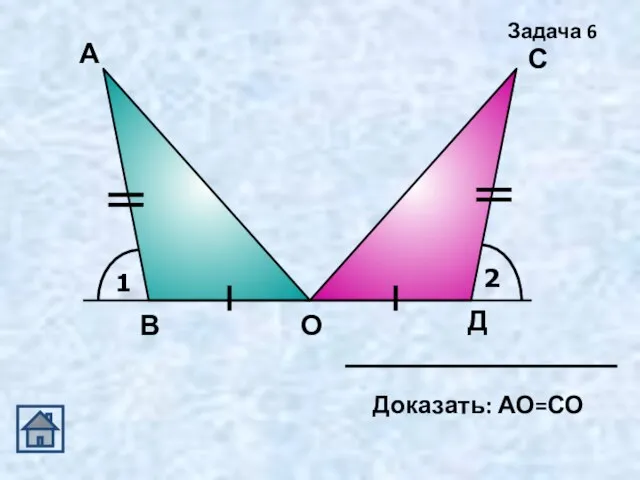
- 20. 1 2 А Д С О В Задача 6
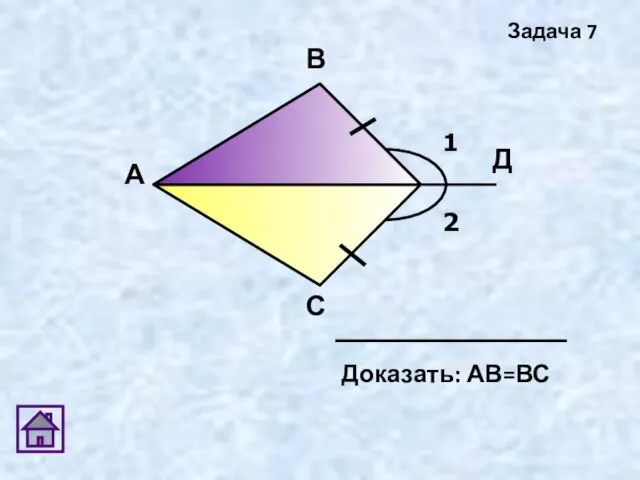
- 21. Задача 7
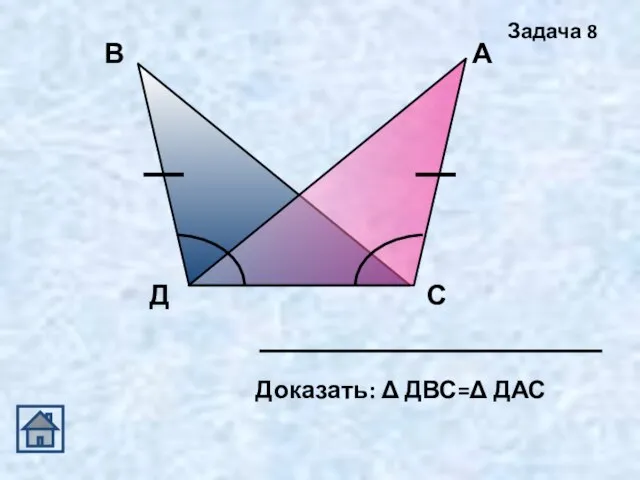
- 22. Доказать: Δ ДВС=Δ ДАС Задача 8
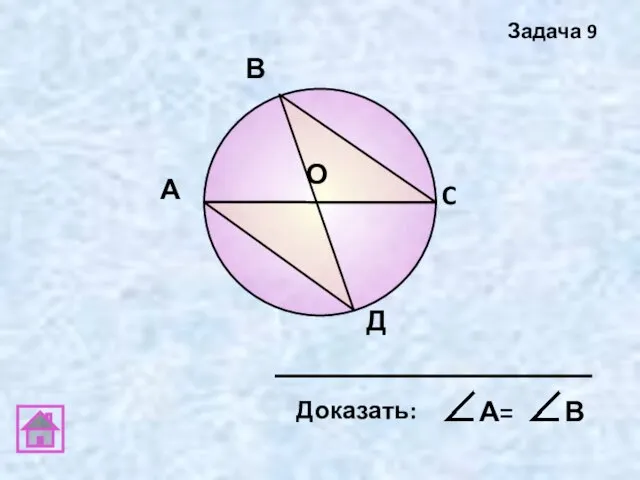
- 23. А В C Д О Задача 9
- 25. Скачать презентацию



 Симметрия в природе
Симметрия в природе Решение задач. Урок 22
Решение задач. Урок 22 Презентация на тему ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ
Презентация на тему ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ  Тест. Округление чисел до десятков, сотен
Тест. Округление чисел до десятков, сотен Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Умножение и деление дробей
Умножение и деление дробей Математика в лицах
Математика в лицах Решение задач на проценты. Концентрация
Решение задач на проценты. Концентрация Проценты. Проценты в древности
Проценты. Проценты в древности Многоэтажные дроби. 8 класс
Многоэтажные дроби. 8 класс Подготовка к контрольной работе
Подготовка к контрольной работе Естественно балансирующееся общество
Естественно балансирующееся общество Способы решения задач на смеси и сплавы
Способы решения задач на смеси и сплавы Дидактические материалы на уроках математики
Дидактические материалы на уроках математики Действия с величинами. Урок №4
Действия с величинами. Урок №4 Аксиомы стереометрии
Аксиомы стереометрии Практикум по решению задач
Практикум по решению задач Числовые функции
Числовые функции Сокращение дробей
Сокращение дробей Устное решение задач по готовым чертежам
Устное решение задач по готовым чертежам Аксиомы стереометрии
Аксиомы стереометрии Математическая викторина
Математическая викторина Решение показательных уравнений. 10 класс. Учебник С. М. Никольского
Решение показательных уравнений. 10 класс. Учебник С. М. Никольского Математическая статистика. Формула классической вероятности
Математическая статистика. Формула классической вероятности Площадь многоугольника
Площадь многоугольника Исследование функций и построение графиков
Исследование функций и построение графиков Основы теории вероятностей или случайные события ( лекция 2)
Основы теории вероятностей или случайные события ( лекция 2) Дисперсионный анализ
Дисперсионный анализ