Содержание
- 2. Рене Декарт Декартову систему координат вперше запропонував відомий французький математик Рене Декарт близько 1637р. у працях
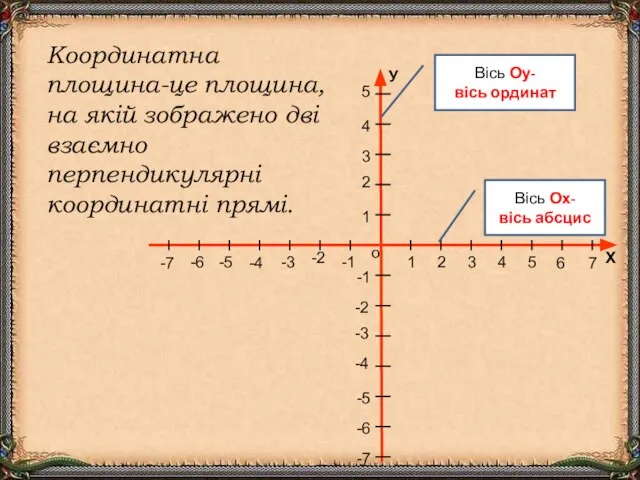
- 3. Рис. 1. Прямокутна система координат на площині О – початок координат; ОХ і ОУ – вісі
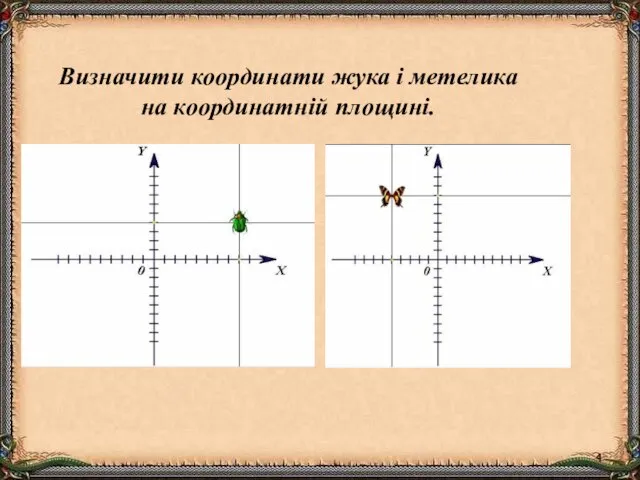
- 4. Визначити координати жука і метелика на координатній площині.
- 5. Х о У 1 2 3 4 5 1 2 3 4 5 -1 -2 -3
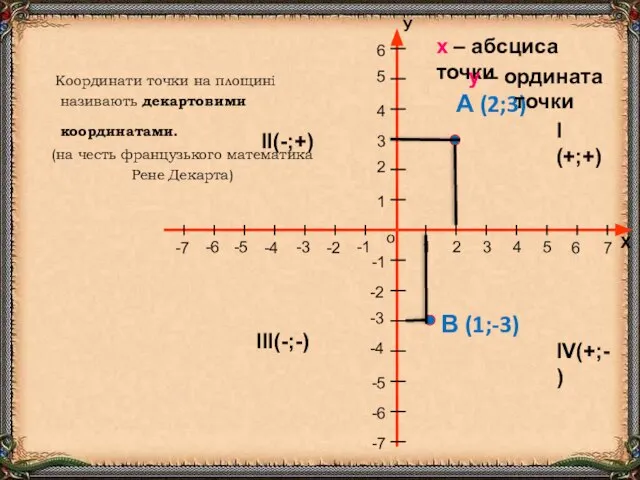
- 6. Координати точки на площині називають декартовими координатами. (на честь французького математика Рене Декарта) А (2;3) В
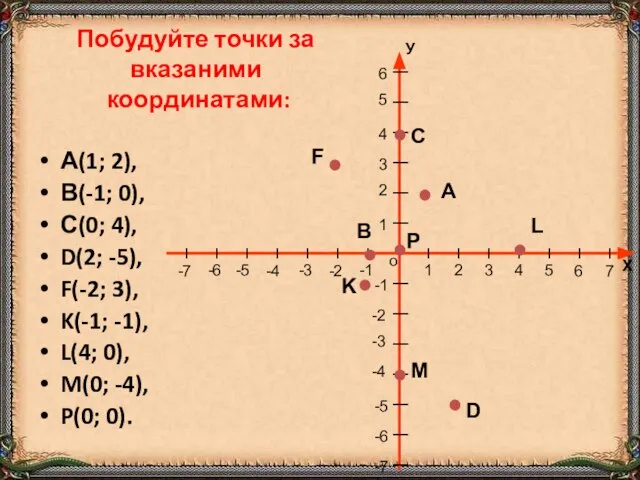
- 7. А(1; 2), В(-1; 0), С(0; 4), D(2; -5), F(-2; 3), K(-1; -1), L(4; 0), M(0; -4),
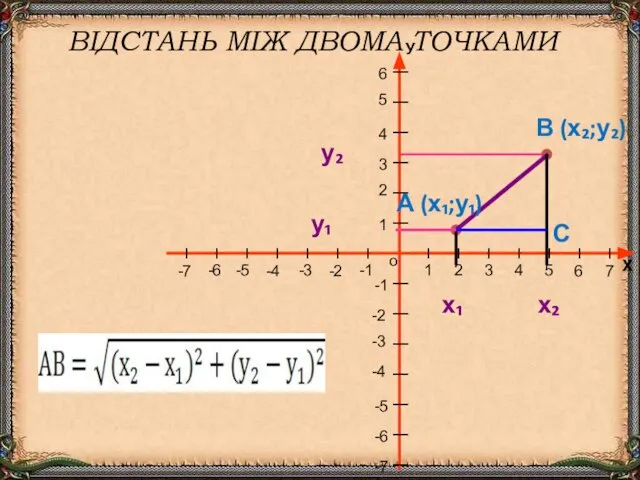
- 8. ВІДСТАНЬ МІЖ ДВОМА ТОЧКАМИ А (х₁;у₁) В (х₂;у₂) х₂ у₂ у₁ х₁ С
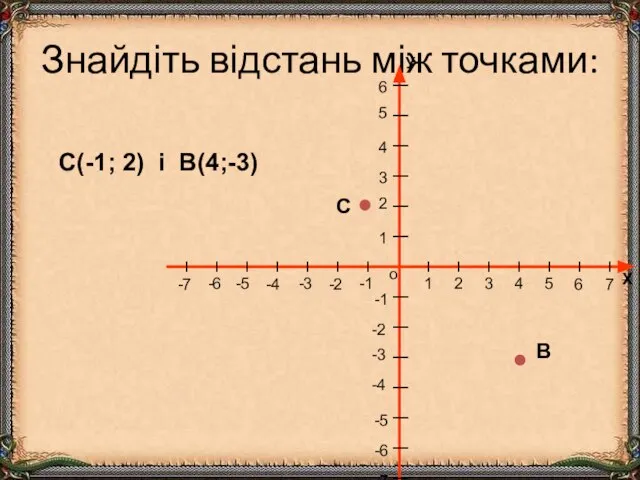
- 9. Знайдіть відстань між точками: С(-1; 2) і В(4;-3) С В
- 10. Знайдіть відстань між точками: С(-1; 2) і В(4;-3)
- 11. Вершинами трикутника є точки А(-1;3), В(5;9), С(6;2). Доведіть, що трикутник-рівнобедрений. ВС=АС, АВС- рівнобедрений.
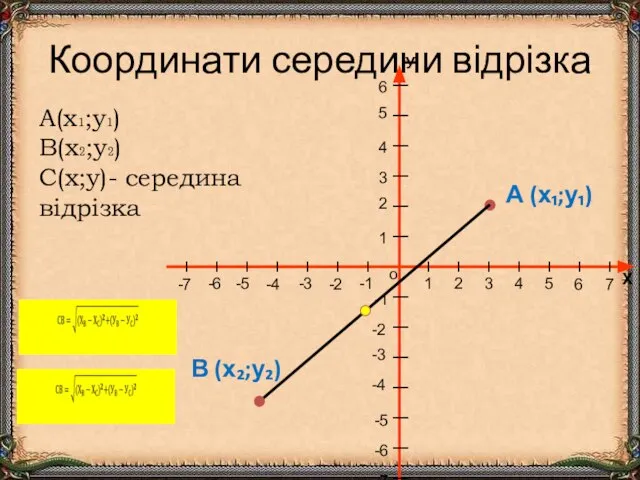
- 12. Координати середини відрізка А (х₁;у₁) В (х₂;у₂) А(х₁;у₁) В(х₂;у₂) С(х;у)- середина відрізка , а
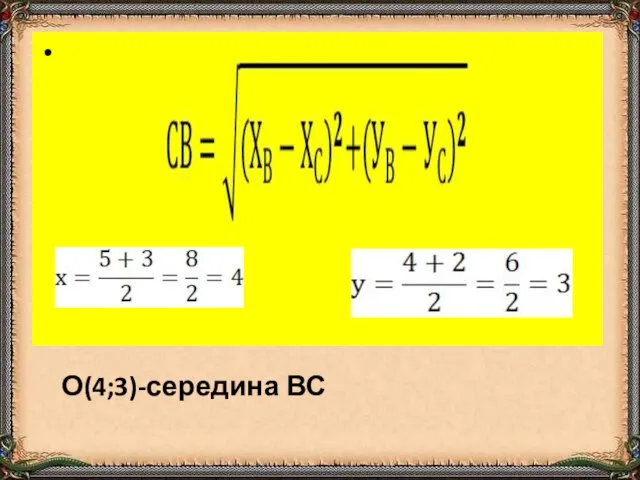
- 13. О(4;3)-середина ВС
- 15. Скачать презентацию




 Обучающие слайды
Обучающие слайды Многочлены над числовыми полями
Многочлены над числовыми полями Приёмы умножения числа 2
Приёмы умножения числа 2 Теория вероятностей
Теория вероятностей Математика. Занятие Число 7
Математика. Занятие Число 7 Где логика. Игра
Где логика. Игра Теорема Пифагора. Решение задач. Урок для 8 класса
Теорема Пифагора. Решение задач. Урок для 8 класса Математика в биологии
Математика в биологии Решение систем уравнений с двумя переменными методом подстановки
Решение систем уравнений с двумя переменными методом подстановки Презентация на тему КВН по математике
Презентация на тему КВН по математике  Задачи, обратные данной
Задачи, обратные данной Арифметическая игра. Чебурашка и числовые домики
Арифметическая игра. Чебурашка и числовые домики Арифметическая прогрессия
Арифметическая прогрессия Спецификация КИМ ЕГЭ 2015 г. Проверяемые требования (умения)
Спецификация КИМ ЕГЭ 2015 г. Проверяемые требования (умения) Модель Мальтуса
Модель Мальтуса Презентация на тему СЛОЖЕНИЕ ЧИСЕЛ С ПОМОЩЬЮ КООРДИНАТНОЙ ПРЯМОЙ
Презентация на тему СЛОЖЕНИЕ ЧИСЕЛ С ПОМОЩЬЮ КООРДИНАТНОЙ ПРЯМОЙ  Умножение двузначных чисел
Умножение двузначных чисел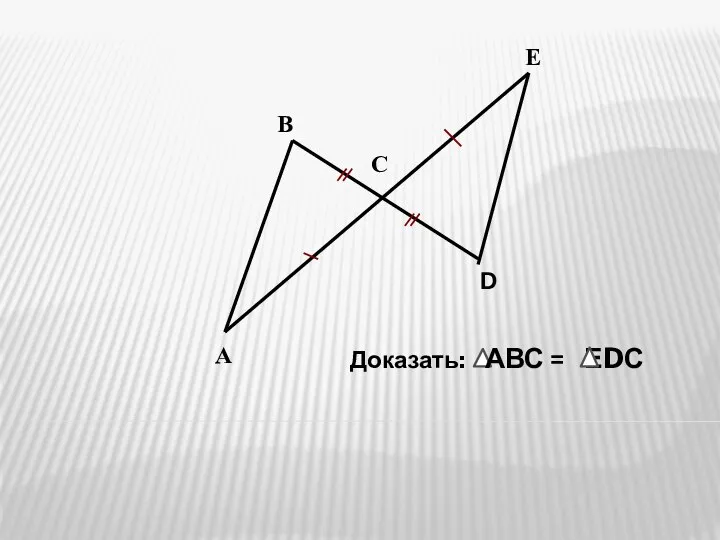 Признаки равенства треугольников. Решение задач
Признаки равенства треугольников. Решение задач Признак перпендикулярности прямой и плоскости
Признак перпендикулярности прямой и плоскости Фотоальбом. Ребус
Фотоальбом. Ребус Случайные величины. Классификация ошибок измерений. Абсолютная и относительная погрешность
Случайные величины. Классификация ошибок измерений. Абсолютная и относительная погрешность Согласование существительных с числительными
Согласование существительных с числительными Площади поверхностей и объёмы тел вращения
Площади поверхностей и объёмы тел вращения Алгоритм построения графиков, содержащих модуль
Алгоритм построения графиков, содержащих модуль Плоскость в пространстве
Плоскость в пространстве Арифметическая прогрессия. 9 класс
Арифметическая прогрессия. 9 класс Логарифмические уравнения и их системы
Логарифмические уравнения и их системы Центральные углы и углы, вписанные в окружность
Центральные углы и углы, вписанные в окружность