Содержание
- 2. Четырёхугольник — это геометрическая фигура, состоящая из четырёх точек, не лежащих на одной прямой, и четырёх
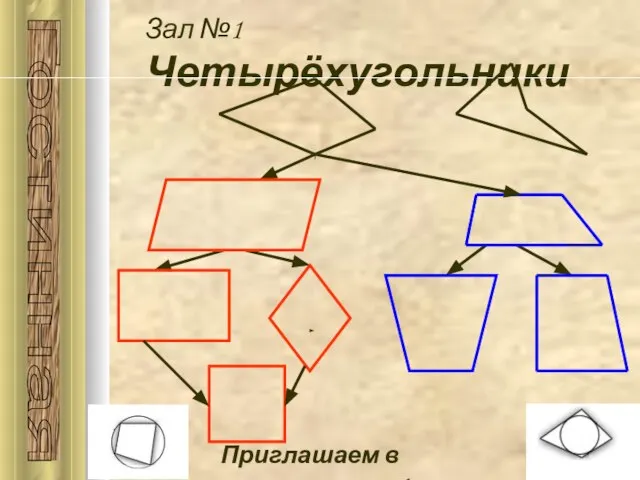
- 3. Зал №1 Четырёхугольники Гостинная Приглашаем в путешествие!
- 4. Если никакие стороны четырёхугольника не параллельны, то середина отрезка, соединяющего точки пересечения противоположных сторон, лежит на
- 5. Иоганн Карл Фри́дрих Га́усс (нем. Johann Carl Friedrich Gauß) 1777,Брауншвейг — 1855, Гёттинген. Немецкий математик, астроном
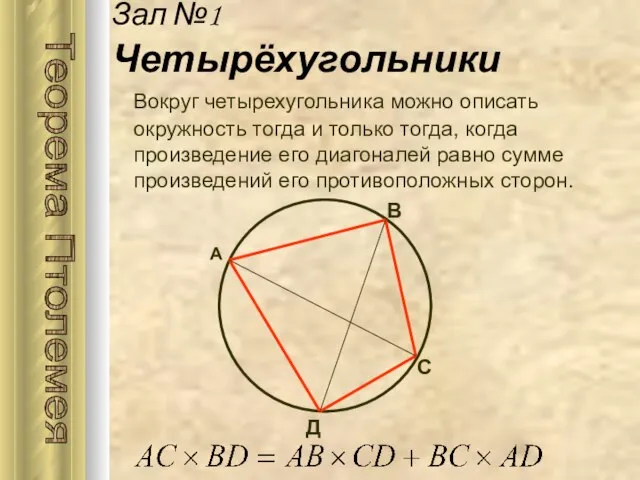
- 6. Вокруг четырехугольника можно описать окружность тогда и только тогда, когда произведение его диагоналей равно сумме произведений
- 7. Зал №1 Четырёхугольники Клавдий Птолемей, живший в конце первого — начале второго века н.э. Древнегреческий ученый
- 8. Зал №1 Четырёхугольники Если вписанный четырёхугольник имеет перпендикулярные диагонали, пересекающиеся в точке M, то прямая, проходящая
- 9. Зал №1 Четырёхугольники 00 0598 - 00 0660 индийский математик и астроном Брахмагупта Основные труды: «Брахма-спхута-сиддханта»
- 10. Зал №2 Параллелограмм (др.греч. παραλληλόγραμμον от παράλληλος — параллельный иγραμμή — линия) — это четырёхугольник, у
- 11. Зал №2 Параллелограмм В «Началах» Евклида доказывается следующая теорема: в параллелограмме противоположные стороны равны и противоположные
- 12. Зал №2 Параллелограмм Евкли́д или Эвкли́д (др.-греч. Εὐκλείδης, ок. 300 г. до н. э.) Древнегреческий математик.
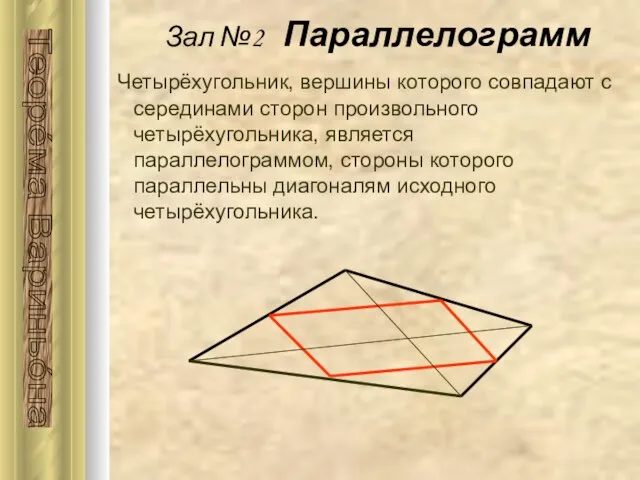
- 13. Четырёхугольник, вершины которого совпадают с серединами сторон произвольного четырёхугольника, является параллелограммом, стороны которого параллельны диагоналям исходного
- 14. Зал №2 Параллелограмм Учёный Пьер Вариньон (фр. Pierre Varignon, Кан, 1654 —1722, Париж) Французский математик ,
- 15. Зал №3 Трапеция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого
- 16. Зал №2 Трапеция Посидоний — родился в Апамее в Сирии в 135 г., умер в Риме
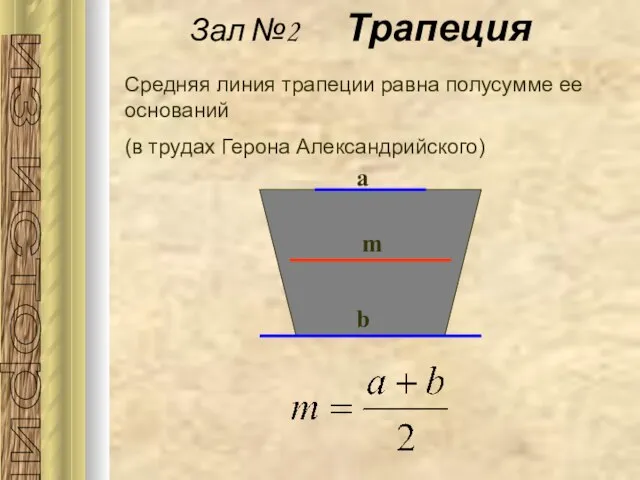
- 17. Средняя линия трапеции равна полусумме ее оснований (в трудах Герона Александрийского) Зал №2 Трапеция из истории
- 18. Зал №3 Трапеция Герон Александрийский (Heron, I в. н. э.) Греческий механик и математик. Занимался геометрией,
- 19. Зал №4 Ромб Термин «ромб» происходит от др.-греч. ῥόμβος — «бубен». Слово «ромб» впервые употребляется у
- 20. Зал №4 Ромб «Собрание» (συναγωγή). Автор Папп Александри́йский (др.-греч. Πάππος ὁ Ἀλεξανδρεύς) — древнегреческий математик второй
- 21. Мозаика Пенроуза, плитки Пенроуза -непериодическое разбиение плоскости, апериодические регулярные структуры, замощение плоскости ромбами двух типов —
- 22. Зал №5 Прямоугольник Прямоугольник (перевод с греч. ορθογώνιο.) Этимология Первые геометры мыслили прямоугольник вписанным в круг
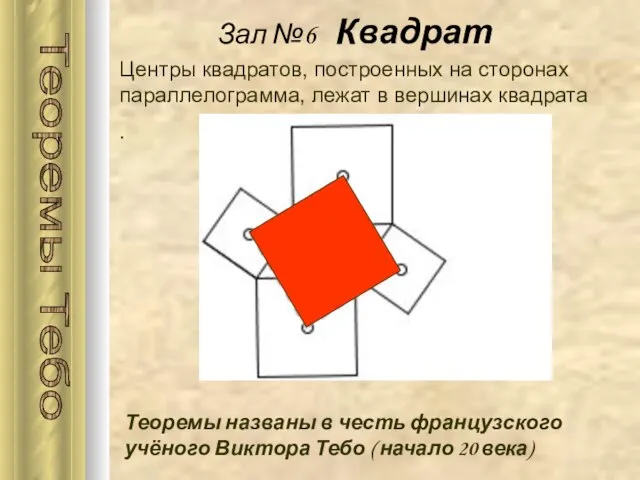
- 23. Зал №6 Квадрат От латинского quadratum (quadrare - сделать четырехугольным), перевод с греческого “тетрагонон” - четырехугольник.
- 24. Центры квадратов, построенных на сторонах параллелограмма, лежат в вершинах квадрата . Зал №6 Квадрат Теоремы Тебо
- 25. Теоремы Тебо Зал №6 Квадрат Если на каждой из двух соседних сторон квадрата построить по равностороннему
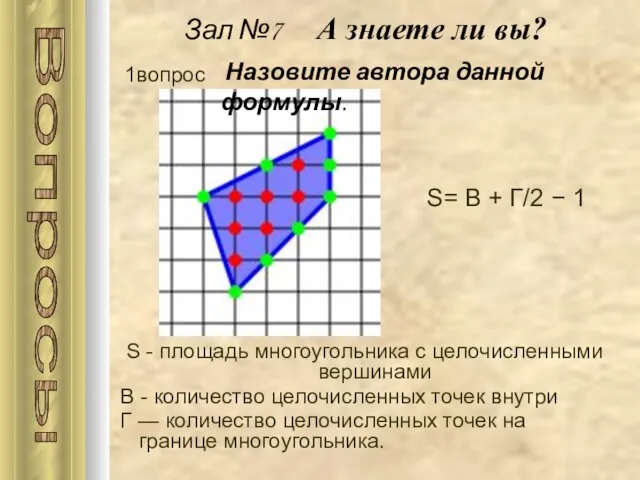
- 26. Зал №7 А знаете ли вы? S - площадь многоугольника с целочисленными вершинами В - количество
- 27. Зал №7 А знаете ли вы? 2 вопрос Какая фигура называется дельтоидом? 3 вопрос Какая мышца
- 29. Скачать презентацию




















 Многогранники
Многогранники Четырехугольники
Четырехугольники Пентагон
Пентагон Площади фигур. Зачёт
Площади фигур. Зачёт Первый признак равенства треугольников
Первый признак равенства треугольников Теорема косинусов
Теорема косинусов Правильные многоугольники (9 класс)
Правильные многоугольники (9 класс) Графическое решение квадратных уравнений
Графическое решение квадратных уравнений Луч и угол (7 класс)
Луч и угол (7 класс) Объём призмы
Объём призмы Итоговое повторение курса геометрии
Итоговое повторение курса геометрии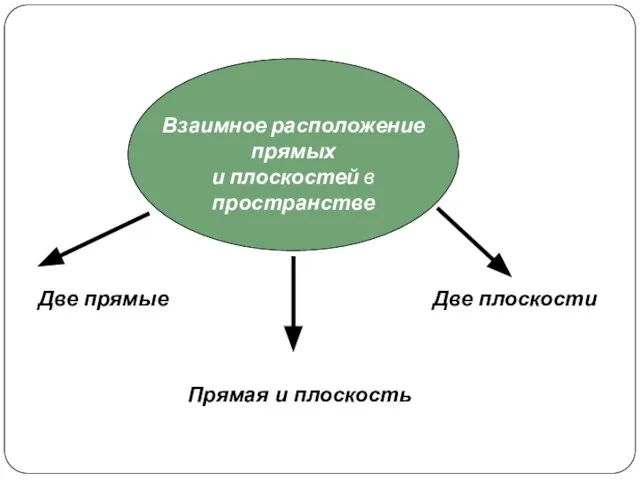 Взаимное расположение прямых и плоскостей в пространстве
Взаимное расположение прямых и плоскостей в пространстве Жевачевская Анна Валентиновна Учитель математики/информатики МБОУ СОШ №151 г.Новосибирска
Жевачевская Анна Валентиновна Учитель математики/информатики МБОУ СОШ №151 г.Новосибирска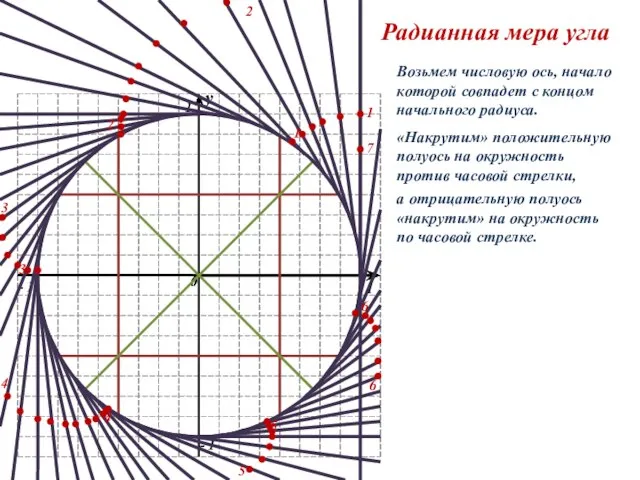 Радианная мера угла
Радианная мера угла Карточки - задания по теме "Конус"
Карточки - задания по теме "Конус" «Чтение графиков. ЕГЭ» ЮВАО
«Чтение графиков. ЕГЭ» ЮВАО Почему квадрат?
Почему квадрат? Объем тел вращения - презентация по Геометрии
Объем тел вращения - презентация по Геометрии ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ
ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ Проецирование (8 класс)
Проецирование (8 класс) Биссектриса угла
Биссектриса угла Параллельные прямые
Параллельные прямые Теорема Пифагора. Приминение
Теорема Пифагора. Приминение Периметр. Площа - презентация по Геометрии_
Периметр. Площа - презентация по Геометрии_ Сложение, вычитание, умножение, деление натуральных чисел. Угол, треугольник, прямоугольник
Сложение, вычитание, умножение, деление натуральных чисел. Угол, треугольник, прямоугольник Чудеса симметрии
Чудеса симметрии Длина отрезка
Длина отрезка Скалярное произведение векторов
Скалярное произведение векторов