Содержание
- 2. Нахождение угла между скрещивающимися прямыми Данная тема актуальна, так как подобные задачи требуют развитого абстрактного мышления.
- 3. Аргументы. 1). Определение скрещивающихся прямых. 2). Определение угла между скрещивающимися прямыми. 3). Признак скрещивающихся прямых. 4).
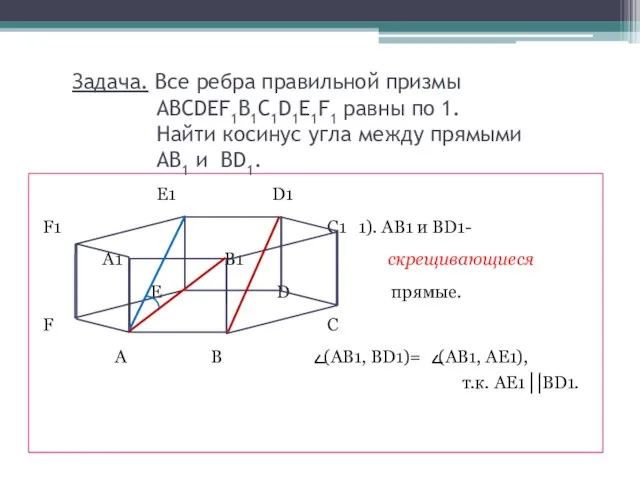
- 4. Задача. Все ребра правильной призмы ABCDEF1B1C1D1E1F1 равны по 1. Найти косинус угла между прямыми AB1 и
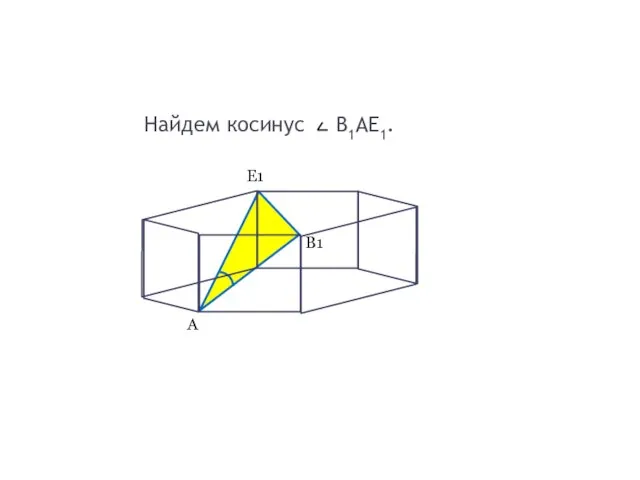
- 5. Найдем косинус B1AE1. А В1 Е1
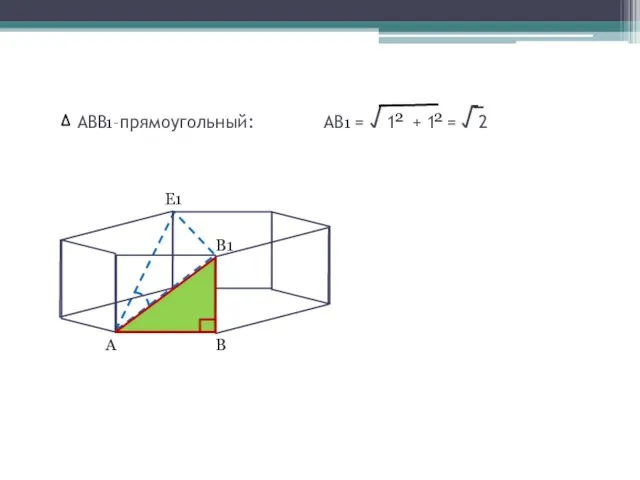
- 6. АВВ –прямоугольный: АВ = √1 + 1 = √2 1 1 2 2 А В1 В
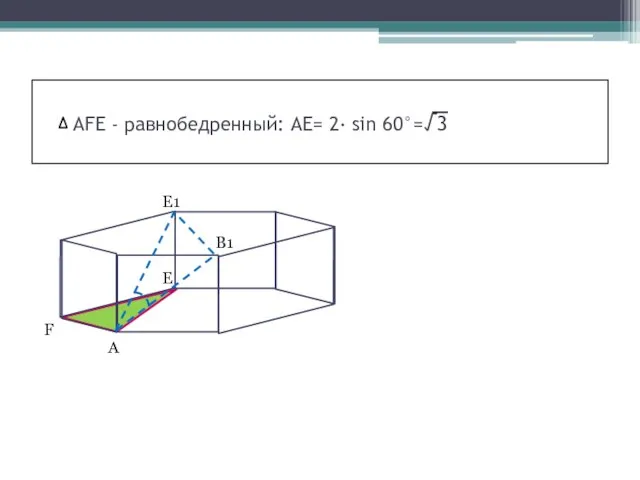
- 7. AFE - равнобедренный: АЕ= 2· sin 60°=√3 F A E E1 В1
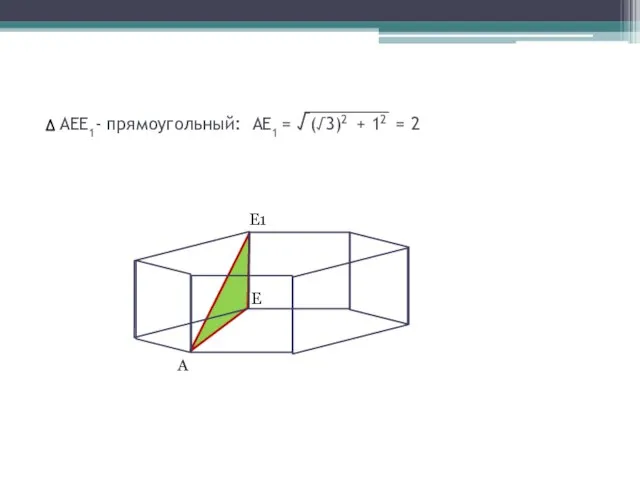
- 8. AEE1- прямоугольный: АЕ1 = √(√3)2 + 12 = 2 E1 A E
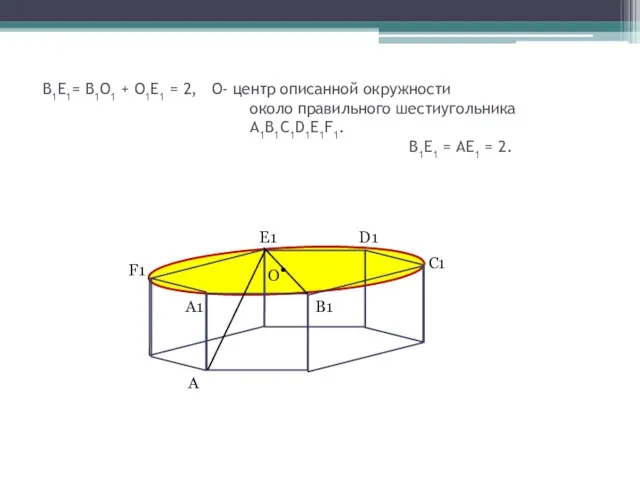
- 9. В1Е1= В1О1 + О1Е1 = 2, О- центр описанной окружности около правильного шестиугольника A1B1C1D1E1F1. В1Е1 =
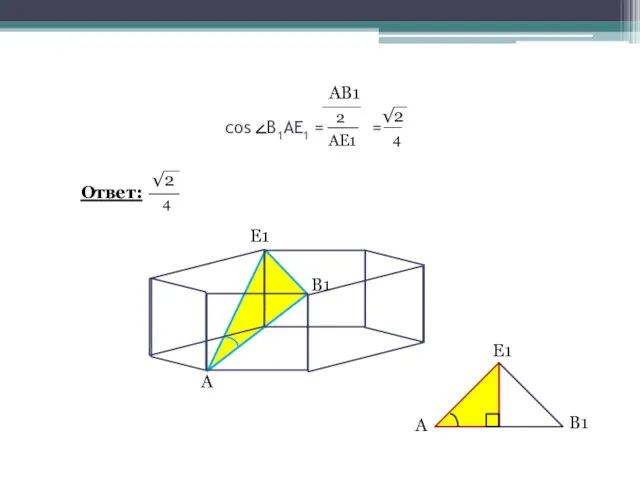
- 10. cos В1АЕ1 = = А В1 Е1 А В1 Е1 Ответ:
- 12. Скачать презентацию


 Смежные и вертикальные углы
Смежные и вертикальные углы Перпендикулярные прямые в пространстве
Перпендикулярные прямые в пространстве Площади фигур. Теорема Пифагора
Площади фигур. Теорема Пифагора Разные способы нахождения площади многоугольников
Разные способы нахождения площади многоугольников Определение параллельных прямых
Определение параллельных прямых Площадь 8 КЛАСС
Площадь 8 КЛАСС Решение задач по геометрии на готовых чертежах
Решение задач по геометрии на готовых чертежах Косинус
Косинус Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Учитель математики ГБОУ СОШ№1168 г. Москвы Мишина Раиса Михайловна
Учитель математики ГБОУ СОШ№1168 г. Москвы Мишина Раиса Михайловна Сопряжение. Геометрические построения - презентация по Геометрии_
Сопряжение. Геометрические построения - презентация по Геометрии_ Приращение функции и приращение аргумента
Приращение функции и приращение аргумента Биссектриса угла
Биссектриса угла Решение задач на вычисление площадей фигур
Решение задач на вычисление площадей фигур Двугранные углы - презентация по Геометрии_
Двугранные углы - презентация по Геометрии_ Построение геометрических тел
Построение геометрических тел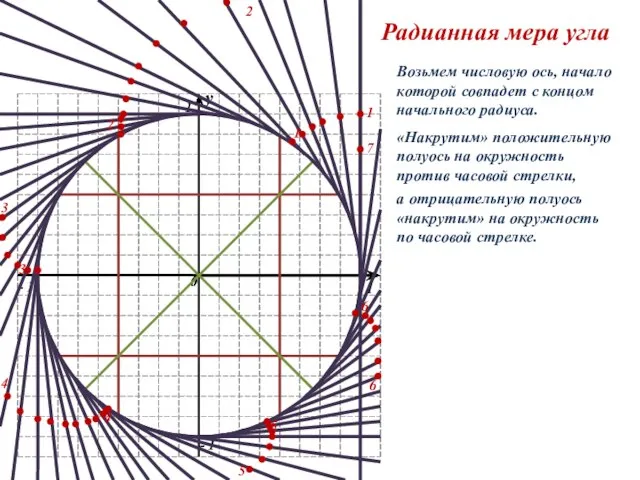 Радианная мера угла
Радианная мера угла Прямоугольник
Прямоугольник Координаты вектора
Координаты вектора Координатный метод
Координатный метод Скрещивающиеся прямые. Углы с сонаправленными сторонами. Угол между прямыми
Скрещивающиеся прямые. Углы с сонаправленными сторонами. Угол между прямыми Векторы
Векторы Векторы на плоскости и в пространстве, векторный метод решения задач
Векторы на плоскости и в пространстве, векторный метод решения задач Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год.
Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год. Простейшие задачи в координатах
Простейшие задачи в координатах Объём призмы
Объём призмы От египетского треугольника до Пифагора
От египетского треугольника до Пифагора Взаимное положение прямых Начертательная геометрия 11 класс
Взаимное положение прямых Начертательная геометрия 11 класс