Содержание
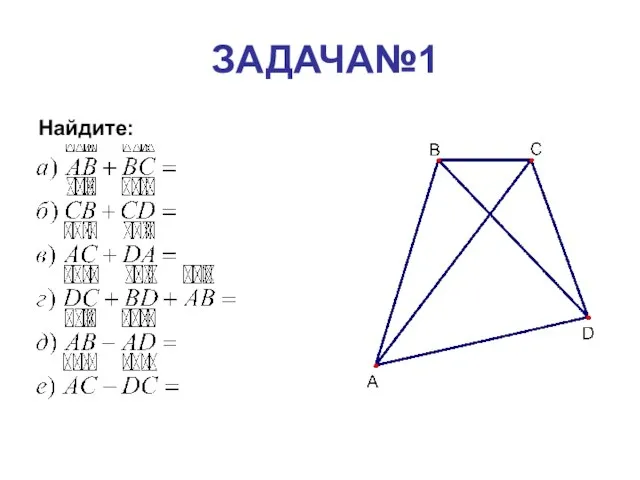
- 2. ЗАДАЧА№1 Найдите:
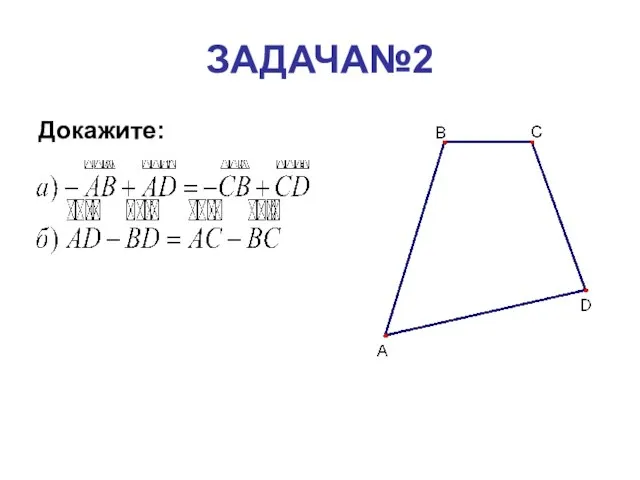
- 3. ЗАДАЧА№2 Докажите:
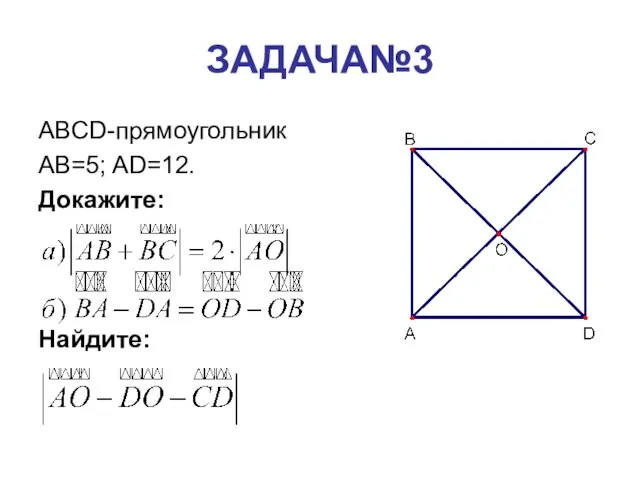
- 4. ЗАДАЧА№3 ABCD-прямоугольник AB=5; AD=12. Докажите: Найдите:
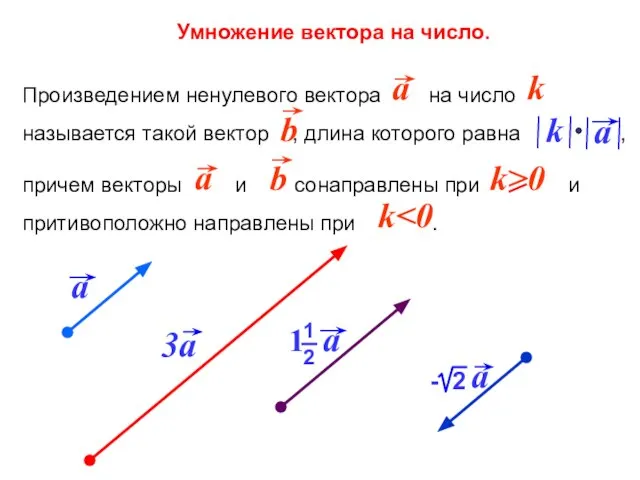
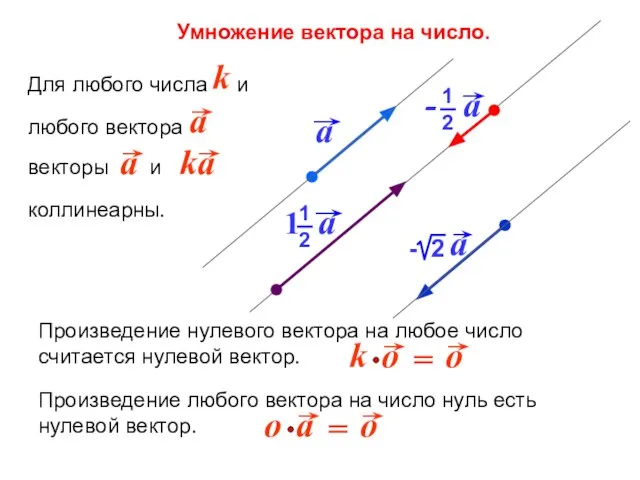
- 5. Умножение вектора на число.
- 6. Умножение вектора на число.
- 7. Умножение вектора на число. Произведение любого вектора на число нуль есть нулевой вектор. Произведение нулевого вектора
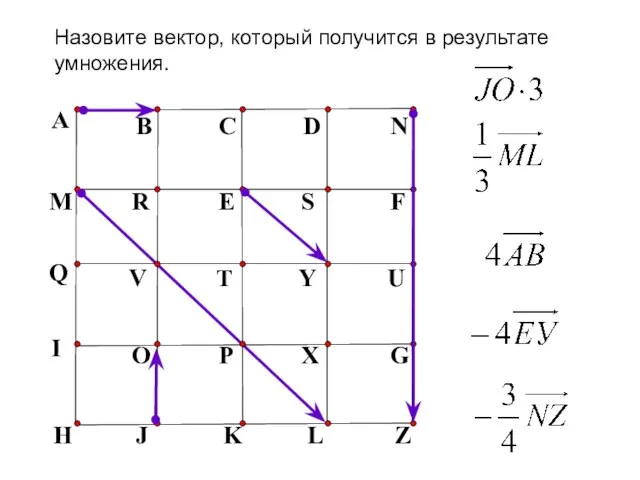
- 8. A B C D N M R E S F H J K L Z Q
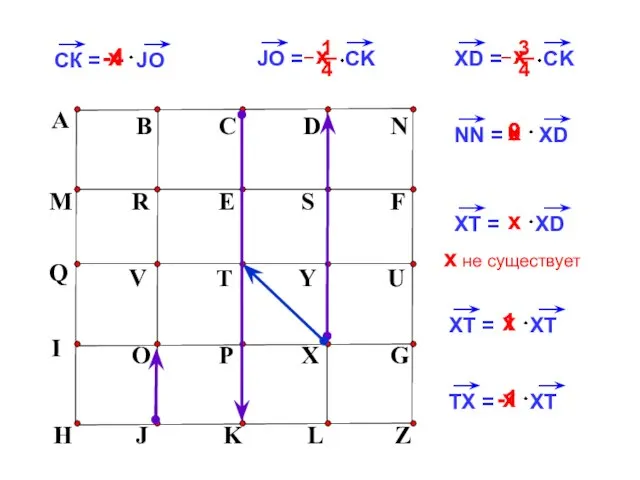
- 9. х -4 0 х A B C D N M R E S F H J
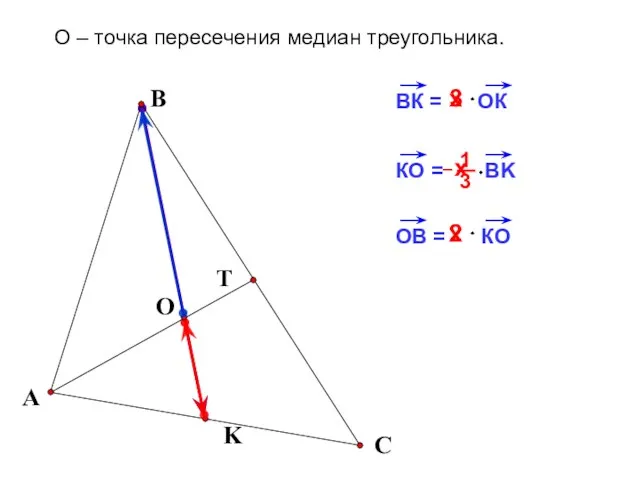
- 10. 2 х 3 A C O K T B О – точка пересечения медиан треугольника. х
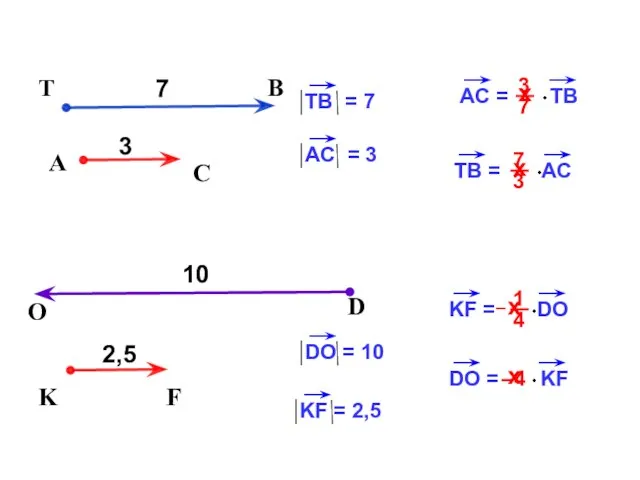
- 11. х –4 A C 7 T B х 3 х х
- 12. х 1,25 A C T B ТВ = АС х Длина вектора TB на 25% больше
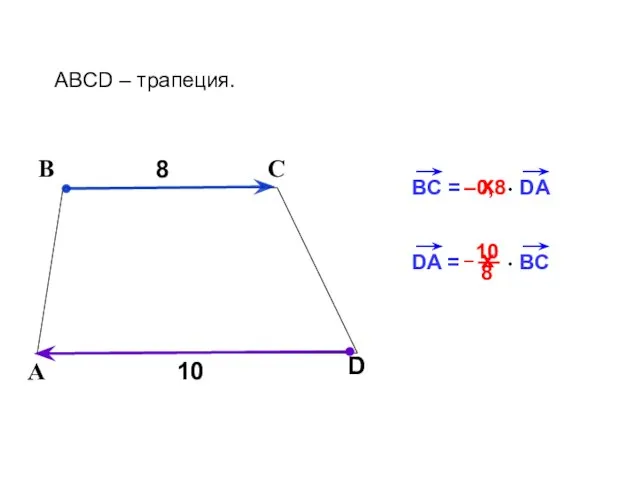
- 13. BC = DA 8 В С ABCD – трапеция. А D 10 х –0,8 DA =
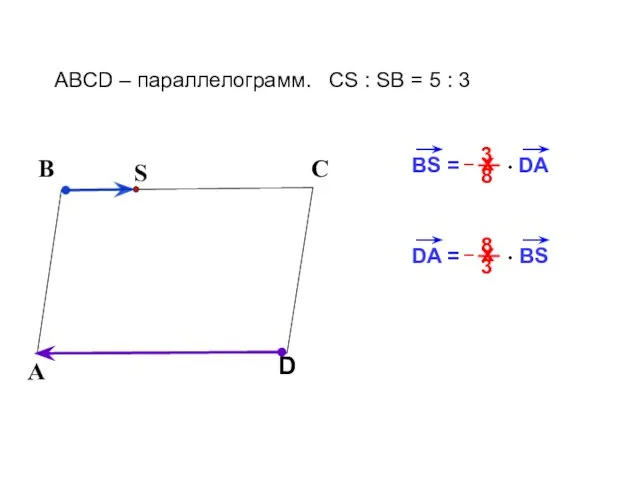
- 14. В С ABCD – параллелограмм. CS : SB = 5 : 3 А D BS =
- 15. Умножение вектора на число обладает следующими основными свойствами. Сочетательный закон Первый распределительный закон Второй распределительный закон
- 16. Рисунок иллюстрирует сочетательный закон. Представлен случай, когда k = 2, l = 3. Сочетательный закон 1
- 17. B Рисунок иллюстрирует первый распределительный закон. Представлен случай, когда k = 3, l = 2. O
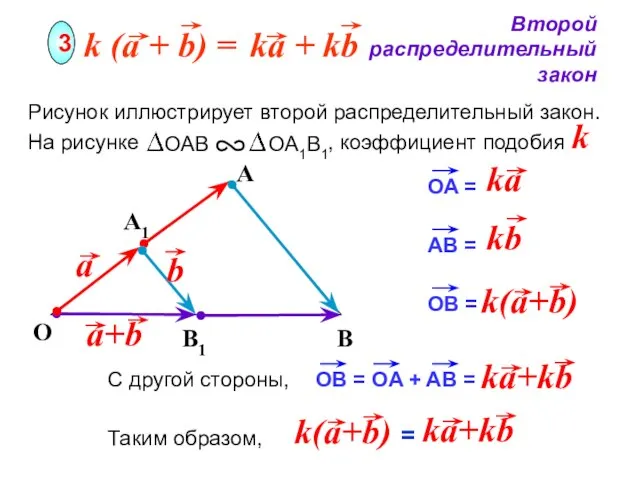
- 18. O Второй распределительный закон 3 A Рисунок иллюстрирует второй распределительный закон. На рисунке , коэффициент подобия
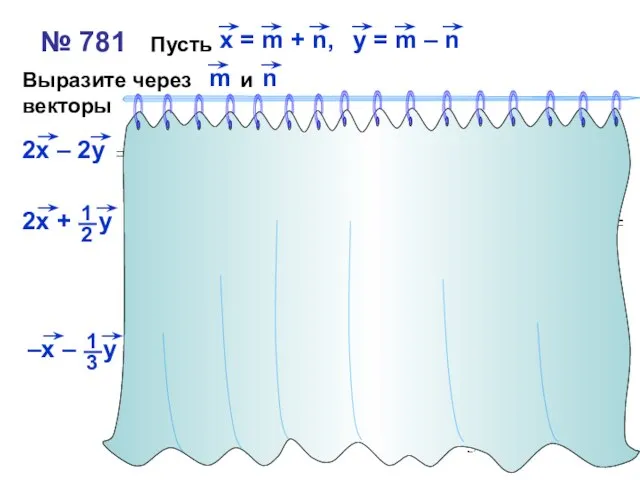
- 19. № 781 Пусть Выразите через и векторы
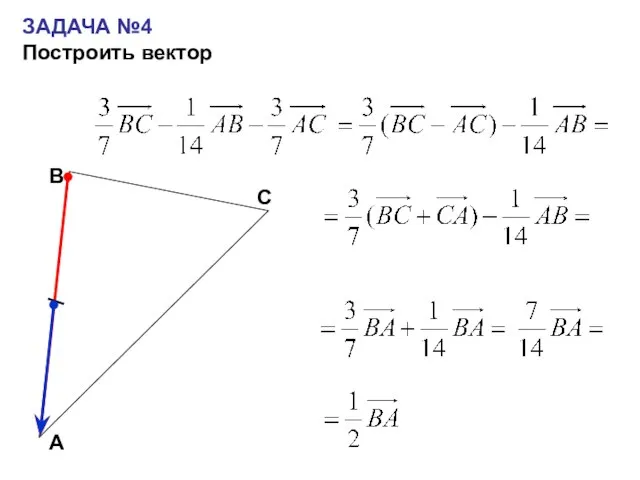
- 20. ЗАДАЧА №4 Построить вектор С А В
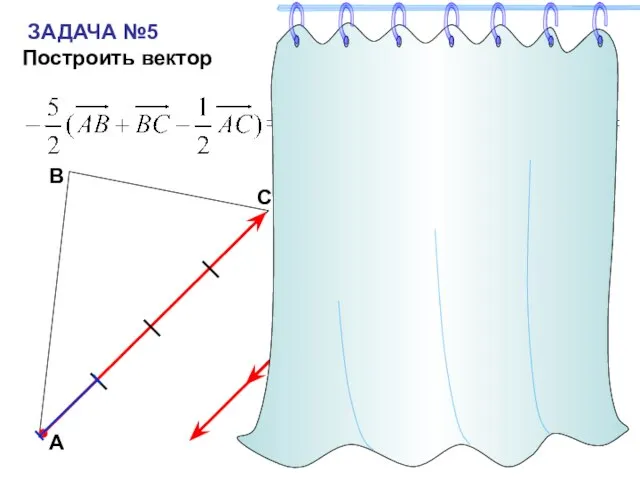
- 21. ЗАДАЧА №5 Построить вектор С А В
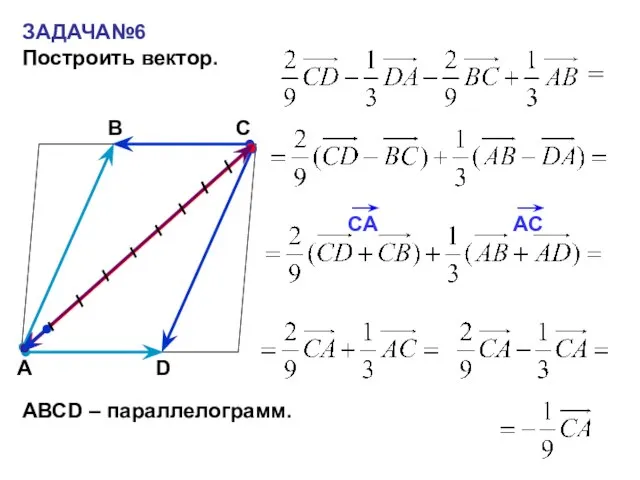
- 22. ЗАДАЧА№6 Построить вектор. С А В = АВСD – параллелограмм. D
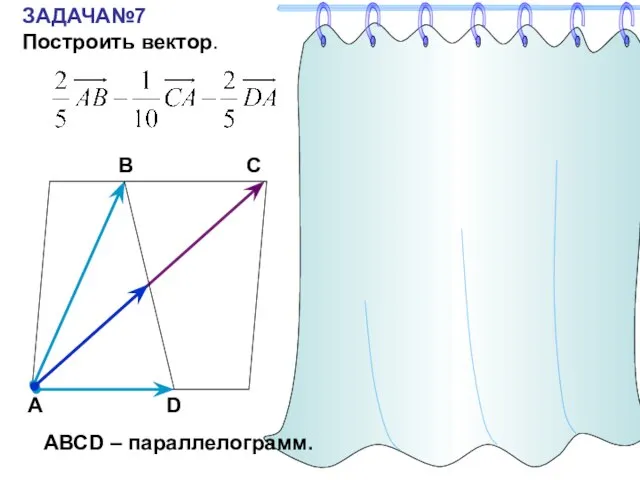
- 23. ЗАДАЧА№7 Построить вектор. С А В D АВСD – параллелограмм.
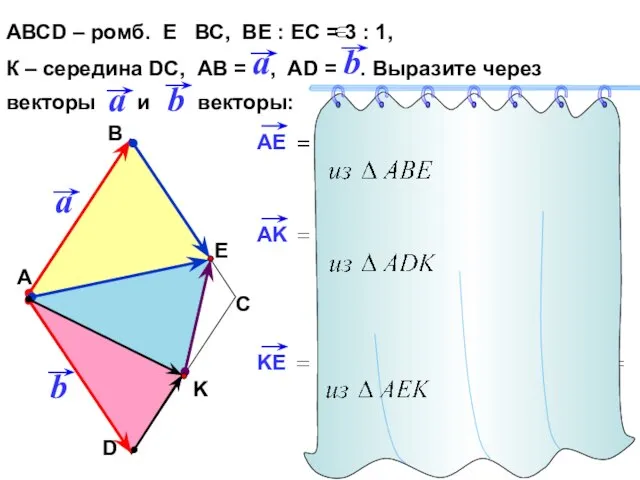
- 24. АВСD – ромб. Е ВС, ВЕ : ЕС = 3 : 1, К – середина DC,
- 26. Скачать презентацию





 Планиметрия - презентация по Геометрии_
Планиметрия - презентация по Геометрии_ Решение комбинированных задач с помощью графов
Решение комбинированных задач с помощью графов Фракталы – геометрия природы
Фракталы – геометрия природы Решение задач. Теорема о трех перпендикулярах.
Решение задач. Теорема о трех перпендикулярах. Признаки равенства треугольников 7 класс
Признаки равенства треугольников 7 класс Шар
Шар Многообразие многоугольников
Многообразие многоугольников Знакомство с миром геометрии
Знакомство с миром геометрии Площадь многоугольника 8 класс
Площадь многоугольника 8 класс Графы и их применение
Графы и их применение Курсовая работа слушателя курсов «Информационно - коммуникационное сопровождение обучения математике» Савицкой Галины Ивановны
Курсовая работа слушателя курсов «Информационно - коммуникационное сопровождение обучения математике» Савицкой Галины Ивановны Развёртка куба
Развёртка куба Двугранный угол. Признак перпендикулярности двух плоскостей
Двугранный угол. Признак перпендикулярности двух плоскостей Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда Полезные теоремы, следствия и задачи.
Полезные теоремы, следствия и задачи. Объём призмы
Объём призмы Геометрические построения на плоскости
Геометрические построения на плоскости Прямоугольный треугольник 8 класс - презентация по Геометрии___________________________________________________________________________________________________________________
Прямоугольный треугольник 8 класс - презентация по Геометрии___________________________________________________________________________________________________________________ Объем конуса
Объем конуса Геометрия Лобачевского
Геометрия Лобачевского Геометрия в архитектуре
Геометрия в архитектуре Золотое сечение в геометрии - презентация по Геометрии_
Золотое сечение в геометрии - презентация по Геометрии_ Урок повторения в 6 классе
Урок повторения в 6 классе Многогранники и кристаллы
Многогранники и кристаллы Симметрия. Осевая и центральная симметрии
Симметрия. Осевая и центральная симметрии Площадь треугольника. Полезные теоремы, следствия и задачи
Площадь треугольника. Полезные теоремы, следствия и задачи Осевая симметрия (6 класс)
Осевая симметрия (6 класс) Основные формулы тригонометрии
Основные формулы тригонометрии