Содержание
- 2. ВСПОМНИТЬ, ЧТО ТАКОЕ ПИРАМИДА НАУЧИТЬСЯ ПОЛЬЗОВАТЬСЯ ФОРМУЛОЙ НАХОЖДЕНИЯ ОБЪЁМА ПИРАМИДЫ Цель работы:
- 3. ЧТО ТАКОЕ ПИРАМИДА ТЕОРЕМА ДОКАЗАТЕЛЬСТВО СЛЕДСТВИЕ ЗАМЕЧАНИЕ ЗАДАЧИ ДЛЯ РЕШЕНИЯ ВЫВОД План:
- 4. ПИРАМИДА Пирамида – это многогранник, одной из граней которой служит многоугольник, а остальные грани – треугольники
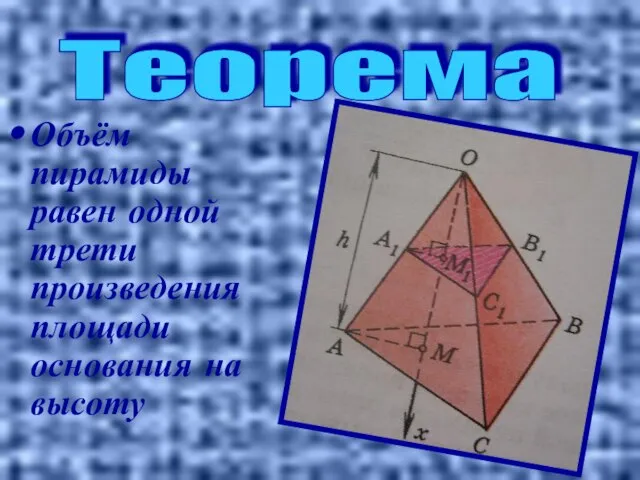
- 5. Объём пирамиды равен одной трети произведения площади основания на высоту Теорема
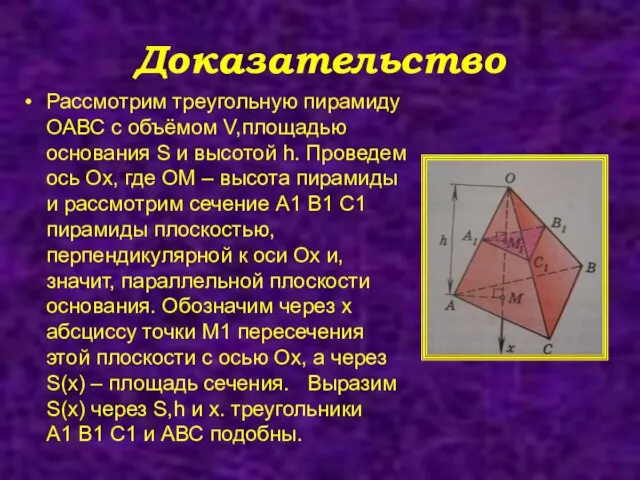
- 6. Доказательство Рассмотрим треугольную пирамиду ОАВС с объёмом V,площадью основания S и высотой h. Проведем ось Ох,
- 7. А1В1 параллельна АВ, поэтому треугольники ОА1В1 И ОАВ подобны. Следовательно, А1В1/АВ=ОА1/ОА. Прямоугольные треугольники ОА1М1 и ОАМ
- 8. Применяя теперь основную формулу для вычисления объемов тел при а=0, b=h, получаем
- 9. Докажем теперь терему для произвольной пирамиды с высотой h и площадью основания S. Такую пирамиду можно
- 10. Объем V усеченной пирамиды, высота которой равна h, а площади оснований равны S и S1, вычисляется
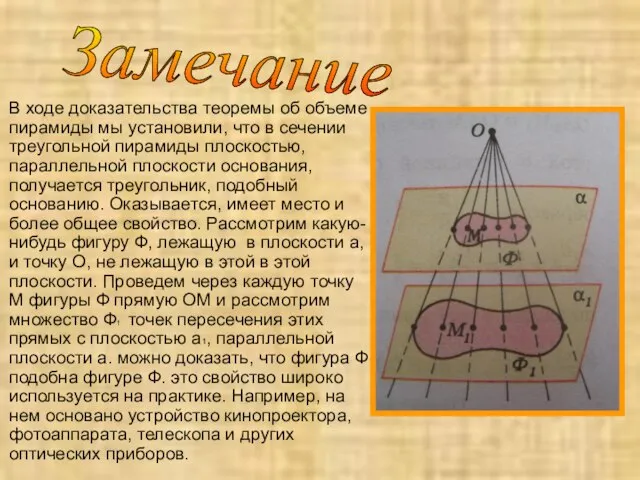
- 11. В ходе доказательства теоремы об объеме пирамиды мы установили, что в сечении треугольной пирамиды плоскостью, параллельной
- 12. №1 Найдите объем правильной треугольной пирамиды, высота которой равна 12 см, а сторона основания равна 13
- 13. Мы вспомнили, что такое пирамида, научились пользоваться формулой нахождения объема пирамиды. Вывод
- 14. СПАСИБО ЗА ПРОСМОТР!!!
- 16. Скачать презентацию










 ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ Петрова Людмила Анатольевна, учитель математики, г.Санкт-Петербург, лицей № 1
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ Петрова Людмила Анатольевна, учитель математики, г.Санкт-Петербург, лицей № 1 Треугольник Устные задачи
Треугольник Устные задачи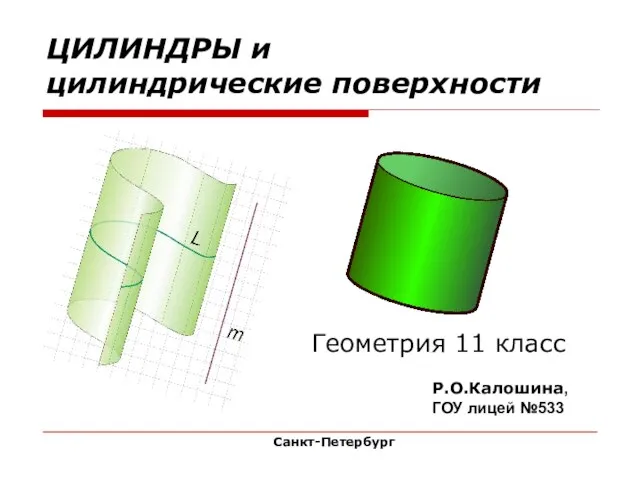 ЦИЛИНДРЫ и цилиндрические поверхности
ЦИЛИНДРЫ и цилиндрические поверхности Параллелограмм
Параллелограмм Векторы на плоскости и в пространстве, векторный метод решения задач
Векторы на плоскости и в пространстве, векторный метод решения задач Двумерный симплекс история его изучения
Двумерный симплекс история его изучения Вычисление угла между прямыми и плоскостями
Вычисление угла между прямыми и плоскостями Сопряжение. Геометрические построения - презентация по Геометрии_
Сопряжение. Геометрические построения - презентация по Геометрии_ Симметрия. Осевая и центральная симметрии
Симметрия. Осевая и центральная симметрии Положение плоскости относительно плоскостей проекций
Положение плоскости относительно плоскостей проекций Свойство биссектрисы угла треугольника
Свойство биссектрисы угла треугольника Правильная пирамида
Правильная пирамида Что такое окружность? - презентация по Геометрии_
Что такое окружность? - презентация по Геометрии_ Задания на клетчатой бумаге
Задания на клетчатой бумаге Внешний угол треугольника 7 класс - презентация_
Внешний угол треугольника 7 класс - презентация_ Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним
Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним Амидекстр
Амидекстр Параллельность и перпендикулярность прямых и плоскостей в пространстве
Параллельность и перпендикулярность прямых и плоскостей в пространстве Геометрия Лобачевского
Геометрия Лобачевского Геометрические задачи на экстремум
Геометрические задачи на экстремум Биссектриса угла
Биссектриса угла Что изучает геометрия 7 класс
Что изучает геометрия 7 класс Пирамиды
Пирамиды Объем наклонной призмы, пирамиды и конуса
Объем наклонной призмы, пирамиды и конуса Понятие цилиндра
Понятие цилиндра Перпендикуляр и наклонная
Перпендикуляр и наклонная Лист Мёбиуса
Лист Мёбиуса Рисунок «Бегемотик» на координатной плоскости
Рисунок «Бегемотик» на координатной плоскости