Содержание
- 2. Рассмотрим систему m линейных уравнений с n неизвестными:
- 3. Назовем матрицей системы матрицу, составленную из коэффициентов при неизвестных. Матрицу, полученную из А добавлением столбца свободных
- 4. Теорема Кронекера–Капелли Для того чтобы система линейных уравнений была совместной, необходимо и достаточно, чтобы ранг матрицы
- 5. Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение, если же ранг
- 6. Две системы, множества решений которых совпадают, называются эквивалентными или равносильными. Преобразование, применение которого превращает систему в
- 7. Пример Исследовать систему линейных уравнений
- 8. Составим расширенную матрицу системы и с помощью элементарных преобразований вычислим одновременно ранги обеих матриц.
- 9. Метод Гаусса Для того чтобы решить систему уравнений методом Гаусса выписывают расширенную матрицу этой системы и
- 10. Разрешается: 1) изменять порядок строк матрицы, что соответствует изменению порядка уравнений; 2) умножать строки на любые
- 11. С помощью этих преобразований каждый раз получается расширенная матрица новой системы, равносильной исходной, т. е. такой
- 12. Установить совместность и решить систему
- 13. Выпишем расширенную матрицу системы и поменяем местами первую и вторую строки для того, чтобы элемент равнялся
- 14. Прямой ход
- 16. Обратный ход Ранги матрицы системы и ее расширенной матрицы совпали с числом неизвестных. Согласно теореме Кронекера-Капелли
- 17. Имеем Далее, подставляя его в третье уравнение, найдем Подставляя и во второе уравнение, получим и, наконец,
- 18. Общее решение системы линейных уравнений Если ранг матрицы равен , то любой отличный от нуля минор
- 19. Пример Решить систему уравнений
- 20. Выпишем расширенную матрицу системы и преобразуем ее
- 21. Однородные системы
- 22. Теорема о совместности однородной системы Для того чтобы однородная система линейных уравнений имела нетривиальное решение, необходимо
- 23. При r Если m=n, т.е. число уравнений совпадает с числом неизвестных, матрица системы является квадратной. условие
- 24. Пример
- 25. Составим матрицу системы и методом элементарных преобразований найдем ее ранг.
- 26. r=2
- 27. Выберем в качестве базисного минор Тогда укороченная система имеет вид
- 28. Общее решение системы
- 29. Фундаментальная система решений Назовем фундаментальной системой решений систему матриц-столбцов, полученную из общего решения при условии, что
- 30. Матрицы-столбы, т.е. фундаментальную систему решений обозначают Е1, Е2, …, Еn. Общее решение будет представлено в виде
- 32. Скачать презентацию










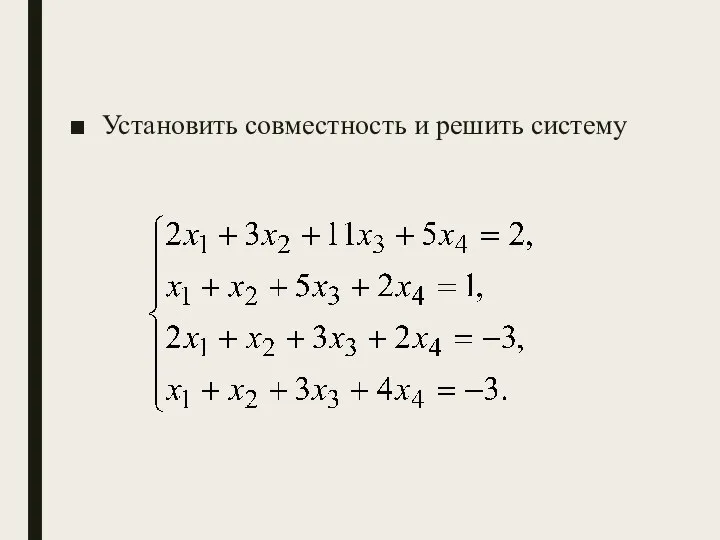


















 Презентация на тему Математический супертест
Презентация на тему Математический супертест  Презентация на тему Центральная и осевая симметрии в природе
Презентация на тему Центральная и осевая симметрии в природе  Длинный и короткий
Длинный и короткий Решение квадратных уравнений по формуле
Решение квадратных уравнений по формуле Числовые выражения
Числовые выражения Помоги ёжику. Интерактивный тренажёр по математике, 1 класс
Помоги ёжику. Интерактивный тренажёр по математике, 1 класс Определение производной. Правила вычисления производных. Таблица производных
Определение производной. Правила вычисления производных. Таблица производных Формулы сокращённого умножения
Формулы сокращённого умножения Решение задач на движение
Решение задач на движение Презентация на тему Отрезок. Графики
Презентация на тему Отрезок. Графики  Функция у = а (х -x0) +y0
Функция у = а (х -x0) +y0 Степень с целым показателем ( урок обобщения и систематизации в форме игры крестики – нолики)
Степень с целым показателем ( урок обобщения и систематизации в форме игры крестики – нолики) Числовые и буквенные выражения
Числовые и буквенные выражения Методы оценки рисков
Методы оценки рисков Особенности набора математических формул в Microsoft
Особенности набора математических формул в Microsoft Статистические оценки параметров распределения случайных величин по выборкам. Степенные средние
Статистические оценки параметров распределения случайных величин по выборкам. Степенные средние Занимательная математика
Занимательная математика Иррациональные уравнения. Открытый урок
Иррациональные уравнения. Открытый урок Что такое математика?
Что такое математика? Решение задач. Продолжи ряд чисел
Решение задач. Продолжи ряд чисел Выполните деление
Выполните деление Понятие о проценте. Урок формирования новых знаний
Понятие о проценте. Урок формирования новых знаний Обратная матрица
Обратная матрица Простейшие геометрические фигуры
Простейшие геометрические фигуры Геометрический и физический смысл производной, вычисление производной. 11 класс
Геометрический и физический смысл производной, вычисление производной. 11 класс Графический метод решения уравнений. Задания для устного счета
Графический метод решения уравнений. Задания для устного счета Числовая окружность в координатной плоскости
Числовая окружность в координатной плоскости Метод изучения длины
Метод изучения длины