Содержание
- 2. Тема 2:Логика высказываний
- 3. Лекция 4
- 4. Функциональная полнота систем логических функций
- 5. С.94-145
- 6. С.47-145
- 7. Логические функции одной и двух переменных называются элементарными где В – бинарное множество {0,1}
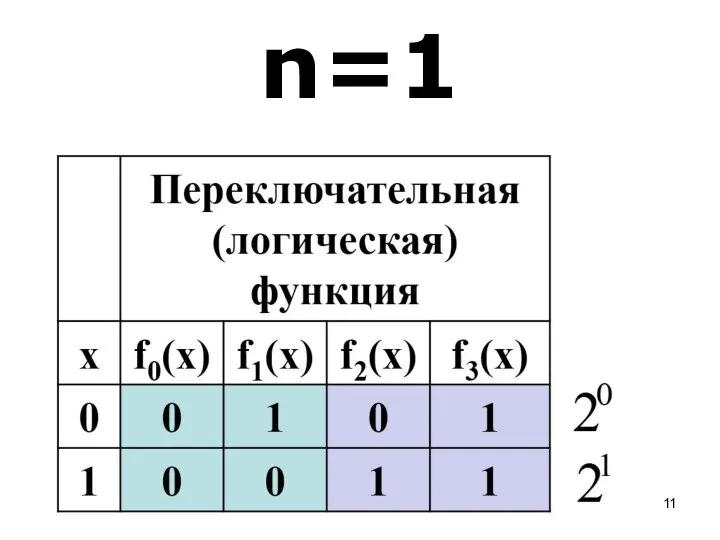
- 8. 1. Логические функции одной переменной
- 9. Сколько всего функций одной переменной?
- 10. 2⋅2
- 11. n=1
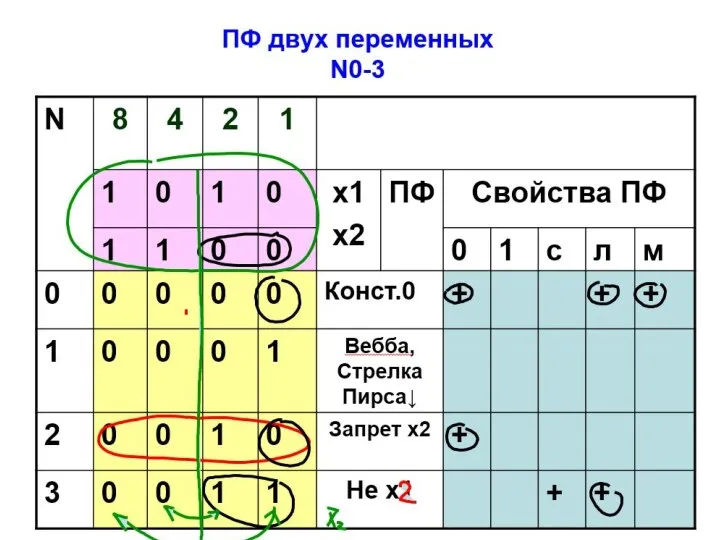
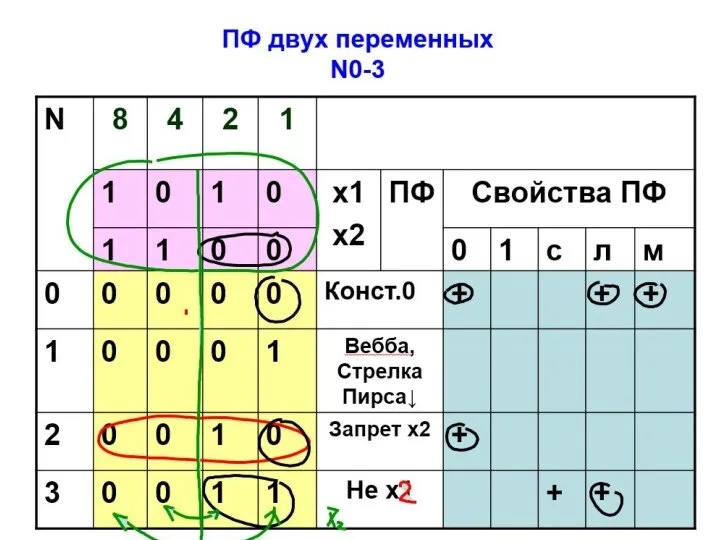
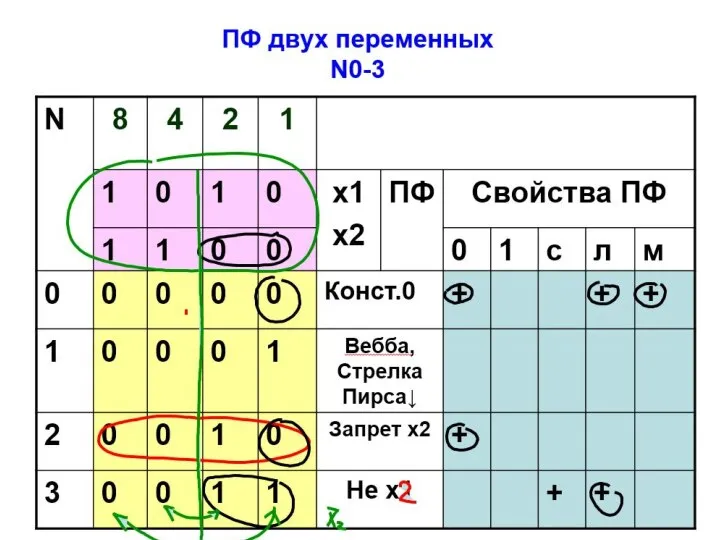
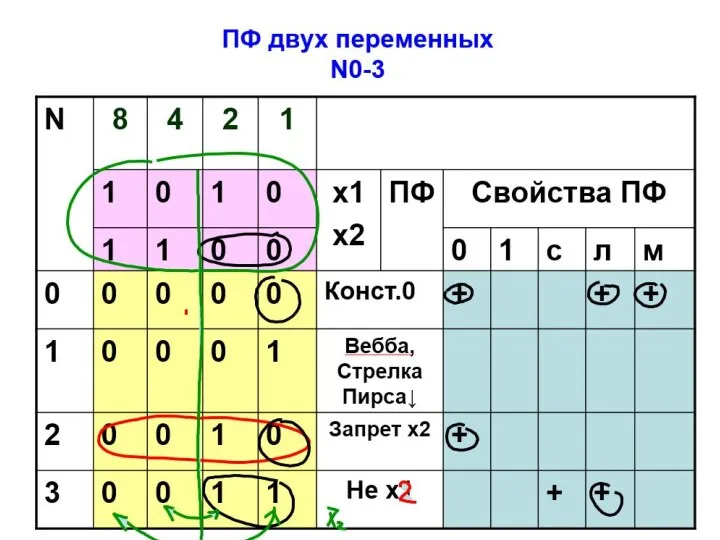
- 12. 2.Логические функции двух переменных
- 13. Сколько всего функций двух переменных?
- 14. 2⋅2⋅2⋅2
- 15. Сколько всего функций n переменных?
- 21. 3.Суперпозиция и проблема функциональной полноты
- 22. Суперпозиция Подстановка в данную функцию вместо ее переменных других функций.
- 23. Проблема функциональной полноты Каким должен быть минимальный состав элементарных логических функций, чтобы путём суперпозиции получить любую
- 24. Классы ПФ
- 25. 1) класс функций, сохраняющих константу 0. В этот класс входят функции, которые на нулевом наборе переменных
- 26. 2) класс функций, сохраняющих константу 1. В этот класс входят функции, которые на единичном наборе переменных
- 31. Самодвойственность
- 32. Двойственность f и g
- 33. Двойственность f и g
- 34. Самодвойственность
- 39. Линейность
- 40. Класс линейных функций. функция называется линейной, если возможно представление в виде линейного полинома, использующего функцию сложения
- 41. f(x1x2)=с0⊕с1х1⊕с2х2
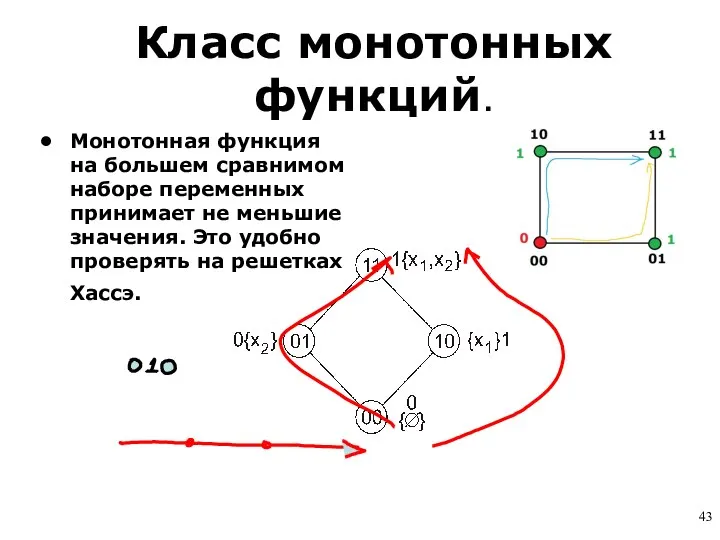
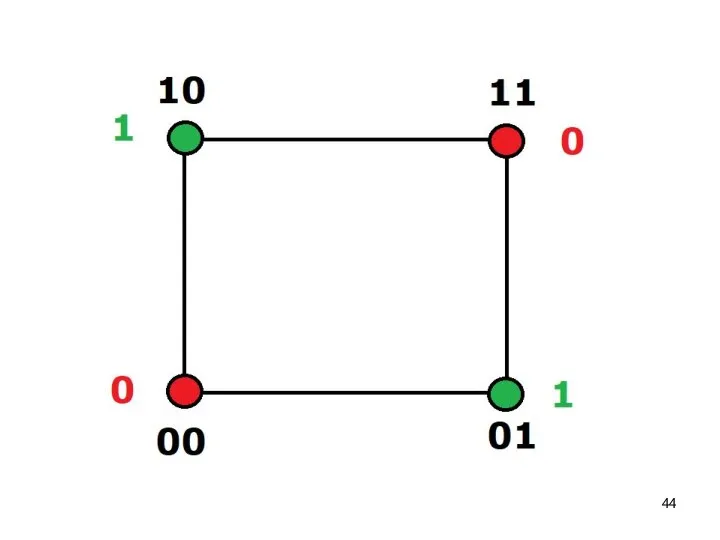
- 42. Монотонность
- 43. Класс монотонных функций. Монотонная функция на большем сравнимом наборе переменных принимает не меньшие значения. Это удобно
- 51. 3.Теорема (критерий) Поста
- 52. Пост, Эмиль Леон (1897 – 1954)
- 53. Система функций называется функционально полной, если любая произвольная переключательная функция от любого числа переменных может быть
- 54. для функциональной полноты систем логических функций необходимо и достаточно, чтобы они содержали следующие функции: не сохраняющую
- 55. Функционально полные системы переключательных функций представляют собой базис. Всего можно получить 17 различных минимальных базисов из
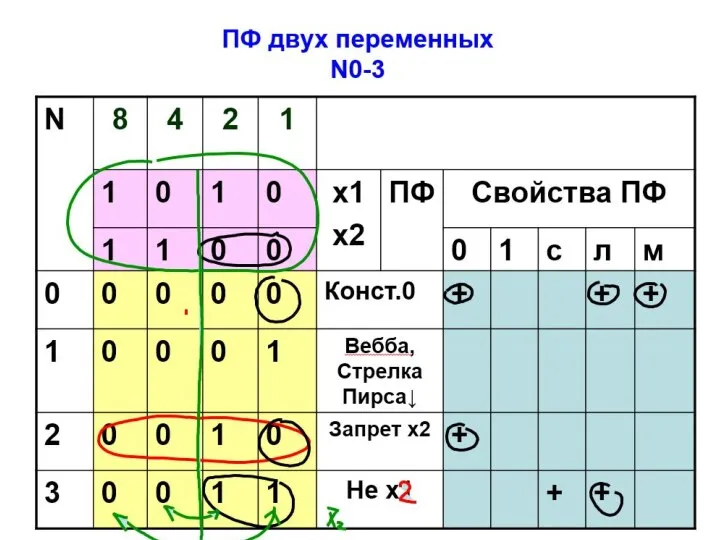
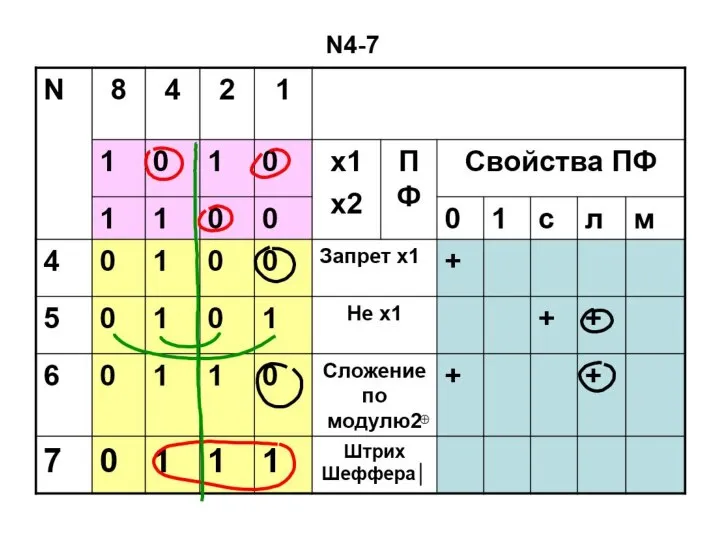
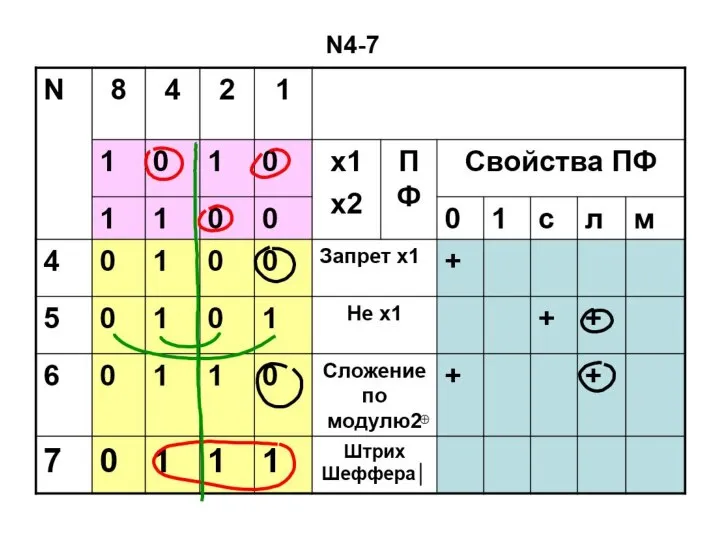
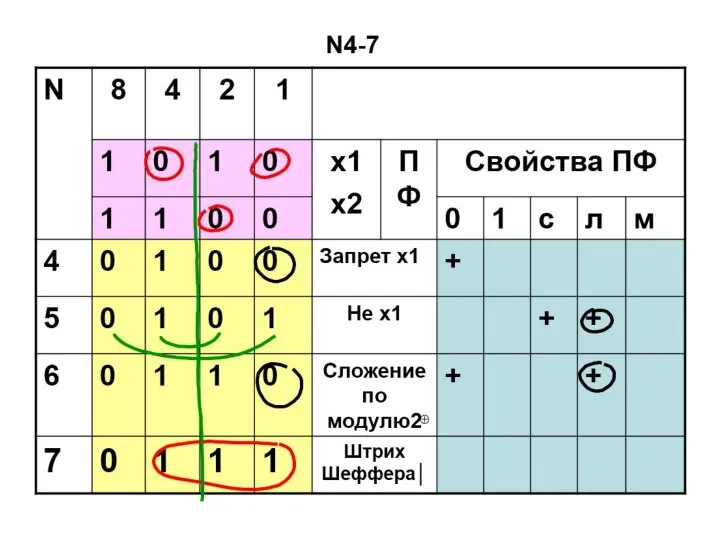
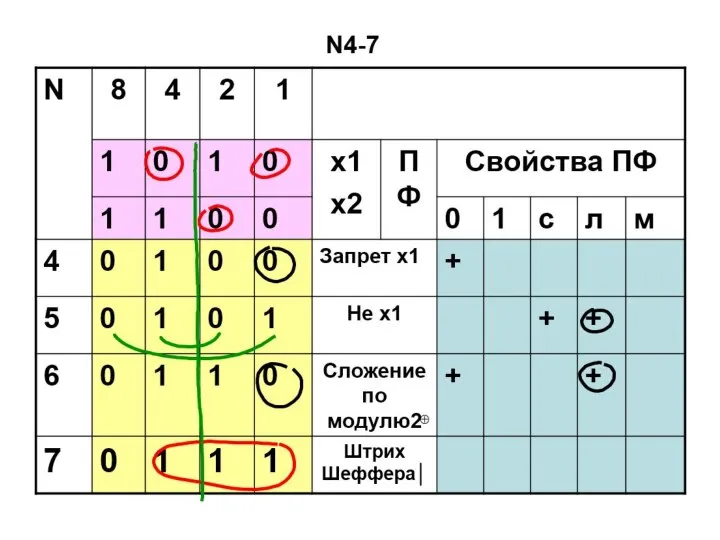
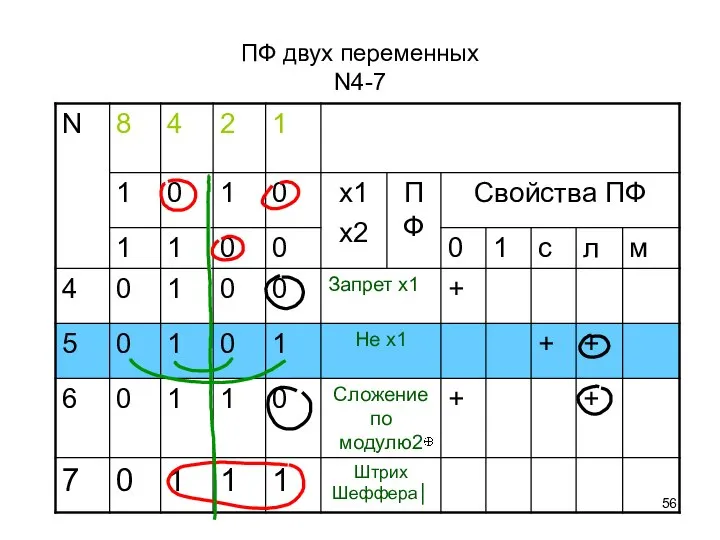
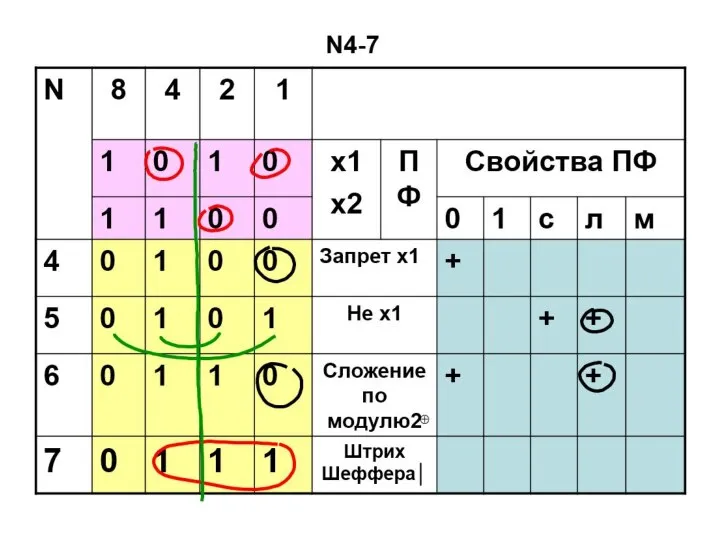
- 56. ПФ двух переменных N4-7
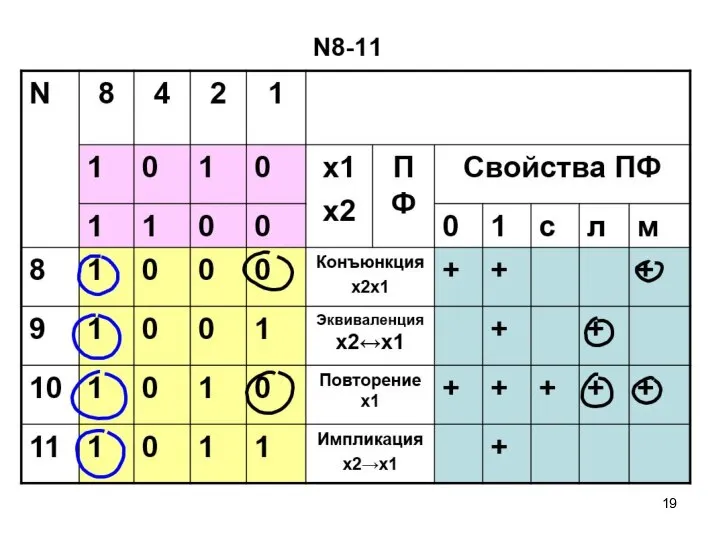
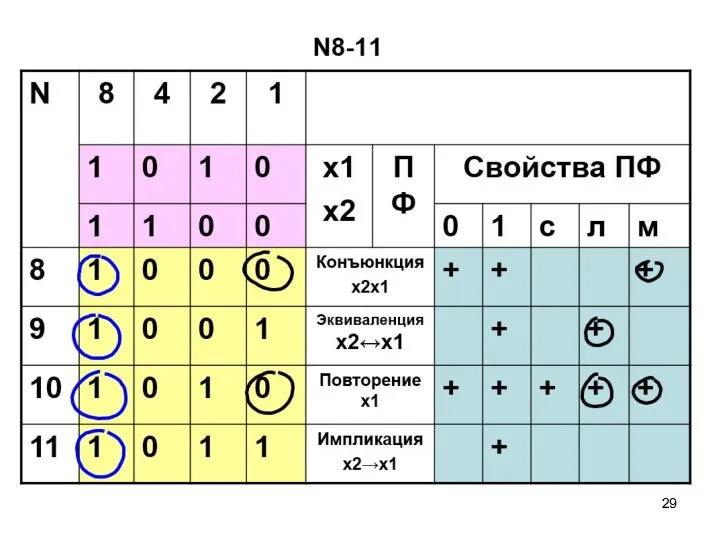
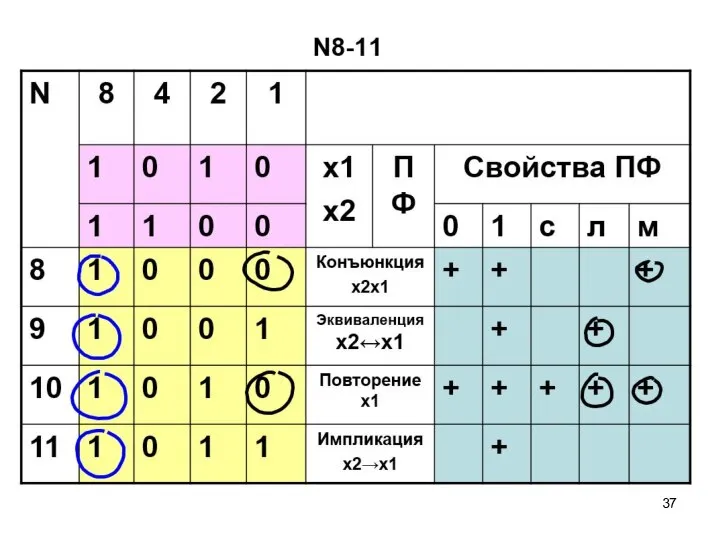
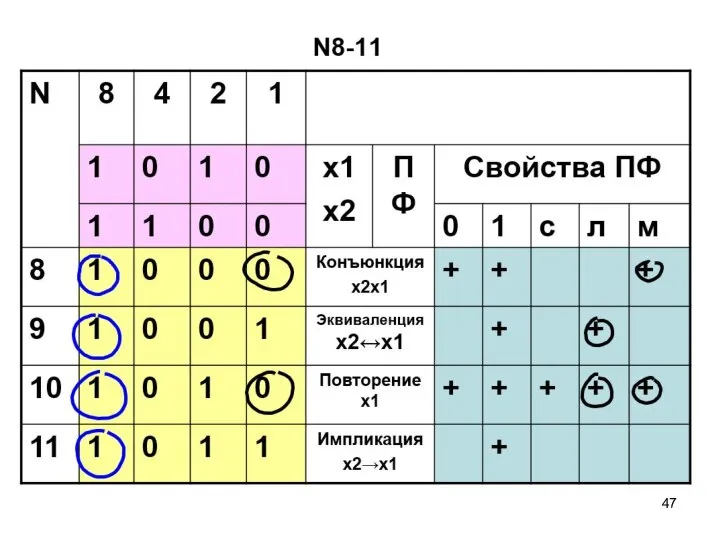
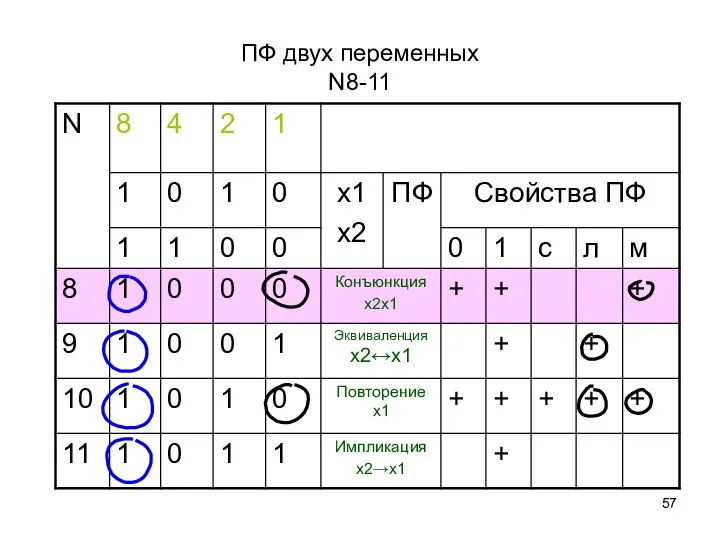
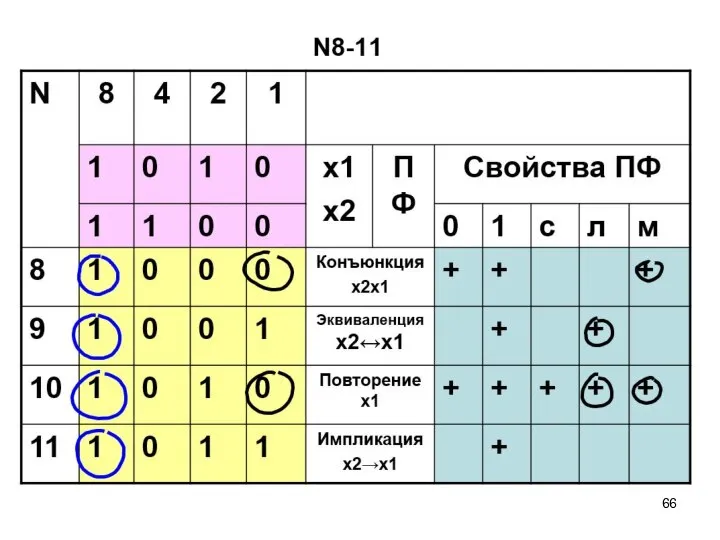
- 57. ПФ двух переменных N8-11
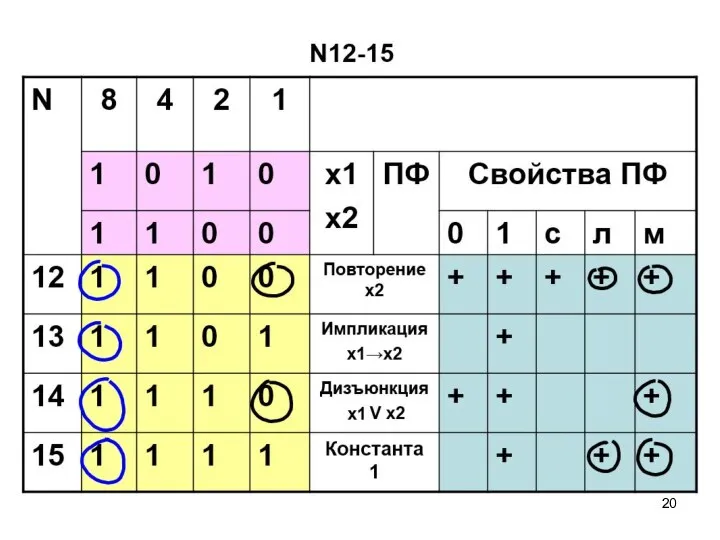
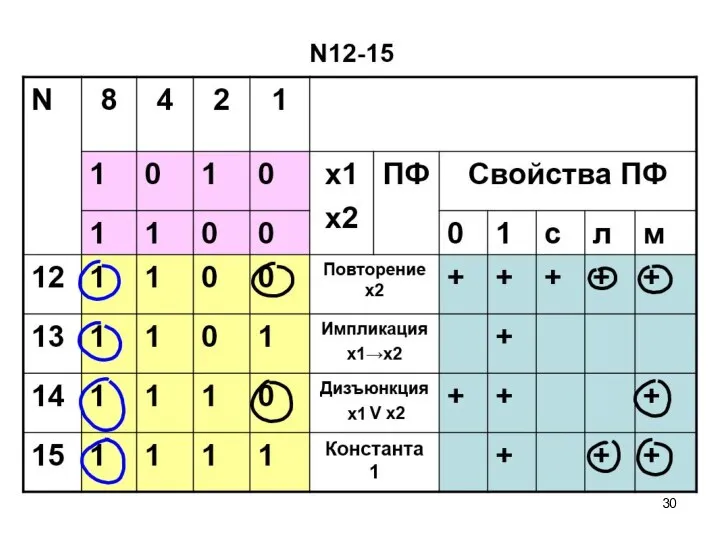
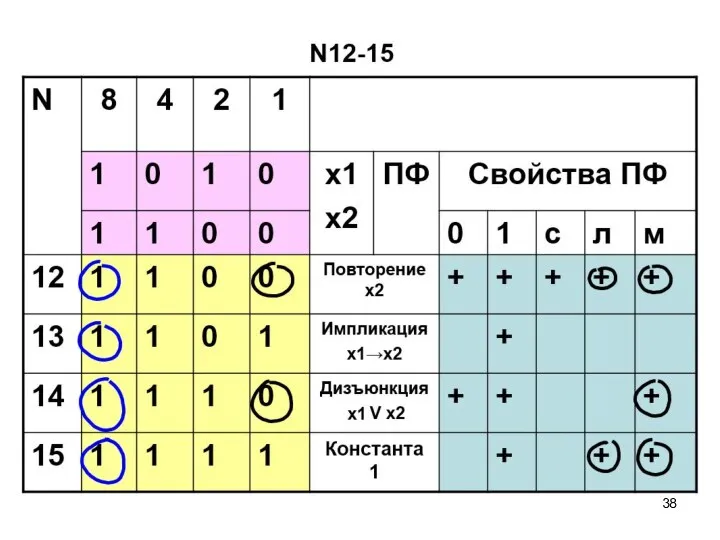
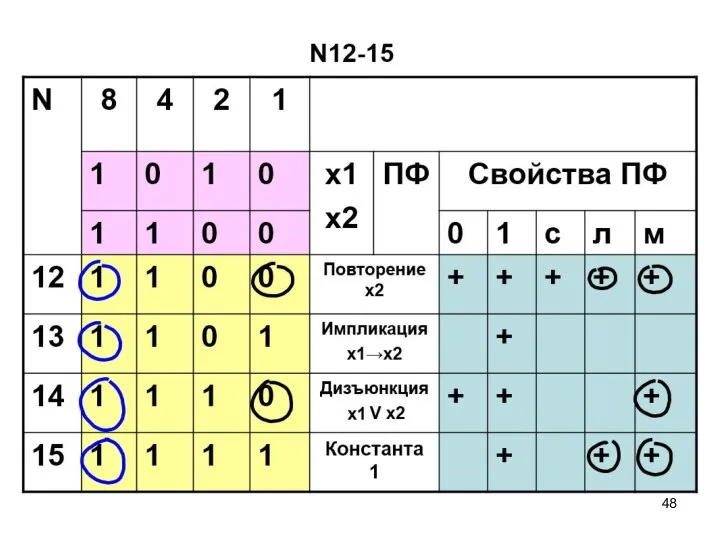
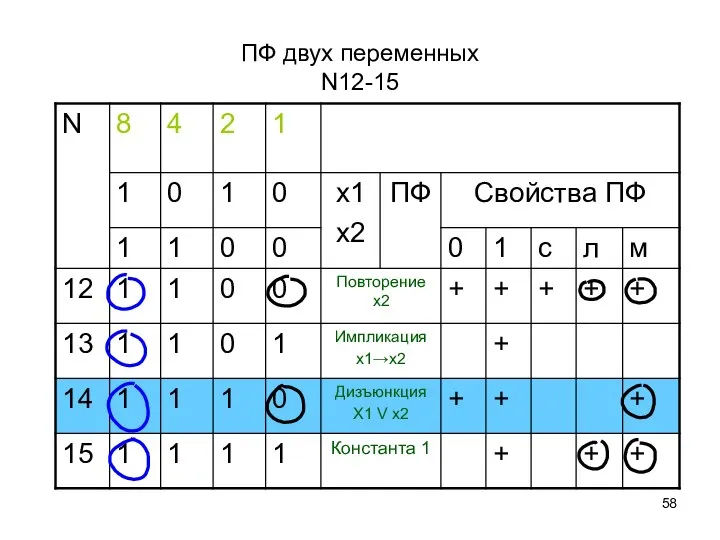
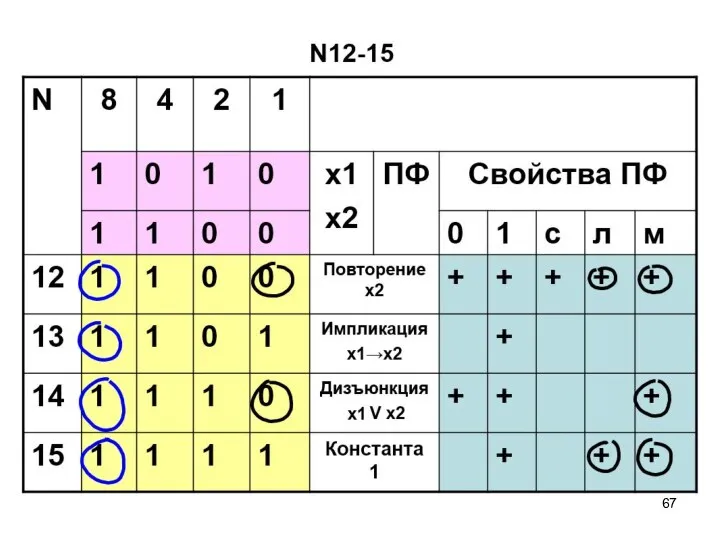
- 58. ПФ двух переменных N12-15
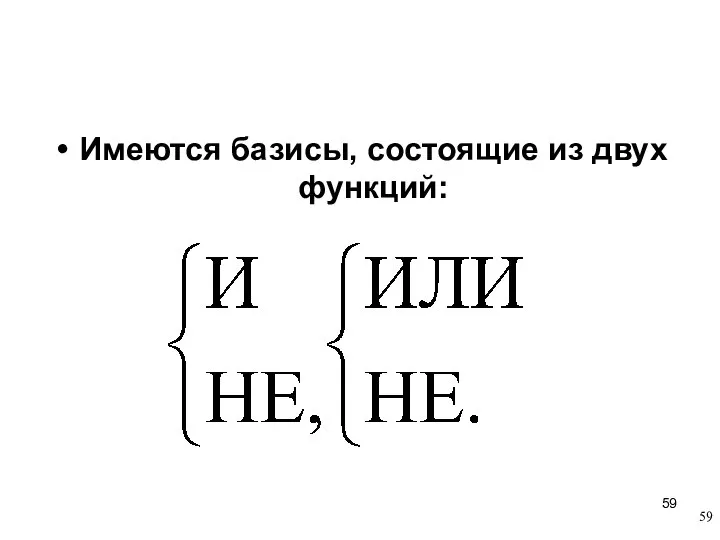
- 59. Имеются базисы, состоящие из двух функций:
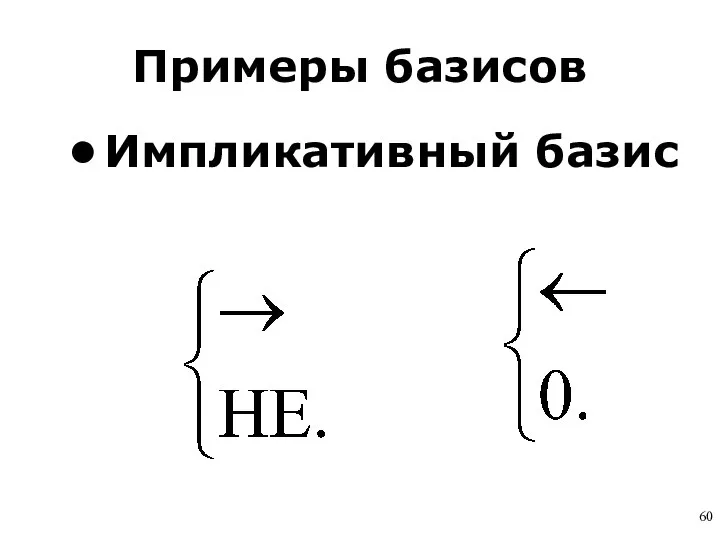
- 60. Примеры базисов Импликативный базис
- 61. Примеры базисов Базис Жегалкина:
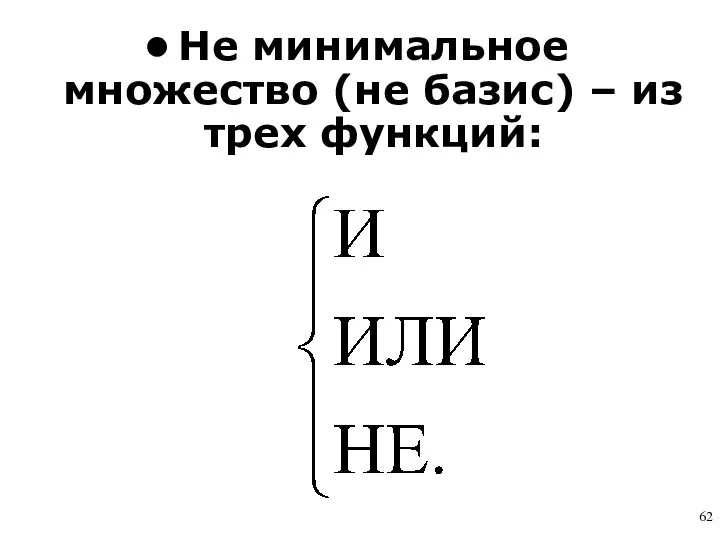
- 62. Не минимальное множество (не базис) – из трех функций:
- 63. Имеются функции, обладающие всеми пятью отмеченными свойствами. Таковы функции↓⎥. Часто их называют соответственно ИЛИ-НЕ, И-НЕ. Таким
- 68. Т3. МИНИМИЗАЦИЯ ФОРМУЛ ЛОГИКИ ВЫСКАЗЫВАНИЙ
- 69. С.118-145
- 70. С.62-102
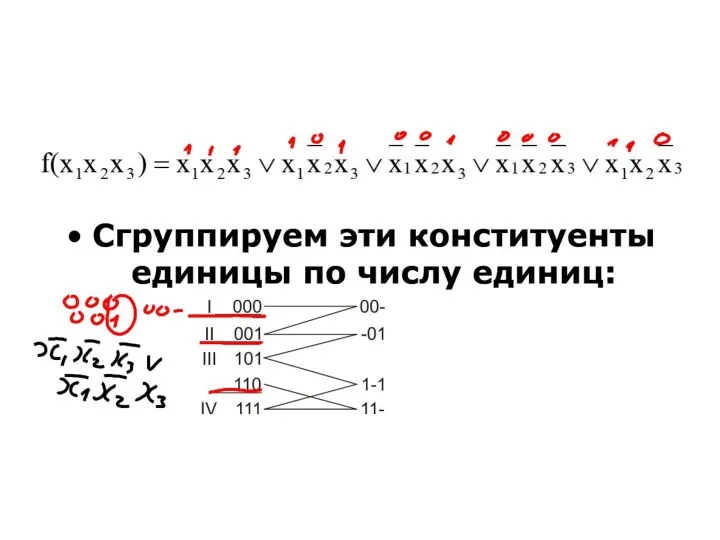
- 71. Метод Квайна-Мак-Класки.
- 72. Willard Van Orman Quine (1908-2000), McCluskey (1929-2016)
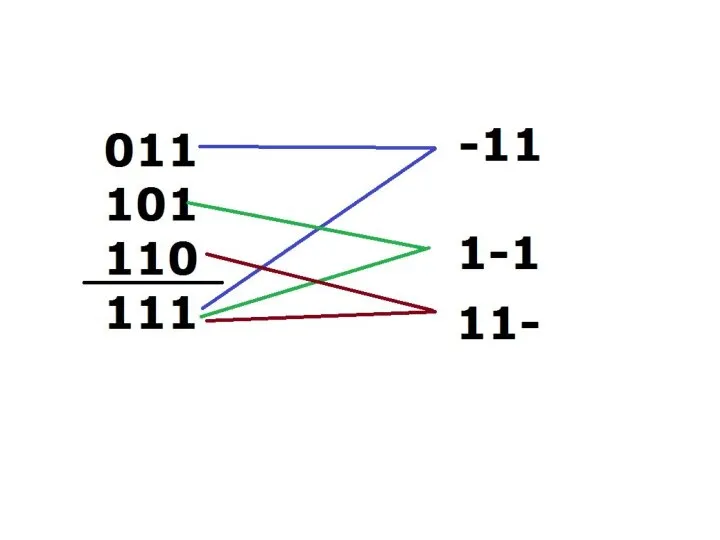
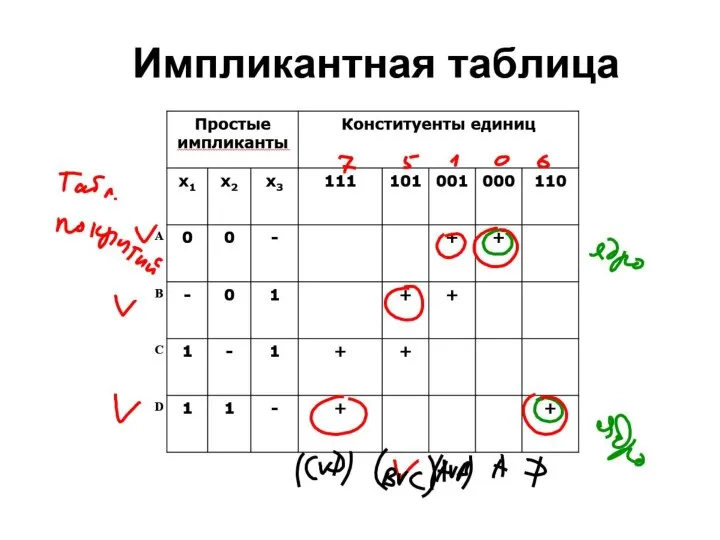
- 75. Таблица Квайна
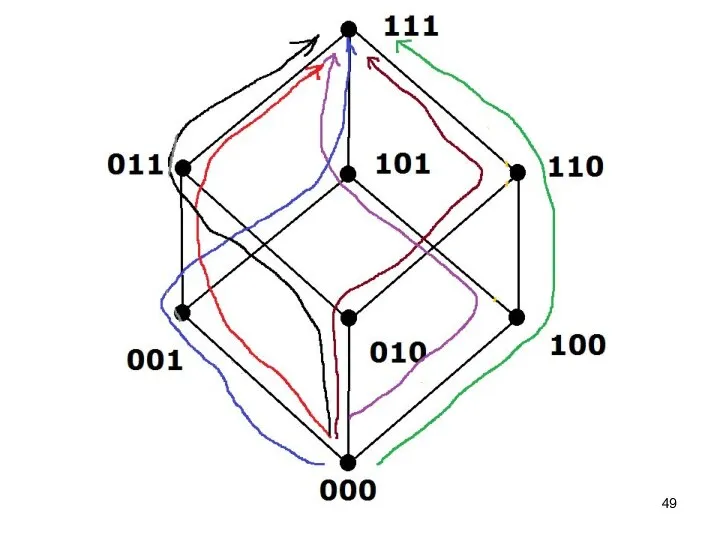
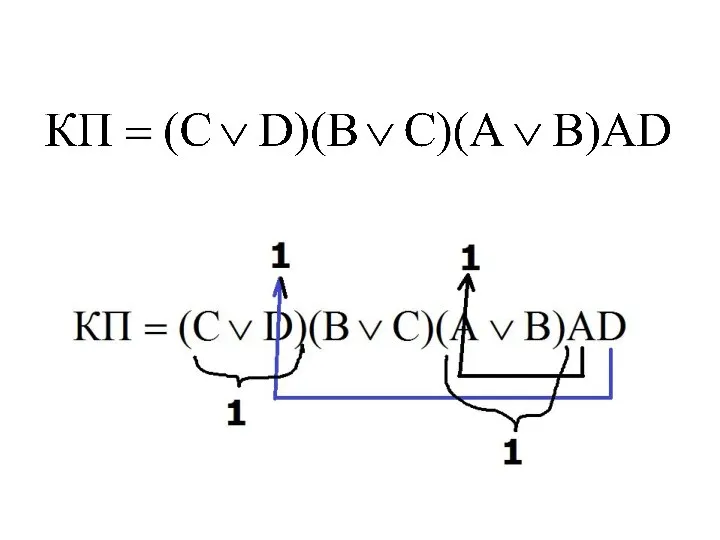
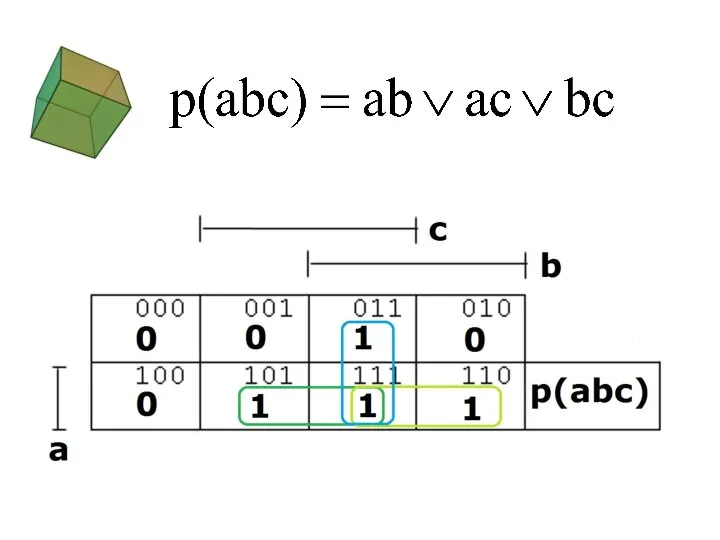
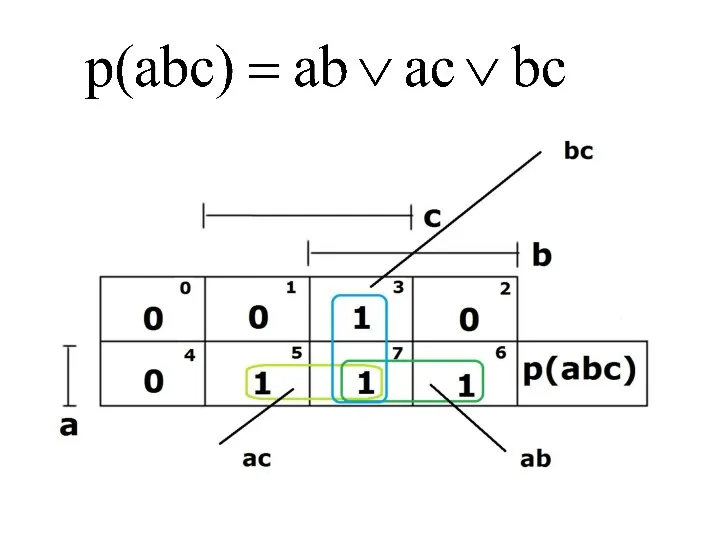
- 81. Минимизация по кубу соседних чисел
- 89. МИНИМИЗАЦИЯ ПО КАРТАМ КАРНО
- 91. Maurice Karnaugh (1924) is an American physicist, famous for the Karnaugh mapMaurice Karnaugh (1924) is an
- 92. Edward W. Veitch (1924 –2013) was an American computer scientist.
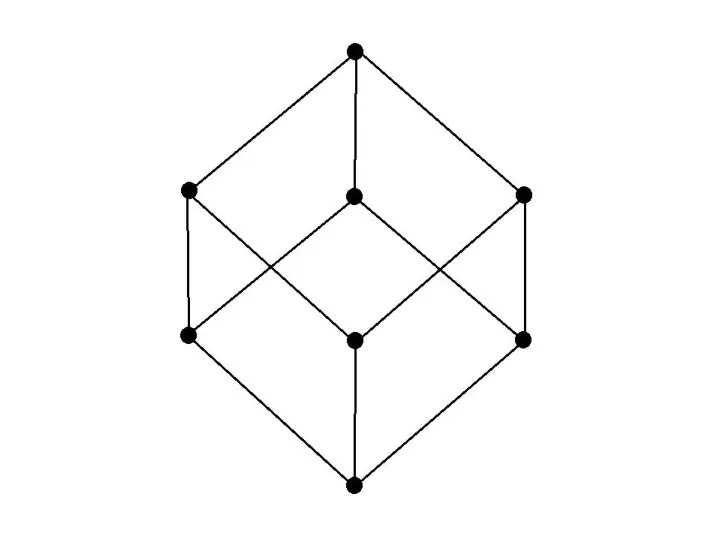
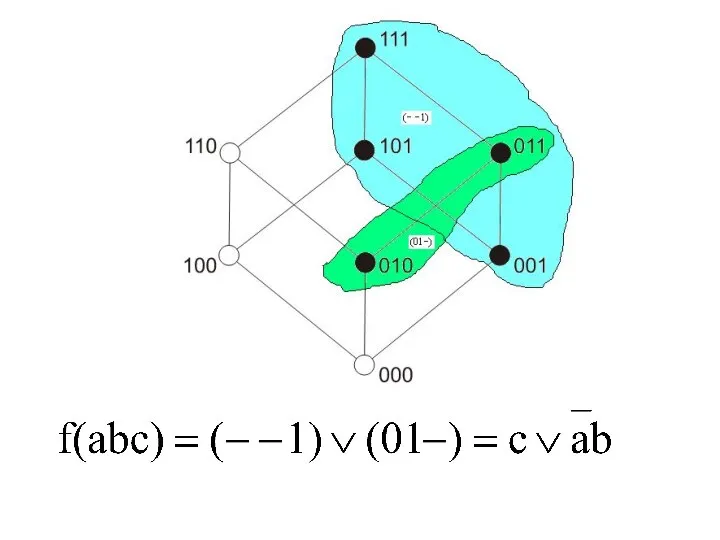
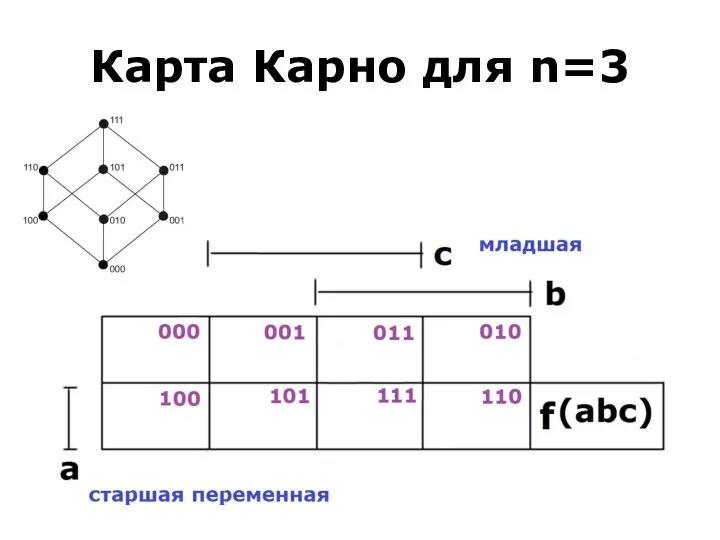
- 93. Карта Карно для n=3
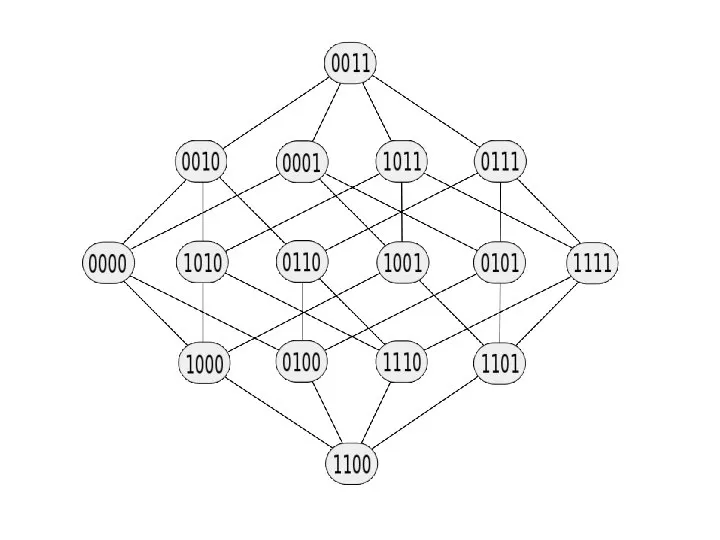
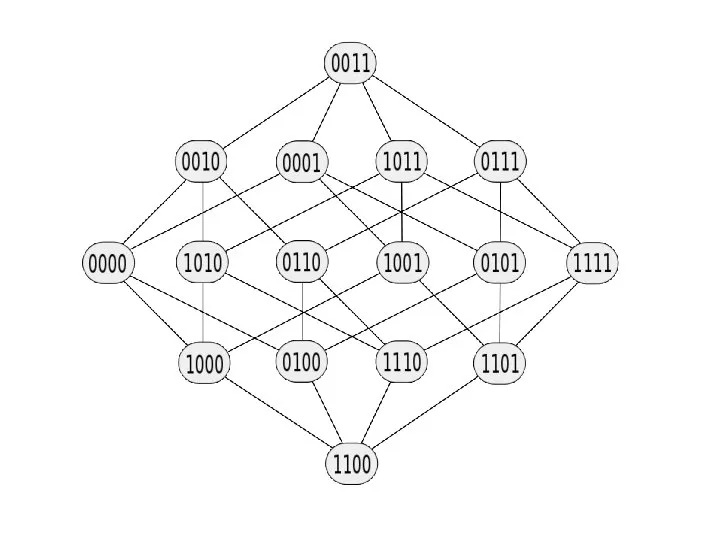
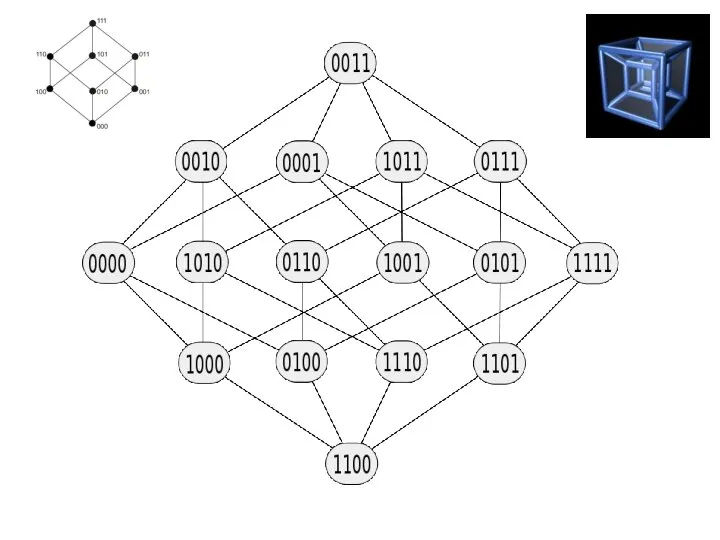
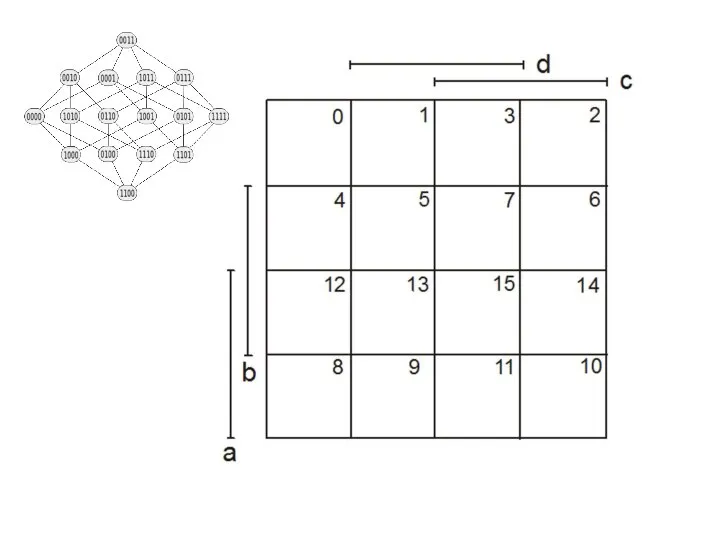
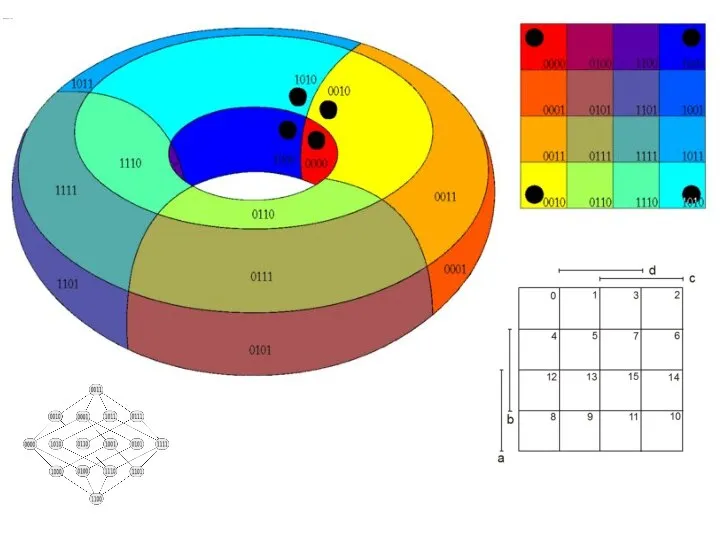
- 97. Карта Карно для n=4
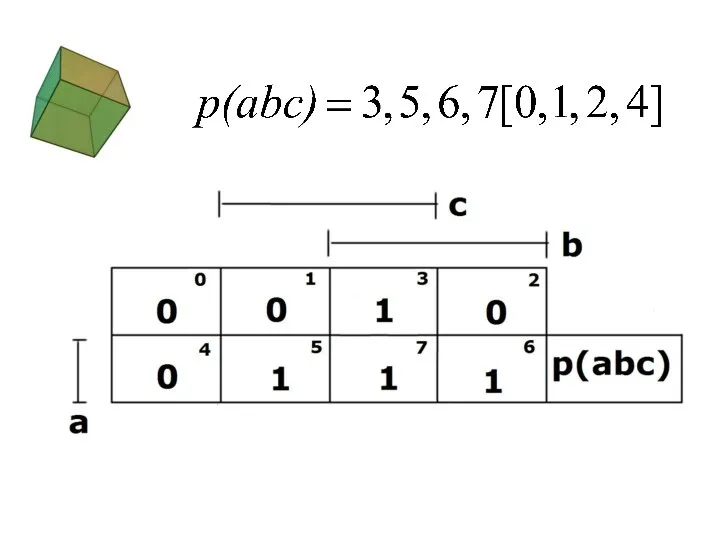
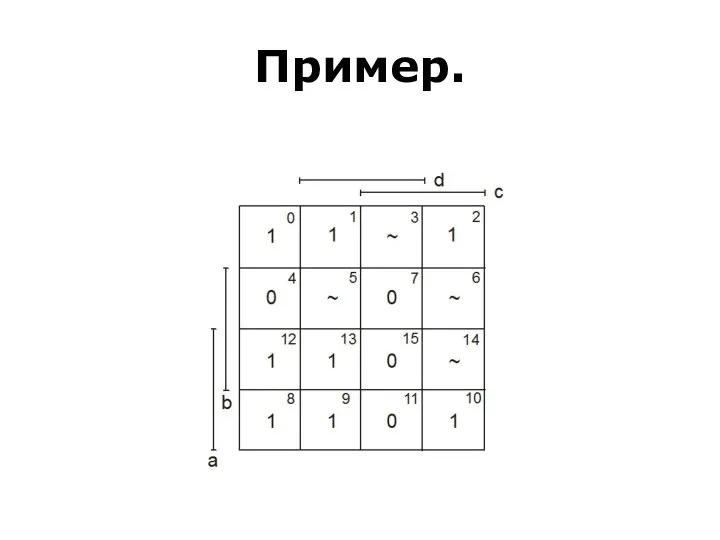
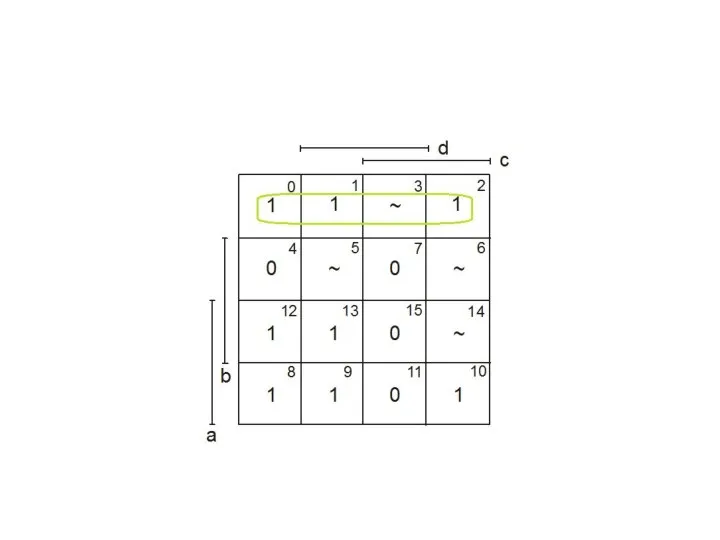
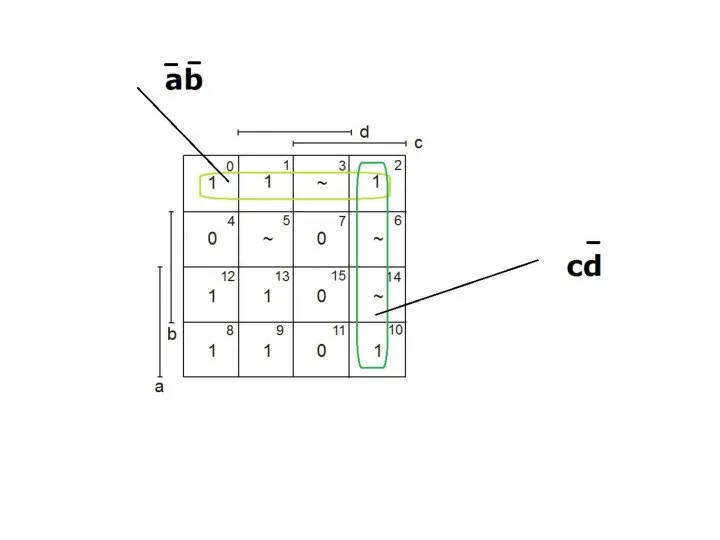
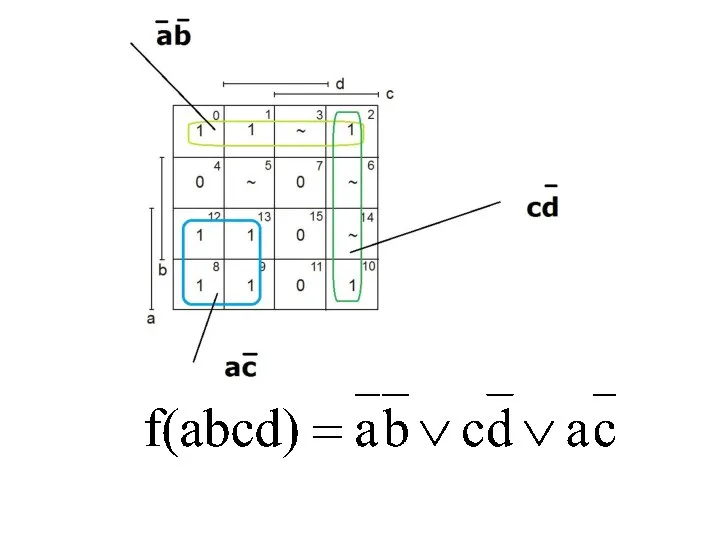
- 101. Пример.
- 105. Карта Карно для n=5?
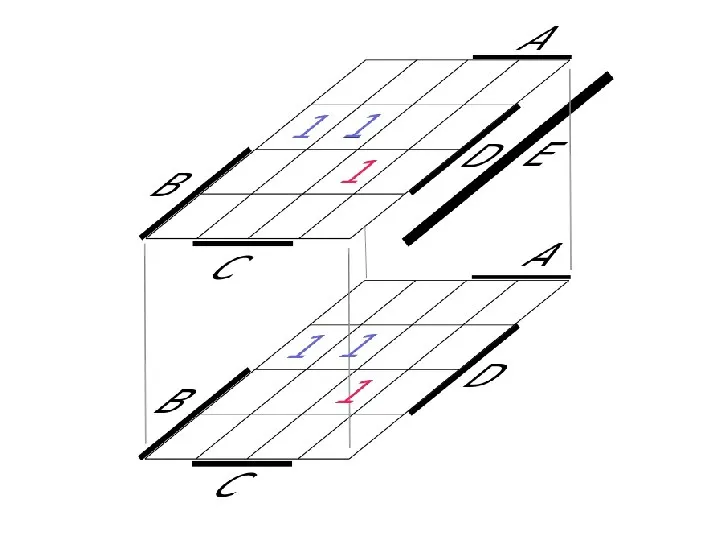
- 107. Карта Карно для n=6?
- 110. Скачать презентацию











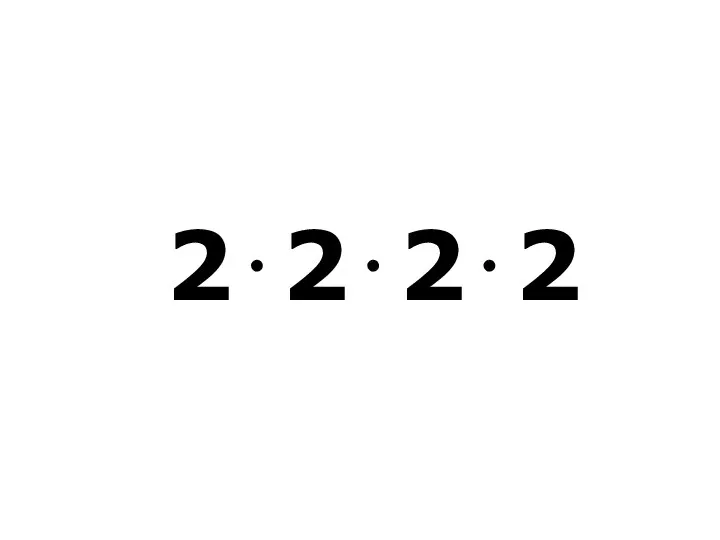

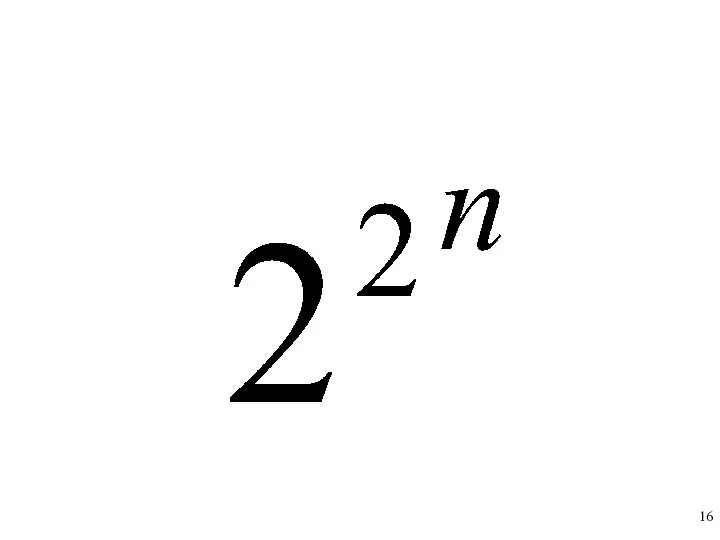







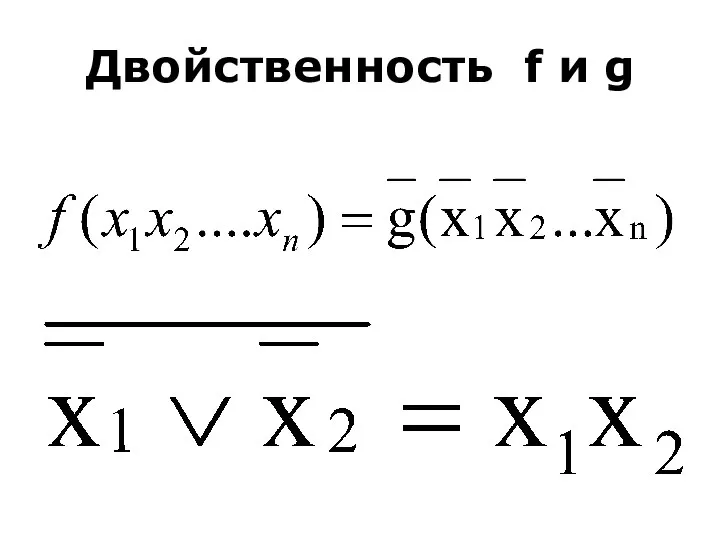
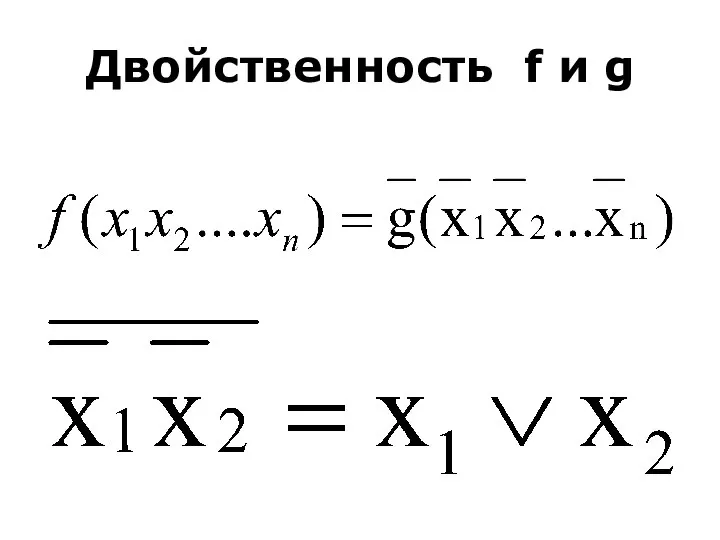
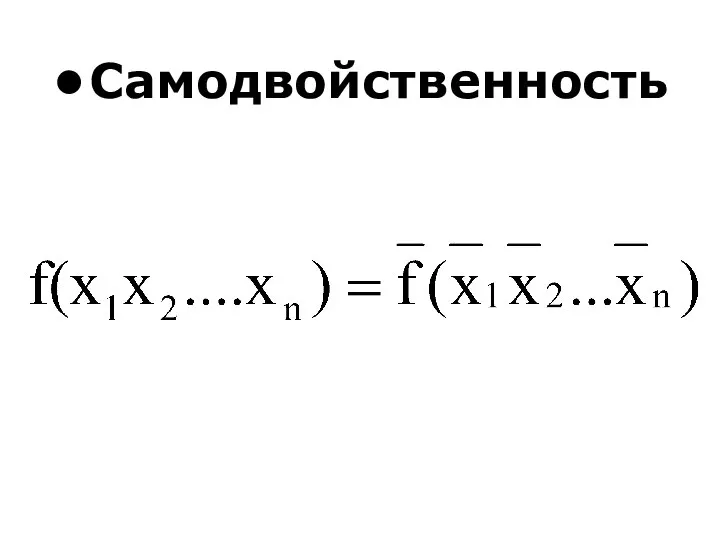
















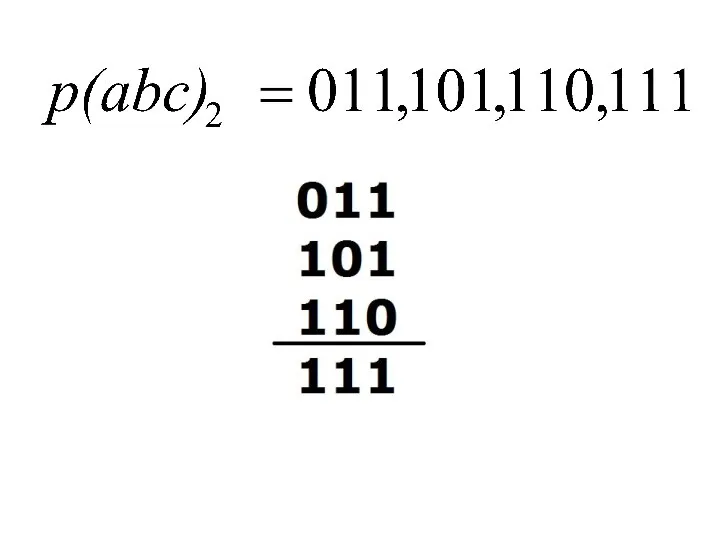

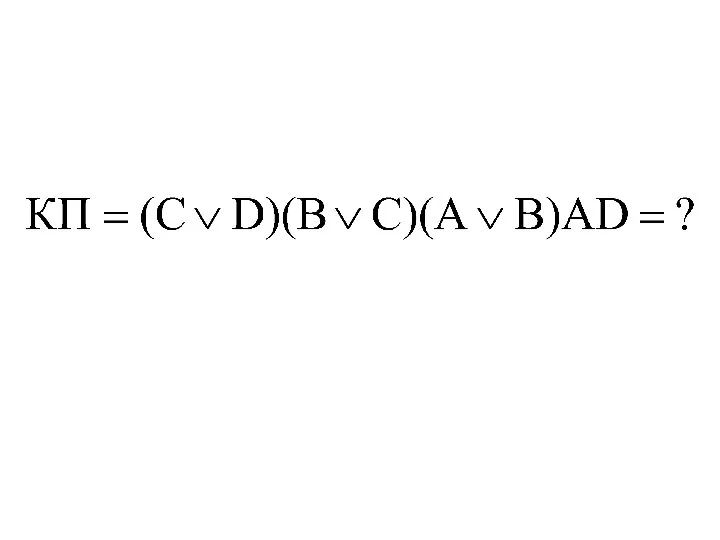
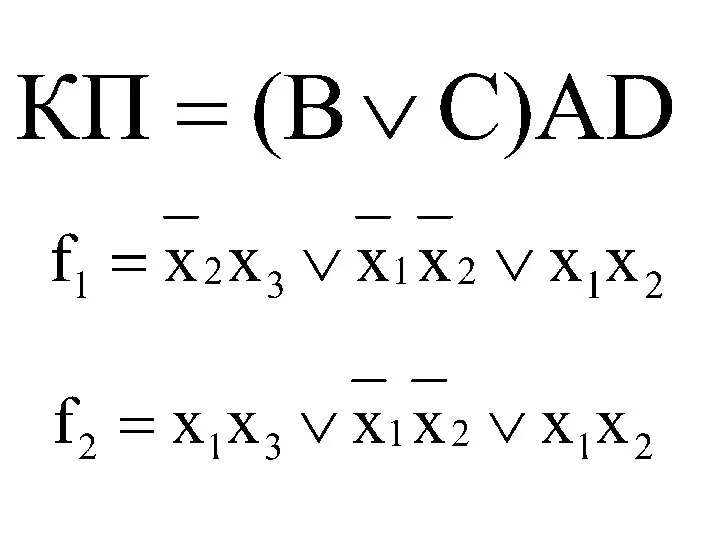










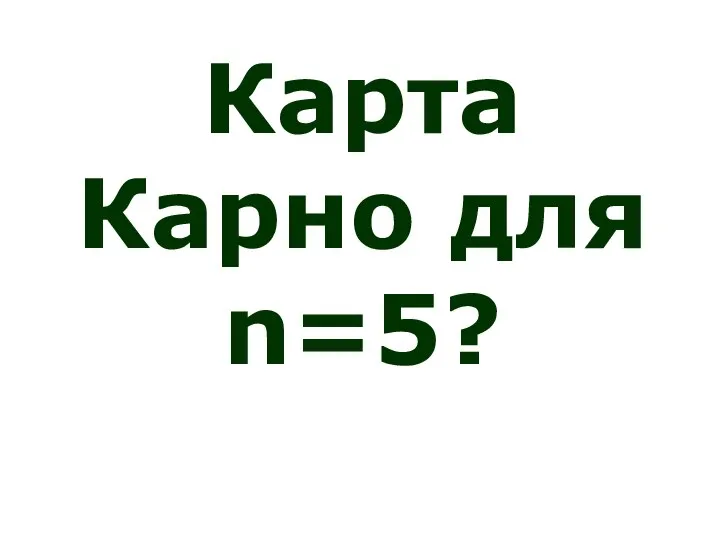


 иррациональные_уравнения_2
иррациональные_уравнения_2 Игра Счастливый случай. Внеклассное мероприятие по математике
Игра Счастливый случай. Внеклассное мероприятие по математике Расположение прямой и окружности
Расположение прямой и окружности Второй признак равенства треугольников. Геометрия , 7 класс
Второй признак равенства треугольников. Геометрия , 7 класс Решение задач на проценты
Решение задач на проценты Цилиндр
Цилиндр Десятки, единицы, цифры
Десятки, единицы, цифры Комбинаторика. 11 класс
Комбинаторика. 11 класс Цилиндр
Цилиндр SLUChAJNYE_VELIChINY
SLUChAJNYE_VELIChINY Центральная симметрия
Центральная симметрия Треугольник. Периметр треугольника. 9 класс
Треугольник. Периметр треугольника. 9 класс Построение треугольника по трём элементам с помощью циркуля и линейки
Построение треугольника по трём элементам с помощью циркуля и линейки Сложение и вычитание чисел
Сложение и вычитание чисел Организация экспериментов с использованием системных принципов
Организация экспериментов с использованием системных принципов Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Инвариант. Решение олимпиадных задач
Инвариант. Решение олимпиадных задач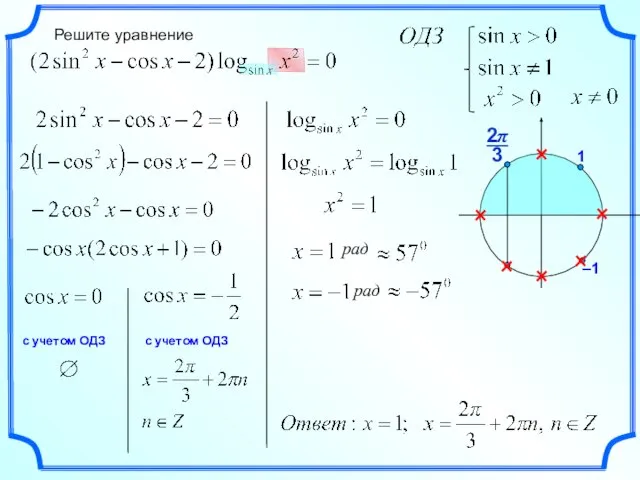 Решение уравнения
Решение уравнения Множественные связи. Порядковые и категоризованные переменные
Множественные связи. Порядковые и категоризованные переменные Окружность, круг, их элементы и части. Центральный угол
Окружность, круг, их элементы и части. Центральный угол Сложение чисел (1 класс)
Сложение чисел (1 класс) Средняя линия треугольника
Средняя линия треугольника Тригонометрия. Математическая игра АС-11
Тригонометрия. Математическая игра АС-11 Лінійка — найпростіший прилад для вимірювання довжини
Лінійка — найпростіший прилад для вимірювання довжини Корреляционный анализ в Exel
Корреляционный анализ в Exel Куб. Формулы для куба
Куб. Формулы для куба Параллельность прямых. Урок – практикум
Параллельность прямых. Урок – практикум Симметрия в искусстве
Симметрия в искусстве